Position et trajectoire

Vecteur position

Vecteur position: Définition

Important

Vecteur position

On définit la position d’un point matériel M dans un référentiel \(\mathfrak{R}\) à l’aide du vecteur position \(\overrightarrow{OM}\) où O est un point fixe du référentiel.

Type de représentation

On peut être amené à tracer des trajectoires en utilisant la représentation paramétrique (coordonnées en fonction d’un même paramètre, le temps) ou cartésienne (une coordonnée cartésienne en fonction d’un autre) ou polaire (une coordonnée polaire en fonction d’une autre).

Important

Equation horaire et trajectoire

L’évolution du mouvement du point matériel \(\overrightarrow{OM}(t)\) est appelée équation horaire. Elle est aussi définie par les composantes du vecteur position dans la base de projection. La courbe paramètrée (ou trace) ainsi définie est appelée trajectoire.

Expression du vecteur position

Il arrive qu’on puisse éliminer la variable temps pour obtenir des équations cartésiennes \(y(x)\) ou polaire (\(r(\theta)\)).

On trouvera très souvent la notation \(r\) au lieu de \(r\) pour désigner la variable radiale en coordonnées cylindriques ou polaires. Attention, elle ne représente pas la même grandeur qu’en sphérique.

Important

Expressions

On peut exprimer le vecteur position dans les différents repères. Les vecteurs des bases locales sont exprimées au point M mobile:

• Coordonnées cartésiennes: \(x_M(t) \overrightarrow{e_x} + y_M(t) \overrightarrow{e_y} + z_M(t) \overrightarrow{e_z}\).

• Coordonnées cylindrique: \(r_M(t) \overrightarrow{e_r} + z_M(t) \overrightarrow{e_z}\).

• Coordonnées sphériques: \(r_M(t) \overrightarrow{e_r}\).

Attention

On rappelle que les bases cylindriques et sphériques sont des bases locales dont les vecteurs vont varier lorsque le point M se déplace. Il faudra donc tenir compte de leur dérivées temporelles :

• Coordonnées cylindrique: \(r_M(t) \overrightarrow{e_r}(\theta(t)) + z_M(t) \overrightarrow{e_z}\).

• Coordonnées sphériques: \(r_M(t) \overrightarrow{e_r}(\theta(t), \phi(t))\).

Trajectoires usuelles

Trajectoire rectiligne

Un trajectoire rectiligne ne signifie pas que le mobile va toujours dans le même sens. Il peut rebrousser chemin.

Important

Mouvement rectiligne

Un mouvement rectiligne est un mouvement dont la trajectoire est portée par une droite (ou un segment) fixe dans le référentiel d’étude. Il se fait suivant une direction de l’espace: c’est un mouvement à 1 degré de liberté.

Choix du système de coordonnées

En général, on prévoit par une étude physique que le mouvement sera rectiligne. On va donc choisir un système de coordonnées cartésiennes (ou à la limite cylindriques) dont un axe est confondu avec le support de la trajectoire.

Trajectoire circulaire

Important

Mouvement circulaire

Un mouvement est dit circulaire si le point M se déplace sur un cercle (ou une portion de cercle) fixe dans le référentiel R. C’est aussi un mouvement à 1 degré de liberté.

Choix du système de coordonnées

On va donc choisir un système de coordonnées cylindriques (ou polaires) de centre O le centre du cercle et d’axe Oz perpendiculaire au plan du cercle. On étudiera plus en détail les caractéristiques d’un tel mouvement.

Equation cartésienne et paramétrique

On peut être amené à obtenir une trajectoire circulaire sans l’avoir prévu et en ayant utilisé au départ des coordonnées cartésiennes. Il est important de reconnaître qu’une équation cartésienne ou paramétrique est l’équation d’un cercle.

Ainsi, si l’on peut mettre le couple de coordonnées cartésiennes \((x(t);y(t))\) sous la forme:

\[\begin{align*} x(t) = R \cos \omega t + x_0\\ y(t) = R \sin \omega t + y_0 \end{align*}\]

Et on peut aussi écrire l’équation d’un cercle sous la forme:

(1)\[\begin{equation}\label{eq_cercle_cartesienmtex_234} {(x - x_0)}^2 + {(y - y_0)}^2 = R^2 \end{equation}\]

Dans les deux cas, il s’agit de l’équation d’un cercle de rayon R et de centre C dont les coordonnées sont \(C(x_0,y_0)\)

Trajectoire elliptique

On fera attention au fait que le centre du repère ne définit pas le même point particulier de l’ellipse suivant qu’on utilise les coordonnées cartésiennes ou polaires.

Important

Ellipse

Une ellipse est une courbe fermée qu’on peut caractériser/reconnaître de plusieurs manières:

• Lieu géométrique (peu usité en physique): Soit deux points, appelées foyers, \(F_1\) et \(F_2\) et un réel positif K, l’ensemble des points M tel que \(MF_1 + MF_2 = K\) décrit une ellipse. Le milieu du segment \(F_1 F_2\) est appelé centre de l’ellipse.

• Représentation polaire (fondamentale): Soit un point F centre d’un repère polaire. L’ensemble des points M dont les coordonnées du vecteur position \(\overrightarrow{FM}\) sont tels que \(r = \frac{p}{1 + e \cos{(\theta - \theta_0)}}\) avec \(p > 0\) et \(0 \leq e < 1\) décrit une ellipse. Le point F est un des foyers de l’ellipse. On dit que p est le paramètre de l’ellipse et que e est l’excentricité de l’ellipse.

• Représentation cartésienne (très utile). L’ensemble des M dont les coordonnées \((x,y)\) sont telles que: \({(\frac{x}{a})}^2 + {(\frac{y}{b})}^2 = 1\) décrit une ellipse dont le centre est le centre du repère.

• Représentation paramétrique (utile): L’ensemble des M dont les coordonnées \((x(t) = a \cos t ; y(t) = b \sin(t))\) décrit une ellipse dont le centre est le centre du repère.

Caractéristiques d’une ellipse.

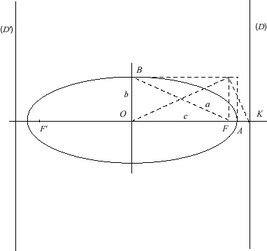
Les caractéristiques utiles sont:

• le demi-grand axe a (=OA)

• le demi-petit axe b (=OB)

• la distance focale c (=OF)

Trajectoire parabolique

Orientation

Dans le cas polaire, si \(\theta_0 = 0\) (cas fréquent) l’axe de symétrie de la parabole est l’axe qui sert d’origine des angles, soit en général l’axe Ox. Ce qui est différent du cas cartésien présenté ici.

Important

Parabole

Une parabole est une courbe non fermée qu’on peut caractériser/reconnaître de plusieurs manières:

• Représentation polaire (fondamentale): Soit un point F centre d’un repère polaire. L’ensemble des points M dont les coordonnées du vecteur position \(\overrightarrow{FM}\) sont tels que \(r = \frac{p}{1 + e \cos{\theta - \theta_0}}\) avec \(p > 0\) et \(e = 1\) décrit une parabole. Le point F est appelé foyer de la parabole. On dit que p est le paramètre de la parabole et que e est l’excentricité de la parabole.

• Représentation cartésienne (très utile). L’ensemble des M dont les coordonnées \((x,y)\) sont telles que: \(y = ax^2 + bx + c\) décrit une parabole d’axe de symétrie parallèle à Oy.

Coniques

Définition

Les coniques correspondent à l’ensemble des courbes qu’on peut obtenir par l’intersection d’un cône et d’un plan. Il en résulte trois types de conique:

• l’ellipse

• la parabole

• l’hyperbole

Important

Equation polaire d’une conique

En choisissant correctement l’origine du repère polaire, on peut exprimer l’équation polaire d’une conique sous la forme:

\[ r(\theta) = \frac{p}{1 \pm e \cos \left(\theta - \theta_0\right)} \]

Le centre du repère est alors appelée foyer de la conique. A noter que l’ellipse et la parabole possède deux foyers symétriques par rapport au centre de la conique (centre de symétrie de la conique).

p est appelée paramètre de l’ellipse et e excentricité. En changeant l’origine des angles, on peut faire en sorte de \(\theta_0 = 0\).

De nombreuses propriétés seront vues sur les coniques lors du cours sur les potentiels newtoniens. On retiendra déjà que la valeur de l’excentricité déterminer le type de conique:

• ellipse: \(0 \leq e < 1\)

• parabole: \(e = 1\)

• hyperbole: \(e > 1\). Attention, en coordonnées polaires, les asymptotes sont en général obliques.