Entrainement

Pendule simple modifié

On considère un pendule simple modifié. Un mobile ponctuel M de masse m est accroché à l’extrémité d’un fil inextensible de longueur L et de masse négligeable, dont l’autre extrémité est fixe en O. On néglige tout frottement. On repère la position du pendule par l’angle \(\theta\) qu’il fait avec la verticale. Lorsque \(\theta>0\), le système se comporte comme un pendule simple de centre O et de longueur de fil L. A la verticale et en dessous de O, un clou planté en O’ avec OO’=L/3, qui bloquera la partie haute du fil vers la gauche. Quand \(\theta < 0\), le système se comporte donc comme un pendule simple de centre O’ et de longueur de fil 2L/3.

A la date t=0, le mobile est lâché sans vitesse initiale avec une inclinaison \(\theta(0) = \theta_0 > 0\). On note \(t_1\) la date de première rencontre du fil avec le clou et \(t_2\) la date de la première annulation de la vitesse du mobile pour formule. L’intervalle \([0; t_1[\) est nommé première phase du mouvement, l’intervalle \(]t_1;t_2[\) est nommé deuxième phase du mouvement. A la date \(t_1^{-}\), le fil n’a pas encore rencontré le clou et à la date \(t_1^{+}\), le fil vient de toucher le clou.

1. Par le théorème de la puissance mécanique (dérivée du théorème de l’énergie mécanique), établir l’équation différentielle vérifiée par \(\theta\) pour la première phase du mouvement.

2. En utilisant le théorème de l’énergie mécanique, déterminer la vitesse \(v_1^{-}\) de M à la date \(t_1^{-}\). En déduire la vitesse angulaire \(\omega_1^{-}\) à cette date.

3. Dans l’hypothèse des petites oscillations (pour cette question uniquement), déterminer la durée \(\delta t_I\) de la première phase.

4. Le blocage de la partie supérieure du fil par le clou ne s’accompagne d’aucun transfert énergétique. Déterminer la vitesse \(v_1^{+}\) de M à la date \(t_1^{+}\). En déduire la vitesse angulaire \(\omega_1^{+}\) à cette date.

5. Déterminer l’angle \(\theta_2\) atteint à l’instant \(t_2\).

6. On se place à nouveau dans le cadre des petites oscillations. En utilisant les résultats des questions 1 et 2, donner sans calcul la durée \(\delta t_{II}\) de la deuxième phase.

7. Décrire brièvement la suite du mouvement de ce système et donner l’expression de sa période T.

Point utile pour cet exercice

• \(\Longrightarrow\) Système conservatif.

• \(\Longrightarrow\) Théorème de l’énergie cinétique.

• \(\Longrightarrow\) Pendule aux petits angles.

Mouvement d’un anneau sur une piste

On considère le dispositif suivant où un objet assimilable à un point matériel M de masse m se déplace solidairement à une piste de deux parties circulaires de rayons \(R_1\) et \(R_2\) et de centres \(C_1\) et \(C_2\) dans un plan vertical. On repère la position de M par l’angle \(\theta\) dont le centre de référence est soit \(C_1\) (partie (1)), soit \(C_2\) (partie (2)). On prend les angles croissants dans le sens trigonométrique et \(\theta_A=- \pi/2\). Il n’y a pas de frottements et on note g l’accélération de la pesanteur.

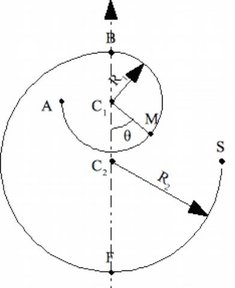
1. Exprimer l’énergie potentielle de pesanteur \(E_p(\theta)\) de M en supposant \(E_p = 0\) au point \(B(\theta = \pi)\). On distinguera les cas (1) et (2).

2. Tracer l’allure de \(E_p(\theta)\)

3. Déterminer les positions angulaires d’équilibre et leur stabilité.

4. L’anneau est initialement en A. Il est lancé avec une vitesse \(V_0\) (dans le sens trigonométrique).

   1. Montrer graphiquement qu’on doit imposer une condition sur la vitesse \(V_0\) pour que le mobile M atteignent le point F.

   2. Exprimer cette condition en fonction des données du problème.

   3. En déduire la vitesse du mobile en F (notée \(V_F\)) quand cette condition est remplie.

   4. La condition précédente remplie, l’anneau sort-il de la piste en S? A quelle vitesse (notée \(V_S\))?

5. Déterminer à chaque instant la valeur de l’accélération normale en fonction de V la vitesse du mobile et des rayons \(R_1\) et \(R_2\) pour chaque partie (1) et (2).

6. Dans la partie (1), déterminer la réaction de la piste sur l’anneau. S’il était remplacé par une bille roulant à l’intérieur de la piste, quelle serait la condition sur formule pour que la bille reste sur la piste.

7. Même question pour la partie (2).

Point utile pour cet exercice

• \(\Longrightarrow\) Système conservatif.

• \(\Longrightarrow\) Théorème de l’énergie mécanique.

• \(\Longrightarrow\) Barrière de potentiel.

• \(\Longrightarrow\) Position d’équilibre et stabilité.

Eléments de réponse (sans justification)

\[\begin{align*} &\begin{cases} E_p( \theta \leq \pi) &= -mgR_1 (\cos \theta + 1)\\ E_p( \theta \geq \pi) &= -mgR_2 (\cos \theta + 1) \end{cases} & V_0 \geq \sqrt{2 g R_1}\\ & V_S = \sqrt{V_{0}^2 - 2gR_1 + 2gR_2} & N = \frac{mV_0^2}{R_{1}} + 3mg \cos \theta > 0 \end{align*}\]

Equilibre de charges et petits mouvements

Tous les mouvements ont lieu suivant l’axe Ox et on néglige l’effet du poids. La force électrostatique exercée par un point \(M_1\) de charge \(q_1\) sur un point \(M_2\) de charge \(q_2\) est: \(\overrightarrow{f} = \frac{q_1 q_2}{4 \pi \epsilon_0 M_1 M_2^2} \overrightarrow{u}\) où \(\overrightarrow{u}\) est un vecteur unitaire dirigé de \(M_1\) vers \(M_2\). On travaille dans un référentiel R supposé galiléen.

1. Un point matériel de charge \(q\) est fixé en O, origine du repère. Un autre point matériel M de charge identique \(q\), initialement à droit de O, à la distance \(a\) de O, est abandonné sans vitesse initiale.

   1. Déterminer en fonction de \(x=OM>0\), l’énergie potentielle associée à la force électrostatique subie par M. On la prendra par convention nulle pour M à l’infini.

   2. Le point M est-il dans un état lié ou de diffusion?

   3. Déterminer la vitesse du point M lorsqu’il est à l’infini.

2. Un autre point matériel fixe O’ de charge 4q est ajouté à une distante 2a à droite de O. Le point M est placé entre O et O’.

   1. Déterminer vectoriellement la résultante des forces qui s’exerce sur M en fonction de x=OM (\(0<x<2a\)). En déduire la position d’équilibre. On la notera par la suite \(x_0\).

   2. Déterminer l’expression de l’énergie potentielle \(E_p(x)\) du point et étudier la stabilité de la position d’équilibre \(x_0\) pour 0 < x < 2a.

   3. Représenter l’allure de \(E_p(x)\) pour la particule de charge q pour \(x \in [0; 2a]\). Calculer la valeur de l’extremum \(E_p(x_0)\).

3. On lâche sans vitesse initiale la particule M (de charge q, masse m) au voisinage du point d’équilibre.

   1. Justifier qu’on puisse faire l’approximation \((x - x_0) \ll 1\) pour tout le mouvement.

   2. Etablir l’équation différentielle du mouvement au voisinage de cette position

   3. En déduire la pulsation des petites oscillations et la forme de \(x(t)\).

Point utile pour cet exercice

• \(\Longrightarrow\) Système conservatif.

• \(\Longrightarrow\) Théorème de l’énergie mécanique.

• \(\Longrightarrow\) Position d’équilibre et stabilité.

Eléments de réponse (sans justification)

Cas à une charge: \(E_p(x) = \frac{q^2}{4\pi \epsilon_0 x}\)

\(v_{\infty}^2 = \frac{q^2}{2\pi \epsilon_0 m a}\)

Cas à deux charges: \(E_p(x) = \frac{q^2}{4 \pi \epsilon_0} \left ( \frac{1}{x} + \frac{4}{2a - x}\right)\)

Position d’équilibre (stable): \(x_{eq} = \frac{2a}{3}\)

\(\omega_0 = \sqrt{\frac{\frac{q^2}{4 \pi \epsilon_0}\frac{81}{8a^3}}{m}}\)

Bille accrochée à deux ressorts

On considère le mouvement d’une bille M de masse m pouvant coulisser sans frottement sur un cerceau de plan vertical, de centre O et de rayon R. On note AB le diamètre horizontale du cerceau, Ox l’axe horizontal, Oy l’axe vertical et \(\theta\) l’angle entre Ox et OM. Le sens trigonométrique est pris positif (on suppose que \(\theta_B = 0\)). On suppose que le cerceau est fixe dans le référentiel du laboratoire supposé galiléen. Dans tout le problème, on prendra comme origine des potentiels le point le plus bas du cerceau.

1. Dans un premier temps, la bille est attachée à un ressort de longueur à vide nulle et de raideur k dont la seconde extrémité est fixée en B.

   1. Faire un bilan des forces qui s’appliquent sur la bille M. Quelles sont les forces qui travaillent?

   2. Déterminer l’expression de la longueur du ressort en fonction de R et \(\theta\). En déduire l’expression de l’énergie potentielle élastique pour le point M.

   3. Déduire du théorème de l’énergie mécanique l’équation différentielle du mouvement.

   4. Déterminer à partir de l’équation différentielle les position d’équilibre et étudier leur stabilité par linéarisation de l’équation. On note \(\theta_d\) la position d’équilibre pour \(\theta \in [- \pi; 0]\).

   5. Retrouver les conclusions précédentes par une étude de l’énergie potentielle.

2. Dans la suite, en plus du ressort précédent, on attache la bille à un deuxième ressort identique au premier mais dont la seconde extrémité est fixée en A.

   1. Faire un bilan des forces qui s’appliquent sur la bille M. Quelles sont les forces qui travaillent?

   2. Déterminer l’expression de la longueur du second ressort en fonction de R et \(\theta\). En déduire l’expression de l’énergie potentielle élastique du le point M pour le second ressort.

   3. Exprimer le théorème de l’énergie cinétique (forme locale) pour le point M. En déduire l’équation différentielle du mouvement. Qu’observe-t-on?

   4. Déterminer la résultante des forces de rappel élastique et justifier l’observation précédente.

   5. Déterminer les positions d’équilibre et étudier leur stabilité.

   6. Déterminer l’expression de la réaction \(\overrightarrow{N}\) du cerceau en fonction de \(\theta\) sachant qu’on abandonne la bille depuis \(\theta = \theta_0\) sans vitesse initiale. (On supposera \(\vert \theta_0 \vert \approx \pi/2\)).

   7. En déduire la condition à vérifier pour que la bille quitte le cerceau.

   8. Quelle est la condition nécessaire sur \(k, R, m, g\) pour que la bille reste sur le cerceau lorsqu’elle est à l’équilibre.

Point utile pour cet exercice

• \(\Longrightarrow\) Système conservatif.

• \(\Longrightarrow\) Ressort.

• \(\Longrightarrow\) Théorème de l’énergie mécanique.

• \(\Longrightarrow\) Position d’équilibre et stabilité.

Eléments de réponse (sans justification)

Un ressort:

\(E_p = -k R^2 {(\cos{\theta})} - mgR\sin \theta + mgR\)

Positions d’équilibre: \(\tan \theta = \frac{mgR}{kR^2}\), il n’y a qu’une position stable: \(\theta_{eq} = \arctan \frac{mgR}{kR^2}\)

Deux ressorts:

\(E_p = -mgR \sin\theta + mgR\), la seule position d’équilibre est en \(\pi/2\)