Exercices d’application

Ces exercices d’application directe sont à faire à la suite du cours pour vérifier votre compréhension des méthodes. Vous pourrez confronter votre travail avec celui de vos camarades et poser des questions sur cet exercice en classe mais il ne sera pas donné de correction complète.

Vecteur vitesse

Retrouver les expressions du vecteur vitesse dans les différents systèmes de coordonnées en dérivant directement le vecteur position exprimés dans ces systèmes.

Chute d’une règle

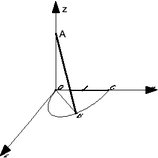
Une barre rectiligne AB de longueur fixe \(2b\) se déplace dans le référentiel R repéré par \((O, \overrightarrow{u_x},\overrightarrow{u_y},\overrightarrow{u_z})\) de telle sorte que:

• son extrémité A se trouve sur le demi-axe positif Oz.

• son extrémité B décrit le demi-cercle de plan (xOy) de centre \(I(0,b,0)\) et de rayon \(b\), à la vitesse angulaire (par rapport à I) \(\omega\) constante et positive. A l’instant \(t=0\), B se trouve en O.

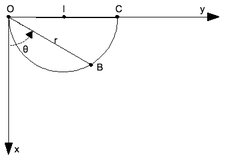
On note \(\phi\) l’angle \((\overrightarrow{IO}, \overrightarrow{IB})\).

1. Déterminer la durée T du mouvement

2. Déterminer une relation simple entre \(\phi\) et \(\theta\).

3. Etablir les expressions en fonction du temps \(t\) des coordonnées polaires \(r\) et \(\theta\) de B (cf. Figure).

4. Déterminer l’angle \(\alpha=(\overrightarrow{AO}, \overrightarrow{AB})\) en fonction de \(\omega\) et \(t\).

5. Calculer les coordonnées cylindriques \((R, \Theta)\) puis cartésiennes \(X,Y\) et \(Z\) du milieu J de la barre.

6. Déterminer la vitesse \(\overrightarrow{v_J}\) et l’accélération \(\overrightarrow{a_J}\) de J, ainsi que leur normes.

Point utile pour cet exercice

• \(\Longrightarrow\) Trigonométrie.

• \(\Longrightarrow\) Vitesse en cartésien.

Eléments de réponse (sans justification)

\(\theta(t) = \frac{\omega}{2}t\) et \(r(t) = b \sqrt{2 (1 - \cos \omega t)}\)et \(z(t) = 2b^2 (1 + \cos \omega t)\)

Rotation de la Terre

On assimile la Terre à une sphère de rayon \(R_T = 6400 \rm{km}\) et tournant sur son axe en 24h à vitesse angulaire constante \(\omega\). On considère un point M situé à une colatitude \(\theta\). L’axe (Oz) de référence étant l’axe de révolution de la Terre.

1. Déterminer \(\omega\).

2. Déterminer la position, la vitesse et l’accélération de M en fonction de \(\omega, R_T\) et t. On prendra soin de définir correctement le repère de projection.

Point utile pour cet exercice

• \(\Longrightarrow\) Base sphérique.

• \(\Longrightarrow\) Vitesse en spérique.

Eléments de réponse (sans justification)

\(\omega = 0.72 \times 10^{-4} rad.s^{-1}\)

Moment cinétique sur un axe.

On considère point matériel M de masse \(m\) en mouvement. On considère un axe \(\Delta\) orienté fixe dans un référentiel \(\mathfrak{R}\) et deux points A et B sur l’axe \(\Delta\).

Montrer que le moment cinétique de M sur l’axe \(\Delta\) dans \(\mathfrak{R}\) est le même qu’on le calcul avec le point A ou avec le point B.

Point utile pour cet exercice

• \(\Longrightarrow\) Moment cinétique.