4.1.2. Oscillateur harmonique

4.1.2.1. Oscillateur harmonique: Equation

Important

Equation différentielle d’un oscillateur harmonique

Un oscillateur harmonique est un système dont l’équation d’évolution s’écrit:

\[ \frac{\rm{d^2}x}{\rm{dt^2}}(t) + \omega_0^2 x(t) = \omega_{0}^2 x_{eq} \]

On rappelle qu’on peut annuler le second membre constant en procédant à un changement de variable \(X = x - x_{eq}\). Pour la suite, on étudiera directement l’équation sans second membre.

Important

Energie potentielle

La résultante des forces en mécanique s’écrit donc sous la forme \(\overrightarrow{F} = - k x \overrightarrow{e_x}\) et elle dérive d’une énergie potentielle sous la forme \(E_p = \frac{1}{2}k x^2\)

Attention: ces expressions seront à modifier suivant le système de coordonnées choisi.

4.1.2.2. Evolution temporelle

Exercice

1. Donner les deux formes générales de \(X(t)\)

2. Déterminer les constantes d’intégration sous les deux formes pour des conditions initialles à \(t=0\): \(x(t=0) = x_0; v(t=0) = v_0\).

3. Vérifier qu’il y a isochronisme des oscillations.

4. Représenter graphiquement l’évolution temporelle de \(X(t)\).

4.1.2.3. Evolution énergétique

Exercice

On suppose que les oscillations sont d’amplitude \(x_0\).

1. Exprimer l’énergie potentielle et l’énergie cinétique au cours du temps.

2. En déduire l’expression de l’énergie mécanique

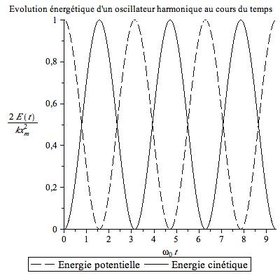
3. On a représenté graphiquement l’évolution temporelle des grandeurs énergétiques. Commenter les échanges d’énergie.