6.2.1. Méthodes

6.2.1.1. Cinétique

Calcul de la quantité de mouvement

1. On considère un cylindre d’axe Oz fixe dans un référentiel \(\mathfrak{R}\) et de masse uniformément répartie en rotation autour de l’axe Oz. Déterminer la quantité de mouvement du cylindre.

2. On considère un système composé de pièces de masse respectives \(m_1\) et \(m_2\). La première est en translation à une vitesse \(\overrightarrow{v_0}\) dans un référentiel \(\mathfrak{R}\). La seconde est en translation à une vitesse \(\overrightarrow{v_{2/1}}\) par rapport à la première pièce. Déterminer la quantité de mouvement du système total.

3. On considère un disque d’épaisseur \(h\) et de rayon \(R\) de masse totale \(M\) répartie de manière homogène. Il tourne autour d’un axe \(Oz\) où O est distance de \(R/2\) par rapport avec à G. La rotation se fait à vitesse angulaire constante \(\omega\). Déterminer la quantité de mouvement du disque.

Correction

1. Le cylindre étant de masse uniformément répartie, le centre d’inertie est situé sur l’axe de rotation et sa vitesse est nulle. Il vient:

(6.1)\[\begin{equation} \overrightarrow{p}_{cylindre} = M \overrightarrow{v}_{G/\mathfrak{R}} = \overrightarrow{0} \end{equation}\]

1. On décompose le système total en deux parties correspondant aux deux pièces:

(6.2)\[\begin{equation} \overrightarrow{p}_{total} = \overrightarrow{p}_{1} + \overrightarrow{p}_{2} = m_1 \overrightarrow{v_0} + m_2 \left ( \overrightarrow{v_2/1} + \overrightarrow{v_0}\right) \end{equation}\]

1. On pose un système de coordonnées cylindriques d’axe Oz.

On a indicé le vecteur \(\overrightarrow{e}_{\theta}\) pour bien préciser que la base locale est par rapport au point G. S’il n’y a pas d’ambiguité, cette précision n’est pas nécessaire.

(6.3)\[\begin{equation} \overrightarrow{p}_{cylindre} = M \overrightarrow{v}_{G/\mathfrak{R}} = M \frac{R}{2} \omega \overrightarrow{e}_{\theta,G} \end{equation}\]

Moment d’inertie et moment cinétique

1. On considère un solide S constitué de deux tiges de longueurs L pouvant coulisser l’une sur l’autre. La tige placée en dessous est accrochée par une extrémité à un axe fixe dans un référentiel \(\mathfrak{R}\). Préciser sans calcul pour quelles positions de la tige supérieure le moment d’inertie est maximal ou minimal.

2. Déterminer le moment d’inertie d’un point matériel de masse m sur un axe\(\Delta\) situé à une distance d.

3. On considère deux cylindriques concentriques de moment d’inertie respectifs \(J_1\) et \(J_2\) sur leur axe de symétrie et tournant chacun à des vitesses angulaires \(\omega_1\) et \(\omega_2\) autour de cet axe. Déterminer le moment cinétique et l’énergie cinétique de l’ensemble constitué des deux cylindres.

Correction

1. Il faut

   • que la répartition de masse soit la plus éloignée de l’axe pour que le moment soit maximale. La tige coulissante doit donc être au bout de la tige, côté extérieur (côté mobile)/

   • que la répartition de masse soit la plus proche de l’axe pour que le moment soit minimale. La tige coulissante doit donc être centrée sur l’axe de rotation.

2. \(md^2\)

3. Les cylindres ne tournant pas à la même vitesse, il faut _décomposer le système en deux sous-systèmes composés des deux cylindres. Il vient:

\[ L_{total} = J_1 \omega_1 + J_2 \omega_2 \]

6.2.1.2. Force et statique

Force et moment résultant

On considère une tige de longueur \(L\) dont le milieu est noté O qu’on prend comme origine d’un repère cartésien \((O, \overrightarrow{e}_x, \overrightarrow{e}_y, \overrightarrow{e}_z)\). Elle soumise à une action extérieure uniforme sur toute sa longueur. Cette action globale est décomposée en des actions quasi-ponctuelles : on suppose qu’un petit élément de longueur \(dl\) de la tige est soumis à une action quasi-ponctuelle \(\overrightarrow{dF} = \Lambda dl \overrightarrow{e}_x\) avec \(\overrightarrow{e}_x\).

1. Déterminer par intégration la force résultante \(\overrightarrow{F}\) exercée sur la tige.

2. Déterminer par intégration le moment résultant \(\overrightarrow{M}_A\) calculé au point A de l’action considérée, A étant une extrémité de la tige. On traitera deux cas :

   • La tige est suivant l’axe Ox (A est en \(x=-\frac{L}{2}\)).

   • La tige est suivant l’axe Oy (A est en \(y=-\frac{L}{2}\)).

3. Reprendre les mêmes calculs pour calcul le moment résultant au point O.

Le paramétrage de l’intégrale est à comprendre pour les chapitres à venir. Il est VIVEMENT conseillé de faire un schéma puor comprendre le paramètrage et le signe du moments.

Correction

1. Il suffit d’intégrer la force le long de la tige:

\[ \overrightarrow{F} = \int_{l=0}^{l=L} \Lambda dl \overrightarrow{e}_x = \Lambda L \overrightarrow{e}_x \]

2. De même :

\[ \overrightarrow{M}_A = \int_{M \in tige} \overrightarrow{AM} \wedge \Lambda dl \overrightarrow{e}_x \]

• Premier cas: \(\overrightarrow{AM} = (x + \frac{L}{2})\overrightarrow{e}_x\) et \(dl=dx\) soit :

\[ \overrightarrow{M}_A = \int_{x=\frac{-L}{2}}^{x=\frac{L}{2}} (x + \frac{L}{2})\overrightarrow{e}_x \wedge \Lambda dx \overrightarrow{e}_x = 0 \]

C’est logique car en chaque point, la force est colinéaire au vecteur \(\overrightarrow{AM}\) d’où un moment nul.

• Deuxième cas: \(\overrightarrow{AM} = (y + \frac{L}{2})\overrightarrow{e}_y\) et \(dl=dy\) soit :

\[ \overrightarrow{M}_A = \int_{y=\frac{-L}{2}}^{y=\frac{L}{2}} (y + \frac{L}{2})\overrightarrow{e}_y \wedge \Lambda dy \overrightarrow{e}_x = - \Lambda \frac{L^2}{2}\overrightarrow{e}_z \]

La force tend effectivement à faire tourner la tige autour de A dans le sens des \(-\overrightarrow{e}_z\), c’est cohérent. 3. Dans le deux cas, le moment est nul.

• Premier cas : même raisonnement que précédemment.

• Deuxième cas : On a \(\overrightarrow{OM} = y\) d’où une intégrale nulle. C’est logique car cette fois les effets de rotation autour de O sont compensés deux à deux par les actions locales.

Cet exercice montre comment calculé les composantes d’une actions de contact quand elles ne sont pas connues : en utilisant les théorèmes TMC et TRD.

Equilibre d’un cube

On étudie un cube (de masse uniformément répartie) sur un plan incliné. On admet qu’à l’équilibre, la somme des forces résultats est nulle et la somme des moments résultants en un même point est nulle.

1. Représenter la force résultante de l’action du poids en un point judicieusement choisi.

2. On considère un point B à la surface du plan situé au plus bas ou plus haut que le cube (donc pas sur la surface de contact). En raisonnant sur les actions ponctuelles de contact, justifier que le moment résultant en B ne peut jamais être nul.

3. Le cube est immobile. Par une analyse du bilan des actions, représenter la force résultante de l’action du plan incliné sur le cube en un point où son moment est nul.

4. Que se passe-t-il si l’on incline trop le plan ?

On pourrait remarquer que le moment résultant du poids est aussi nul en tout point à la verticale de G. Le choix de le représenter en G plutôt qu’en un autre point à sa verticale reste arbitraire.

Correction

1.Force résultante du poids. Le poids estune action globale qui n’a pas de point d’application. MAIS, on a vu qu’une action globale était mathématiquement équivalente à une action ponctuelle en un point de moment résultant nul. Un tel point est donc un bon endroit pour “représenter” une action globale.
Dans le cas du poids, on sait que le moment résultant est nul au centre d’inertie (champ de pesanteur uniforme) donc on va représenter le poids en G, le centre du cube.

2.Signe du moment
On rappelle que l’action de contact ponctuelle du plan sur le cube est forcément dirigée vers l’extérieur du plan incliné (non interpénétration) donc:

• Si B est plus bas que le cube, les moments de TOUTES les actions ponctuelles en B sont non nuls et dirigés dans le même sens : leur somme sera donc non nulle

• Le raisonnement est le même si B est au dessus du cube.

3.Force résultante de la réaction. Deux forces s’appliquent sur le cube : son poids et l’action du support. La somme des forces est nulle à l’équilibre, donc la force résultante de l’action du support est un vecteur force opposé : \(\overrightarrow{R} = - \overrightarrow{P}\).
On va de même chercher un point de moment résultant nul. A l’équilibre, la somme des moments résultants en un même point est nul (TMC). Donc si le moment du poids en un point B est nul, le moment de l’action du support est aussi nul en B. Il vient que le moment de l’action du support est nul en tout point à la verticale de G (car \(\overrightarrow{R}\) est verticale).
Pour garder le sens physique de l’action de contact, on aura tendance à représenter \(\overrightarrow{R}\) au point d’intersection entre cette verticale et le plan incliné.

4.Inclinaison du plan
Si l’on incline trop le cube, on observe que l’intersection (notée B) entre la verticale en G etle plan incliné se retrouve hors du cube (angle supérieur à 45 degré). Hors, nous avons vu que le moment ne pouvait être nul en un tel point : le cube ne peut être en équilibre aux fortes pentes, il va basculer.

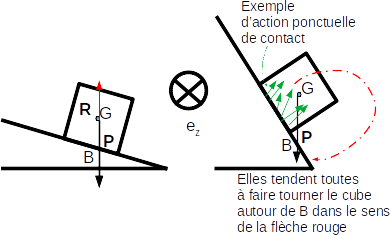
Fig. 6.1 Actions sur le cube

Cylindre sur plan incliné

On considère un cylindre de rayon R, de hauteur h et de masse M uniformément répartie placé sur un plan incliné d’angle \(\alpha\).

1. Sur un plan de coupe, représenter les forces résultantes associées à chaque action extérieure sur le cylindre. On distinguera deux cas suivant le comportement de l’action de contact.

2. Le cylindre peut-il rester immobile ? Peut-il glisser sans rouler ? Peut-il rouler sans glisser ? On expliquera ceci au moyen d’un bilan des actions.

Correction

Le raisonnement sur le cube peut-être refait ici et montre que le même résultant de l’action du plan sur le cylindre ne peut-être nul que sur l’arête de contact entre le cylindre et le plan incliné. Le poids est lui toujours de moment nul en G. On observe, une fois le schéma réalisé (s’entraîner à le faire), que la somme des moments est nécessairement non nulle donc le cylindre ne peut rester immobile et va forcément tourner (rouler). Il n’y a par contre pas a priori de contradiction à un roulement sans glissement.

6.2.1.3. Dynamique

Volant freiné

On considère un volant qui tourne autour d’un axe fixe horizontal. Son moment d’inertie autour de cet axe vaut J. Son centre d’inertie est sur l’axe et le champ de pesanteur est uniforme et constant. Au cours du mouvement, le volant subit des frottements solides qu’on modélise comme un couple constant dont le moment par rapport à l’axe de rotation est \(\vert M_f \vert = \alpha J\) avec \(\alpha\) constant. On lance le volant à une vitesse angulaire \(\omega_0\) et celui-ci s’immobilise après N tours.

1. Exprimer le coefficient \(\alpha\) en fonction de \(\omega_0\) et N.

Correction

On va appliquer un TMC sur l’axe de rotation appliqué au système {volant} dans le référentiel terrestre supposé galiléen. Les forces qui s’appliquent sur le système sont:

• son poids : le moment sur l’axe est nul puisque que le centre d’inertie (point de moment nul du poids) est sur l’axe.

• l’action de l’axe sur le volant : son moment est celui des frottements solides \(M_f = - J \alpha\) si l’on suppose \(\omega > 0\) la vitesse angulaire.

Le TMC s’écrit donc:

\[\begin{align*} J \frac{\rm{d}\omega}{\rm{dt}} &= -J \alpha\\ \omega &= -\alpha t + \omega_0 \\ \theta &= -\frac{\alpha}{2} t^2 + \omega_0 t \end{align*}\]

Le volant s’arrête donc pour \(t_f = \frac{\omega_0}{\alpha}\), il a alors tourner de :

\[ \theta_f = \frac{\omega_0^2}{2\alpha} = 2 \pi N \]

Il vient:

\[ \alpha = \frac{\omega_0^2}{4 \pi N} \]

Cet exercice présente trois points importants: la capacité à paramétrer correctement un problème, le calcul d’un moment d’une force et l’analyse physique d’un système en rotation par étude des moments. Nous en profiterons pour aborder qualitativement deux notions importantes: la notion d’équilibre et la notion de stabilité.

Cas d’un système de points.

On considère un cube de côté a et de répartition de masse uniformément répartie en liaison pivot avec un axe passant par le centre du cube et perpendiculaire à deux des faces du cube. Le cube ne peut ainsi que tourner autour de cet axe supposé fixe dans un référentiel \(\mathfrak{R}\). Tous les éléments cinématiques et cinétiques devront être établis dans ce référentiel qu’on supposera galiléen.

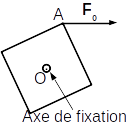
On attache un fil tendu à un coin du cube noté A. On considère que la liaison entre le cube et le fil se résume à un seul point de sorte qu’on puisse considérer l’action du ressort sur le cube comme ponctuelle. La force appliqué par le fil sur le cube est toujours horizontale et de norme \(F_0\).

1. Paramétrer le problème (proposer un système de coordonnées et des paramètres utiles au problème) pour pouvoir étudier la rotation du cube autour de son axe. Proposer alors une expression du moment cinétique du cube sur l’axe de rotation,de son énergie cinétique et de sa quantité de mouvement. On notera J le moment d’inertie du cube sur l’axe de rotation et M sa masse totale.

2. Exprimer le moment de la force exercé par le fil sur le cube exprimé au centre du cube. Commenter suivant les valeurs des paramètres introduits la tendance qu’aura cette force à agir sur la rotation du cube.

3. On suppose la liaison pivot parfaite. Quelles sont les positions d’équilibre du système ? Si l’on écarte légèrement le cube de chacune de ces positions, aura-t-il tendance a revenir à la position d’équilibre ? (On parle de stabilité des positions d’équilibre).

Correction

1. Paramétrage

Pour étudier un système en rotation autour d’un axe fixe, le système de coordonnées le plus judicieux est un système de coordonnées cylindrique d’axe Oz l’axe de rotation. On a représenté ci dessous le système. On repère l’angle \(\theta\) permettant de repérer l’orientation du cube par l’angle \((\overrightarrow{e_x},\overrightarrow{OA})\) de manière à pouvoir utiliser cet angle pour les calculs de moments.

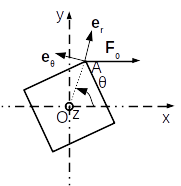
On peut alors écrire les éléments cinétiques du cube:

\[\begin{align*} L_{Oz}(cube) &= J \dot \theta \\ E_{c,cube} &= \frac{1}{2} J \dot \theta^2\\ \overrightarrow{P_{cube/\mathfrak{R}}} = M \overrightarrow{v_{G}} = \overrightarrow{0} \end{align*}\]

Le cube étant de masse répartie de manière homogène, le centre d’inertie est situé au point O, centre du cube. Fixé sur l’axe Oz, le centre d’inertie est donc immobile, d’où la quantité de mouvement nulle.

Les deux autres expressions sont les expressions déjà données dans le cas d’un solide en rotation autour d’un axe fixe.

2. Calcul de moment de l’action/la force

L’action du fil sur le cube est une action ponctuelle dont la force s’écrit \(\overrightarrow{F} = F_0 \overrightarrow{e_x}\) et dont le point d’application est A. Le moment de l’action du fil sur le cube calculé sur l’axe Oz s’écrit (O est un point de l’axe… Oz):

\[\begin{align*} M_{fil \to cube,Oz} &= \overrightarrow{e_z} \cdot \left(\overrightarrow{OA} \wedge \overrightarrow{F}\right)\\ &= \overrightarrow{e_z} \cdot \left(\left(\frac{a}{\sqrt{2}} \overrightarrow{e_r} + \frac{a}{2} \overrightarrow{e_z}\right) \wedge F_0 \overrightarrow{e_x}\right)\\ &= \overrightarrow{e_z} \cdot \left(\frac{aF_0}{2} \overrightarrow{e_y} - \frac{a}{\sqrt{2}} F_0 \sin \theta \overrightarrow{e_z} \right)\\ &= - \frac{a}{\sqrt{2}} F_0 \sin \theta \\ \end{align*}\]

3. Positions d’équilibre et stabilité On remarque que si \(\theta\) est positif, le moment de l’action est négatif: l’action du fil aura tendance à faire tourner le cube dans le sens des \(\theta\) décroissants. A l’inverse, si \(\theta\) est négatif, le moment de l’action est positif: l’action du fil aura tendance à faire tourner le cube dans le sens des \(\theta\) croissants. C’est cohérent avec le schéma représenté ci-dessous.

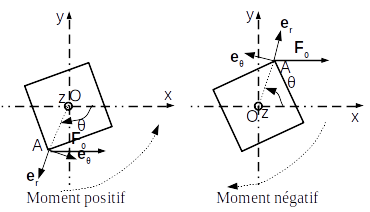
On va appliquer un TMC sur l’axe de rotation au cube. Le poids est de moment nul (centre d’inertie sur l’axe) et la liaison pivot aussi (liaison parvaite). Le TMC devient donc:

\[\begin{split} J_{cube} \frac{\rm{d^2}\\theta}{\rm{dt^2}} = - \frac{a}{\sqrt{2}} F_0 \sin \theta \end{split}\]

Donc, les angles pour lesquels le moment de l’action du fil est nul seront les positions d’équilibre. L’expression précédente montre que les deux positions correspondent aux angles \(\theta = 0\) et \(\theta = \pi\). On a représenté les positions d’équilibre ci-dessous.

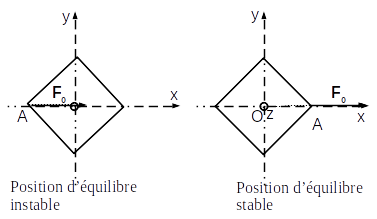
On remarque que si l’on écarte légèrement le cube de sa position d’équilibre \(\theta = 0\) vers des angles positifs, l’angle va décroitre sous l’effet de l’action du fil (cf. schéma du signe du moment) et il va donc avoir tendance à revenir vers la position d’équilibre. A l’inverse, si \(\theta\) est négatif, l’angle va croitre (schéma du signe du moment) et va aussi revenir vers la position d’équilibre. Donc lorsqu’on écarte le système de cette position d’équilibre, il tend à y revenir, on dit que la position d’équilibre est stable.

On pourrait montrer que l’action du fil dérive d’une énergie potentiel et faire une étude énergétique des équilibres.

A l’inverse si l’on écarte le cube de sa position d’équilibre \(\theta = \pi\), on remarque qu’il va s’éloigner de cette position. En effet, pour \(\theta < \pi\), le moment est négatif et l’angle va encore décroître. Et pour \(\theta > + pi\), le moment est positif et l’angle va croître. Dans les deux cas, on s’éloigne de la position d’équilibre: la position est dite instable.