Généralités

Dans tout le chapitre, le système sera un point matériel noté M.

Intérêt

Les intégrales premières du mouvement sont extrêmement importantes car elles permettent d’établir des équations d’ordre 1. On peut alors utiliser comme conditions initiales, non pas les données de positions et de vitesses mais les valeurs de ces intégrales premières du mouvement.

Rappel : Intégrale première du mouvement

Une intégrale première du mouvement est une grandeur dépendant de la position et de sa dérivée temporelle et qui est constante au cours du mouvement.

On a vu que pour un système conservatif, l’énergie mécanique, qui ne dépend que de la vitesse (par l’énergie cinétique) et de la position (par l’énergie potentielle) est une intégrale première du mouvement.

Définition

Le référentiel sera toujours supposé galiléen.

Important

Mouvement à force centrale

Un mouvement à force centrale est un mouvement dont la résultante des forces est toujours dirigée vers un même point O fixe dans le référentiel considéré.
On appelle le point O le centre de force car en effet le point O est responsable de la force.

Conservation du moment cinétique

Important

Conservation du moment cinétique

Dans un mouvement à force centrale dont le centre de force est le point O, alors le moment cinétique au point O est une intégrale première du mouvement.

Cela signifie qu’il est constant au cours du mouvement.

Démonstration

On va appliquer au système M le théorème du moment cinétique au point O. La résultante des forces étant portée par la droite OM, son moment en O est nul. Il vient que la dérivée du moment cinétique est nulle: le moment cinétique est donc une constante du mouvement.

Par définition, le moment cinétique dépend de la position et de la vitesse. C’est donc une intégrale première du mouvement.

Important

Conséquence : Planéité du mouvement

Un mouvement à force centrale est un mouvement plan: la trajectoire du mobile est contenu dans le plan passante par le centre de force O et perpendiculaire au moment cinétique.

Démonstration

Nous avons démontré que le moment cinétique était un vecteur constant. Or par définition du moment cinétique, le vecteur position pris au point O est perpendiculaire au moment cinétique. Il vient que le vecteur position est à tout instant perpendiculaire au même vecteur: il est contenu dans le plan passant par O et perpendiculaire au moment cinétique.

Important

Paramétrage

La planéité du mouvement et le caractère centrale de la force explique le choix du paramétrage. Par la suite, on va travailler dans un repère cylindrique centré au point O et d’axe Oz suivant le moment cinétique. On notera le moment cinétique au point O: \(\overrightarrow{L_O} = L_O \overrightarrow{e_z}\).

On peut alors exprimer le moment cinétique dans le système de coordonnées:

\[\begin{align*} \overrightarrow{L_O} &= \overrightarrow{OM} \wedge m \overrightarrow{v_{M}}\\ &= r \overrightarrow{e_r} \wedge m \left(\dot r \overrightarrow{e_r} + r \dot \theta \overrightarrow{e_{\theta}}\right)\\ &= m r^2 \dot \theta \overrightarrow{e_z} \end{align*}\]

On remarquera que le moment cinétique est une donnée constante qui peut être utilisée comme “donnée initiale” comme on le verra par la suite. Son expression montre que l’on relie l’évolution angulaire au rayon. Il vient qu’on par d’un système à 2 degré de liberté (rotation autour de O donné par \(\dot \theta\) et éloignement/rapprochement de O donné par \(r\)) et qu’on lie l’évolution des mouvements. On pourra donc, en introduisant le moment cinétique \(L_O\) éliminer la vitesse angulaire dans les équations.

Important

Conséquence : Loi des aires

Dans un mouvement à force centrale, la vitesse aréolaire, c’est-à-dire l’aire parcourue par le vecteur position par unité de temps est constante.

Démonstration

Durant un temps dt, le mobile passe du point \(M(t)\) au point \(M(t+dt)\). L’aire balayée est donc l’aire du triangle \(OM(t)M(t+dt)\). L’aire de ce triangle s’écrit:

\[\begin{align*} d\mathfrak{A} &= \frac{1}{2} \left\vert \overrightarrow{OM}\wedge\overrightarrow{M(t)M(t+dt)} \right\vert \\ &= \frac{1}{2m} \left\vert \overrightarrow{OM}\wedge m\overrightarrow{v_M}dt \right\vert \\ &= \frac{1}{2m}\left\vert \overrightarrow{L_O} \right\vert dt \\ \frac{\rm{d}\mathfrak{A}}{\rm{dt}} &= \frac{1}{2m} L_O \end{align*}\]

Le moment cinétique étant constant, il vient que la vitesse aréolaire est constante. La loi des aires est bien vérifiée.

Important

Constante des aires

On définit la constante des aires comme la grandeur \(C = r^2 \dot\theta\). Dans un mouvement à force centrale, il s’agit évidemment d’une constante et la vitesse aréolaire s’écrit \(\frac{\rm{d}\mathfrak{A}}{\rm{dt}} = \frac{1}{2}C\).

Cas conservatifs

Généralités

Important

Force centrale conservatives

Une force centrale conservative ne dépend que de la coordonnées radiale. On peut donc écrire \(\overrightarrow{F} = F(r) \overrightarrow{e_r}\) et l’énergie potentielle associée \(E_p(r)\) est telle que \(F(r) = - \frac{\rm{d}E_p}{\rm{dr}}(r)\).

Démonstration

Démonstration La force est uniquement suivant \(\overrightarrow{e_r}\) par définition d’une force centrale. Il vient (gradient) que les dérivées partielles de l’énergie potentielle par rapport à \(\theta\) et z sont nulles: l’énergie potentielle ne dépend que de r. En dérivant, il vient que la force ne dépend aussi que de r.

Conservation de l’énergie mécanique La seule force est conservative, donc l’énergie mécanique est une constante: c’est une intégrale première du mouvement. Comme nous l’avons expliqué, nous n’utiliserons que très rarement des données initiales sur la vitesse et la position. Elles seront remplacées par les données de l’énergie mécanique et du moment cinétique qui sont des constantes du mouvement.

A un instant t quelconque, l’énergie mécanique s’écrit:

(10)\[\begin{equation} E_m = \frac{1}{2}m \dot r^2 + \frac{1}{2}m r^2 \dot \theta^2 + E_p(r) \end{equation}\]

Interprétation de l’énergie cinétique.

L’énergie cinétique se réécrit:

\[ E_c = \frac{1}{2}m \dot r^2 + \frac{1}{2}m r^2 \dot \theta^2 \]

On distingue donc deux termes:

• Le premier correspond à l’éloignement/rapprochement du mobile. On l’appelera énergie cinétique radiale.

• Le second correspond à la rotation du mobile autour de O, on l’appelera énergie cinétique orthoradiale (ou de rotation).

Energie potentielle effective

But

Le but est d’éliminer la vitesse angulaire pour n’avoir une énergie mécanique s’exprimant uniquement en fonction du rayon et de sa dérivée temporelle. On introduira alors l’énergie mécanique sous la forme:

\[\begin{align*} E_m &= E_{c,r} + E_{p,eff}(r)\\ &= \frac{1}{2}m \dot r^{2} + E_{p,eff}(r) \end{align*}\]

L’intérêt de pouvoir utiliser la positivité de l’énergie cinétique radiale pour obtenir des informations. Comme nous allons le voir, nous obtiendrons plus d’informations qu’avec la seule positivité de l’énergie cinétique complète.

Important

Expression de l’énergie potentielle effective.

Dans le cadre d’un mouvement à force centrale, on peut réécrire l’énergie mécanique sous la forme:

\[\begin{align*} E_m &= E_{c,r} + E_{p,eff}(r)\\ &= \frac{1}{2}m \dot r^{2} + E_{p,eff}(r) \end{align*}\]

où l’énergie potentielle effective a pour expression:

\[\begin{align*} E_{p,eff}(r) &= E_{c,\theta} + E_{p}(r)\\ &= \frac{1}{2}m r^{2}\dot \theta^{2} + E_{p}(r)\\ &= \frac{L_0^{2}}{2m r^{2}} + E_p(r)\\ &= \frac{mC^{2}}{2r^{2}} + E_p(r) \end{align*}\]

où \(C\) est la constante des aires et \(L_O\) est la composante du moment cinétique.

Barrière de potentiel en r=0

Le terme ajouté \(\frac{1mC^2}{2r^2}\) tend vers \(+ \infty\) en \(r=0\). Cela signifie que ce terme énergétique tend à empêcher le mobile d’atteindre le centre de force en lui opposant une barrière d’énergie infinie.

A partir du moment où le mobile tourne, il faudra une énergie potentielle tendant très rapidement vers \(- \infty\), c’est-à-dire que la force doit être très attractive, pour que cette barrière infinie soit compensée et que le centre de force soit accessible. Dans de nombreux cas usuels, la barrière infinie n’est pas compensée.

Interprétation

Nous allons détailler les caractéristiques qu’on peut déduire de l’énergie potentielle effective mais comme nous l’avons dit, on peut déjà remarquer que \(\frac{1}{2}m \dot r^{2}\) est positif ou nul. Cela implique que l’énergie potentielle effective est nécessairement inférieure à l’énergie mécanique.

Comme pour le cas des mouvements conservatifs, cela va interdire certaines zones. Mais cette condition est plus contraignante car l’énergie potentielle effective est plus grande que l’énergie potentielle (le terme d’énergie cinétique orthoradiale est positive - strictement si le moment cinétique est non nul).

Analyse semi-qualitatives

Positivité de l’énergie cinétique

On rappelle que l’énergie cinétique radiale est nécessairement positive ou nulle. Cela permet de déterminer des zones accessibles. Nous allons préciser ici ce principe en remarquant que les zones accessibles sont un peu particulières. Ici le système est à deux degrés de liberté: sa position radiale et sa position angulaire.

Important

Zones accessibles

Les zones où \(E_{p,eff}(r) > E_m\) sont inaccessibles. Cela correspond à des rayons inaccessibles soit à des zones limitées par des cercles.. Les zones accessibles et inaccessibles sont dont définies comme des zones comprises entre des cercles de centre O où \(E_ {p,eff}(r) = E_m\).

• Si la trajectoire est limitée par un rayon maximal, l’état sera lié.

• Si la trajectoire n’est pas limitée par un rayon maximal, l’état sera de diffusion.

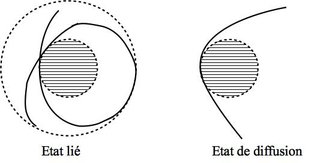
Les rayons extrêmes atteints seront données par l’équation \(E_{p,eff} = E_m\). De même, le mobile ne peut change la variation de r (passer d’éloignement à rapprochement ou inversement) qu’aux position extrêmes car ce sont les positions où la vitesse radiale s’annule. La trajectoire est y est tangente au cercle.

Positions extrêmes et vitesse

ATTENTION ! Aux rayons extrêmes, seule la vitesse radiale s’annule. La vitesse totale n’est pas nulle. En effet, si le moment cinétique n’est pas nulle, il vient que la vitesse orthoradiale ne s’annule jamais.

Nous verrons même des exemples où la vitesse sera maximale pour l’un des deux rayons extrêmes.

Caractéristiques autres

Important

Minimum d’énergie potentielle effective

• Le minimum d’énergie potentielle effective ne correspond pas à une position d’équilibre possible du système. On rappelle que le moment cinétique est non nul, donc il y a toujours le mouvement de rotation.

• Au minimum d’énergie potentielle effective, la vitesse n’est pas non plus maximale (cf. remarque précédente). Seule la vitesse radiale y est maximale.

• Par contre, si l’énergie mécanique égale la valeur minimale de l’énergie potentielle effective, alors un seul rayon est accessible: la trajectoire sera donc un cercle.

TrajectoireS circulaireS

Bien qu’il n’apparaissent souvent qu’un seul minimum sur les tracés d’énergie potentielle effective, il existe en réalité une infinité de trajectoires circulaires possibles suivant la valeur du moment cinétique. Une variation de ce dernier fait varier le tracé même de \(E_{p,eff}(r)\) et donc la position du minimum.

On déduit en général, non pas une valeur de R, mais une relation entre le rayon du cercle et la vitesse du mobile.