4.2. Etude des pendules#
Compétences
Etablir l’équation du mouvement du pendule simple
Etablir l’équation du mouvement du pendule pesant.
Justifier l’analogie avec l’oscillateur harmonique dans le cadre de l’approximation linéaire (pendule simple ou pesant)
Etablir l’équation du portrait de phase dans le cadre des faibles oscillations et le tracer.
Lire et interpréter le portrait de phase: bifurcation entre un mouvement pendulaire et un mouvement révolutif.
Mettre en évidence le non isochronisme des oscillations
Etablir l’équation du mouvement d’un pendule de torsion
Expliquer l’analogie entre le pendule de torsion et l’oscillateur harmonique
Etablir une intégrale première du mouvement.
4.2.1. Pendule simple#
Un pendule simple est constitué d’un fil parfait (ou d’une tige parfaite) de longueur L au bout duquel on attache une masse m assimilable à un point matériel (noté M). Dans cet exercice, on considère le cas d’une tige rigide.
Ici, l’autre extrémité de la tige est attachée à un point O fixe dans le référentiel terrestre supposé galiléen.
Le champ de pesanteur est supposé uniforme.
PFD
Proposer un paramétrage adapté au problème.
Etablir l’équation qui régit l’évolution du pendule au moyen du principe fondamental de la dynamique.
TMC
En utilisant le même paramétrage que dans l’exercice précédent, établir à nouveau l’équation d’évolution du pendule mais en utilisant le théorème du moment cinétique.
TEM
En utilisant le même paramétrage que dans l’exercice précédent, établir à nouveau l’équation d’évolution du pendule mais en utilisant le théorème de la puissance mécanique.
Reconnaître une intégrale première du mouvement, c’est-à-dire une grandeur ne dépendant que de la position et de sa dérivée première et qui est constante au cours du mouvement.
4.2.2. Petits mouvements#
Exercice
On considère le pendule simple.
Linéariser l’équation d’évolution pour des petits mouvements autour de la position d’équilibre stable. Comment appelle-t-on un tel système ?
Préciser la forme temporelle de l’évolution du système ainsi que la période des oscillations.
La période des oscillations dépend-t-elle des conditions initiales (dans l’hypothèse des petites mouvements). On parle d’isochronisme des oscillations.
4.2.3. Etude générale#
On considère à nouveau le pendule simple mais on ne suppose plus qu’on est aux petits angles.
Etude énergétique
En étudiant l’énergie potentielle du pendule simple, montrer:
l’existence de deux types de mouvements suivant l’énergie mécanique: un mouvement pendulaire et un mouvement circulaire complet.
L’existence de deux positions d’équilibre: l’une stable et l’autre instable.
Si le mobile part du point le plus bas avec une vitesse linéaire \(v_0\). Déterminer l’angle \(\theta_{\max}\) le plus haut qu’il peut atteindre en fonction de \(v_0\) ainsi que la valeur minimale de \(v_0\) permettant en pendule de faire des tours complet.
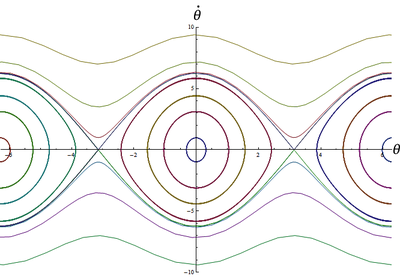
Reconnaître sur le graphique ci-après les différents cas: petits mouvements, grands mouvements pendulaire, tours complets.
Anisochronisme
On considère que le pendule est lâché d’un angle \(\theta_0 > 0\) avec la verticale descendante sans vitesse initiale.
Quelle est la nature du mouvement: pendulaire ou tour complet ?
A l’aide du théorème de l’énergie mécanique, exprimer la vitesse angulaire à un instant t où le pendule fait un angle \(\theta\) avec la verticale descendante.
Déduire de l’équation précédente que la période d’oscillation T est: \(T = 4 \int_0^{\theta_0} \frac{d \theta}{\sqrt{\frac{2g}{l} (cos \theta - cos \theta_0)}}\)
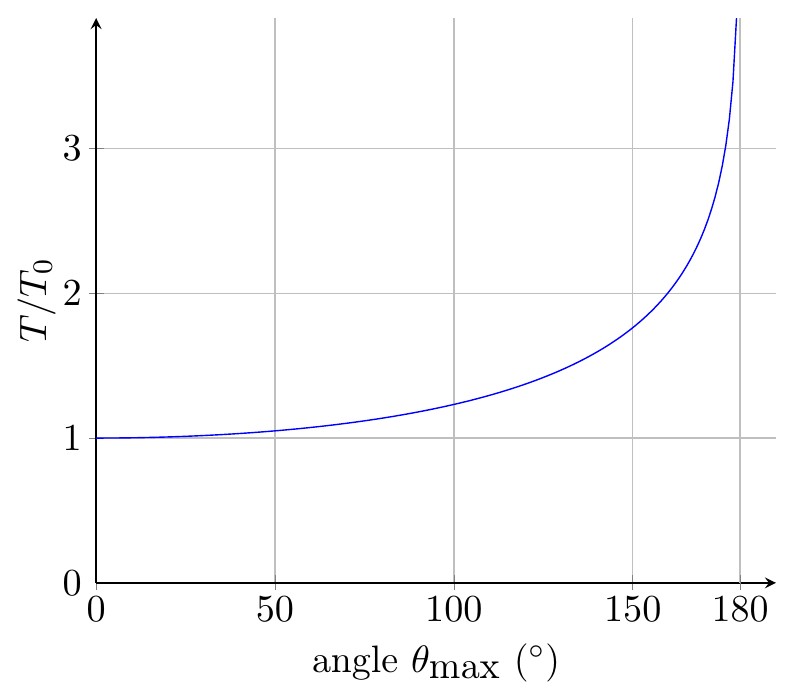
La période des oscillations est-elle indépendante de l’amplitude des oscillations? On parle d’anisochronisme des oscillations.
On a représenté ci-après le rapport \(T/T_0\) en fonction de l’angle \(\theta_0\) (noté \(\theta_{\max}\)). Commenter cette courbe.