5.2.5. Entrainement#
5.2.5.1. Forces centrales quelconques#
Point matériel lié à un fil
Un point matériel M de masse m se déplace sans frottement sur un plan horizontal. Il est attaché à un fil de masse négligeable. Le plan est percé au point O choisi pour origine, le fil traverse le plan en O; un opérateur exerce sur l’autre extrémité du fil une force de traction de module F constant.
A t=0, le point M se trouve sur l’axe Ox à une distance D de O, sa vitesse est alors \(V_0\), colinéaire à Oy.
Montrer que le moment cinétique \(\overrightarrow{L_O}\) en O de M se conserve pendant toute la durée de la traction. Calculer son module et sa direction. Définir la vitesse aréolaire et montrer que le mouvement de M se fait suivant la loi des aires, à savoir que la vitesse aréolaire est constante.
Déterminer l’énergie mécanique \(E_m\) de M; on montrera que la force de traction dérive d’une énergie potentielle \(E_p\) que l’on exprimera en utilisant les coordonnées cylindriques. On prendra \(E_p=0\) pour \(OM=0\).
Montrer que l’on peut écrire \(E_m\) comme une fonction de \(r\) seule et de ses dérivées et définir une fonction énergie potentielle effective.
Etudier ses variations en fonction de r=OM. Montrer qu’elle passe par un minimum pour \(r_1 = \left(\frac{m V_0^2 D^2}{F}\right)^{1/3}\).
Tracer le graphe correspondant et faire apparaître l’énergie mécanique. Déterminer graphiquement les deux distances extrêmes de M à O; à quelle condition sur F la position initiale est-elle le point de la trajectoire le plus éloigné de O? Le point matériel peut-il arriver jusqu’à O?
Quelle valeur donner à F pour observer un mouvement circulaire? Montrer qu’il est alors nécessaire uniforme.
Point utile pour cet exercice
\(\Longrightarrow\) Mouvement à force centrale.
\(\Longrightarrow\) Système conservatif.
\(\Longrightarrow\) Energie potentielle effective.
Mouvement d’une bille dans un cône
On considère un matériel M glissant sans frottements à l’intérieur d’un cône dont la génératrice fait un angle \(\alpha\) avec l’axe Oz vertical dirigé vers le haut, O étant le sommet du cône. On suppose le champ de pesanteur uniforme \(\overrightarrow{g} = - g \overrightarrow{e_z}\). On se place en coordonnées cylindriques d’axe Oz et de centre O. On travaille dans le référentiel terrestre qu’on supposera galiléen.
Déterminer la relation entre les coordonnées r et z. En déduire l’expression de la vitesse \(\overrightarrow{v}\) et de l’accélération \(\overrightarrow{a}\) en fonction de r et \(\theta\).
En déduire, en utilisant le principe fondamental de la dynamique que:
avec \(M = m (1+ \frac{1}{\tan^2 \alpha})\)
Exprimer le moment cinétique \(\overrightarrow{J_O}\) par rapport au point O en fonction de \(m, r, z\) et \(\theta\). Montrer que la composante suivant Oz, notée \(J_z\) est conservée au cours du mouvement.
En exprimant \(\dot \theta\) en fonction de \(J_z\), montrer que l’équation différentielle sur r peut s’écrire sous la forme: \(M \ddot r = - \frac{dV_{eff}(r)}{dr}\) où \(V_{eff}(r)\) est un potentiel effectif que l’on exprimera en fonction de \(\alpha\), m,g, et \(J_z\). Tracer les allures de \(V_{eff}(r)\) pour \(J_z = 0\) et pour \(J_z \neq 0\).
ATTENTION: Nous allons à partir de ce point réaliser une étude à partir du potentiel effectif comme elle a été faite en cours pour le cas des mouvements à force centrale. On remarquera néanmoins que le mouvement n’est PAS ici un mouvement à force centrale. On pourra s’en convaincre en remarquant par exemple que la composante du moment cinétique projeté sur \(\overrightarrow{e_{\theta}}\) n’est pas conservée (TMC) ou simplement parce que le mouvement n’est pas plan. La méthode d’analyse mathématique ne reste pas moins utilisable A CONDITION DE PROUVER QU’ON PEUT L’UTILISER.
Calculer l’énergie mécanique et montrer qu’elle peut s’écrire sous la forme: \(E_m = \frac{1}{2} M \dot r^2 + V_{eff}(r)\). Justifier le fait que l’énergie mécanique est conservée. On vérifiera que cette conservation permet bien de retrouver l’équation différentielle établie à la question précédente.
On s’intéresse uniquement aux trajectoires dont les conditions initiales sont de la forme \(r(0) = r_0, \overrightarrow{v}(0) = v_0 \overrightarrow{e_{\theta}}\).
Exprimer \(J_z\) en fonction de ces conditions initiales.
A quelle condition sur \(v_0\) la bille atteint-elle le fond du cône? Quelle est alors la trajectoire.
Déterminer \(v_0\) pour que la trajectoire soit un cercle de rayon \(r_0\) et d’altitude constante.
Montrer graphiquement que dans le cas général et si \(J_z \neq 0\) le mouvement est dans un état lié dont les rayons extrêmes sont \(r_{\min}\) et \(r_{\max}\) qu’on repérera graphiquement.
Point utile pour cet exercice
\(\Longrightarrow\) Mouvement à force centrale. (ou pas)
\(\Longrightarrow\) Système conservatif.
\(\Longrightarrow\) Energie potentielle effective.
5.2.5.2. Potentiels newtoniens#
Vecteur excentricité
On veut étudier le mouvement d’une planète P, assimilée à un point matériel dans le champ de gravitation d’une étoile de masse \(M_e\), de centre O considérée comme ponctuelle et fixe. La planète de masse \(M_P\) est située à une distance \(r=OP\) de O. On considère le référentiel lié à l’étoile comme galiléen.
Exprimer la force exercée par l’étoile sur la planète en fonction de \(M_p, M_e, r, G\) la constante de gravitation universelle et \(\overrightarrow{u_r} = \frac{\overrightarrow{OP}}{r}\).
Justifier que le mouvement est plan. Préciser ce plan.
On rappelle que l’équation polaire d’une ellipse est \(r(\theta) = \frac{p}{1+ e \cos \theta}\). On définit le vecteur excentricité: \(\overrightarrow{e} = - \frac{L}{GM_e M_P} \overrightarrow{v} + \overrightarrow{u_{\theta}}\) où \(\overrightarrow{v}\) est la vitesse de la planète.
Montrer que le vecteur excentricité est un vecteur constant. En fait, ce vecteur est orthogonal au grand axe de l’ellipse.
En calculant le produit scalaire \(\overrightarrow{e} \cdot \overrightarrow{u_{\theta}}\), montrer que l’on retrouve bien l’équation d’une ellipse.
Que vaut le module de \(\overrightarrow{e}\)? Préciser p en fonction de G, \(M_p\), \(M_e\) et L.
Préciser la valeur de l’excentricité dans le cas d’un mouvement circulaire.
Dans le cas d’un mouvement circulaire, préciser la valeur de L en fonction de R (rayon du cercle), \(v_c\) (vitesse circulaire) et \(M_p\). Déterminer l’expression de la vitesse \(V_c\) en fonction de R, G et \(M_e\) à l’aide du vecteur excentricité.
Point utile pour cet exercice
\(\Longrightarrow\) Mouvement des planètes.
\(\Longrightarrow\) Trajectoire elliptique.
\(\Longrightarrow\) Excentricité.
Explosion d’une comète
Une comète de période T=770 ans s’est approchée du soleil à \(d = 7,75 \times 10^{-3} \rm{u.a.}\)
On suppose que la trajectoire est elliptique. Déterminer le demi-grand axe a, l’excentricité e, le paramètre p de l’ellipse et les vitesses à l’aphélie (\(v_A\)) et au périhélie (\(v_P\)). A-t-on eu raison de faire l’hypothèse d’une trajectoire elliptique?
A son périhélie, elle a explosé en deux morceaux de masse \(m_1\) et \(m_2\), partis respectivement avec la vitesse \(v_1\) et \(v_2\) dans deux directions faisant des angles respectifs \(\alpha_1 = -20 ^{\circ}\) et \(\alpha_2 = 50 ^{\circ}\) avec la direction initiale de \(v_P\). La quantité de mouvement totale se conserve durant l’explosion et l’on observe que: \(\left \| v_1\right \| \sim \left \| v_2 \right \|\).
En utilisant la conservation de la quantité de mouvement, déterminer le rapport des masses \(m_1/m_2\) puis la norme des vitesses des fragments.
Calculer l’énergie mécanique par unité de masse pour chaque fragment. En déduire le type de la nouvelle trajectoire.
Point utile pour cet exercice
\(\Longrightarrow\) Lois de Kepler.
\(\Longrightarrow\) Trajectoire elliptique.
\(\Longrightarrow\) Energie mécanique.
Mise en orbite d’une sonde spatiale
On souhaite mettre en orbite une sonde spatiale(s) autour de Mars. Ce véhicule possède au point A la vitesse \(v_A\) et présente un “paramètre d’impact” b (cf. Figure). On donne:
\(v_A = 2,5 \rm{km/s}\)
rayon de Mars: \(r_M = 3397 \rm{km}\)
masse de Mars: \(M_M = 6,39 \times 10^{23} \rm{kg}\)
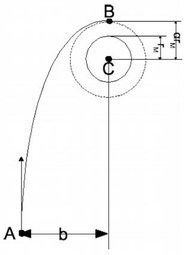
Remarque: Le point B n’est pas placé correctement sur le schéma. Cela n’a pas d’influence sur les raisonnements.
Au point A, on suppose que le véhicule est assez éloigné de Mars pour pouvoir négliger l’énergie gravitationnelle. En déduire l’expression de l’énergie mécanique et la nature de la trajectoire de(s). Le justifier sur un graphique.
Montrer que le moment cinétique se conserve et définir la constante des aires C. Calculer C en fonction de \(v_A\) et b.
Sachant que ma trajectoire d’approche est tangente au cercle de rayon \(\alpha r_M\) en B, calculer \(v_B\) (vitesse en B) en fonction de \(v_A, r_M, \alpha\) et \(b\).
Exprimer le paramètre d’impact b, en fonction de \(r_M, v_A, M_M\) et \(\alpha\). A.N.: \(\alpha = 3\).
Déterminer la distance minimale \(b_m\) pour que le véhicule évite la surface de Mars.
Déterminer la vitesse \(v_c\) d’un objet sur l’orbite circulaire de rayon \(3 r_m\) ainsi que sa période de révolution en fonction des données.
Au point B (avec \(\alpha = 3\)), on veut que le véhicule passe sur l’orbite circulaire de rayon \(3 r_M\). Déterminer la variation de vitesse \(\Delta v_c\) à communiquer au véhicule en fonction des données.
Point utile pour cet exercice
\(\Longrightarrow\) Lois de Kepler.
\(\Longrightarrow\) Trajectoire hyperbolique.
\(\Longrightarrow\) Energie mécanique.
\(\Longrightarrow\) Mobile à l’infini.
\(\Longrightarrow\) Moment cinétique.
Comète à trajectoire parabolique
La comète Arend-Roland est une comète à trajectoire d’excentricité e estimée à 1,0002. On assimilera la trajectoire à une parabole d’excentricité e=1. La comète est passée à son périhélie, le 8 avril 1857, à \(r_P = 0,316 \rm{u.a.}\) du soleil.
Calculer le paramètre de la trajectoire.
Exprimer le paramètre p de la conique en fonction de la constante des aires C, de G et la masse du soleil \(M_S\). En déduire la vitesse de la comète au périhélie.
Montrer que l’on peut exprimer la vitesse angulaire \(\dot \theta\) en fonction de la constante des aires C et du paramètres p de la parabole par: \(\dot \theta = C\frac{{(1+ \cos \theta)}^2}{p^2}\). En quel point est prise l’origine \(\theta=0\)?
On note \(t_0\) l’instant de passage au périhélie P. Montrer alors que l’on obtient le temps de passage pour le point d’angle \(\alpha\) avec:
Pour calculer cette intégrale, on effectue le changement de variable \(x = \tan \frac{\theta}{2}\). En déduire l’expression: \(t = t_0 + \frac{p^2}{2C} (X + \frac{X^3}{3})\) où \(X = \tan \frac{\alpha}{2}\).
(Analyse numérique) La comète a été découverte par les astronomes belges Sylvain Arend et Georges Roland le 8 novembre 1856. A quelle distance se trouvait-elle du Soleil?
Point utile pour cet exercice
\(\Longrightarrow\) Lois de Kepler.
\(\Longrightarrow\) Trajectoire parabolique.
\(\Longrightarrow\) Energie mécanique.