6.1.2.4. Types d’actions

On distinguera deux types d’actions:

• les actions à distance : en général associées à des actions ponctuelles usuelles comme la gravitation, la pesanteur ou l’interaction électromagnétique. Elles agissent en volume (intégration volumique)

• les actions de contact : résultante d’actions ponctuelles microscopiques de courte distance (Van der Waals principalement), elles n’ont en général pas d’expression connues (sauf cas de non frottements) mais peuvent contraindre de le mouvement. On parle de liaison.

6.1.2.4.1. Actions à distances

Actions volumiques

Les actions à distance sont en général des actions volumiques (si elle s’exercent à distance, tous les points du solide sont a priori concernés). La force et le moment résultant découle alors d’une intégration en volume (triple intégrale). Il n’est pas nécessaire de savoir (pour l’instant) calculer ces intégrales.

• En général, la force résultante se calcule à partir de l’expression usuelle des forces ponctuelles associées aux actions ponctuelles usuelles (gravitation… )

• En général, on donne (ou il doit être connu), un point où le moment résultant est nul (appelé parfois par abus de langage “point d’application”).

Important

Action de la pesanteur

Cas d’un champ de psanteur uniforme. L’action de la pesanteur sur un corps a alors :

• pour force résultante \(\overrightarrow{P} = M\overrightarrow{g}\)

• un moment résultant nul en un point appelé centre de gravité. Il est confondu avec le centre d’inertie pour un champ uniforme.

Ecriture du torseur

Le torseur de l’action de la pesanteur doit donc être parfaitement connu au centre de gravité G ET en tout point A de l’espace:

\[\begin{split} \mathcal{T}_G(\mathcal{A_{pesanteur \to \Sigma}}) = \begin{cases} &\overrightarrow{F}_{pesanteur \to \Sigma} = m \overrightarrow{g}\\ &\overrightarrow{M}_{G,pesanteur \to \Sigma} = 0 \end{cases} \Longrightarrow \mathcal{T}_A(\mathcal{A_{pesanteur \to \Sigma}}) = \begin{cases} &\overrightarrow{F}_{pesanteur \to \Sigma} = m \overrightarrow{g}\\ &\overrightarrow{M}_{A,pesanteur \to \Sigma} = 0 + \overrightarrow{AG} \wedge \overrightarrow{F}_{pesanteur \to \Sigma} \end{cases} \end{split}\]

Démonstration

On traite le cas discret.

\[ \overrightarrow{P} = \sum\limits_{i} (m_i \overrightarrow{g}) = \sum\limits_{i} (m_i) \overrightarrow{g} = M \overrightarrow{g} \]

Et :

\[ \overrightarrow{M_G}(Poids) = \sum\limits_{i} (\overrightarrow{GM_i} \wedge m_i \overrightarrow{g}) = \sum\limits_{i} (m_i \overrightarrow{GM_i}) \wedge\overrightarrow{g} = M \overrightarrow{GG} \wedge \overrightarrow{g} = \overrightarrow{0} \]

6.1.2.4.2. Actions de contact

Les actions de contact sont en général surfacique: on va sommer les actions ponctuelles en surface (double intégale) en se restreignant évidemment à la surface de contact ! On ne cherchera pas à calculer ces intégrales. L’expression des caractéristiques de ces actions de contacts se fait de deux manières (cf. en ligne).

Types d’actions de contact

• Cas d’action d’un fluide (liquide ou gaz). Comme on va le voir, on dispose souvent d’expression de la résultante des forces. En première année, on utilise principalement ces actions dans le cadre d’une modélisation ponctuelle du système mécanique de sorte que le moment résultant n’est pas donné (l’action devenant par modélisation… ponctuelle).

• Cas d’action d’un solide (on parle de liaison). Dans le cadre du programme, les caractéristiques:

  • sont inconnues et ne peuvent être déterminées que par l’utilisation de théorème (comme le PFD (ou plutôt TRD… ) qui permet de déterminer certaines composantes des forces et moments résultants.

  • possèdent des composantes nulles par hypothèse (cas d’absence de frottements)

  • sont établies ou encadrées (inégalité) grâce aux lois de Coulomb (cf. suite)

On rappelle que la composante normale correspond à une “réaction de non interpénétration” et que la composante tangentielle correspond aux frottements.

Important

Rappel : Composante tangentielle et composante normale

En un point de contact M entre le système et le solide/fluide (qu’on appellera \(\Sigma_{ext}\)), l’action ponctuelle (modélisée par la force \(\overrightarrow{F}(M)\) peut-être décomposée en deux composantes):

• une composante normale à la surface de contact \(\overrightarrow{F_{\perp}}(M)\)

• une composante tangentielle à la surface de contact \(\overrightarrow{F_{//}}(M)\)

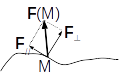
Il n’y a pas d’expression simple a priori de cette action ponctuelle qui dépend de la géométrie au point de contact mais aussi du reste du contact, des autres actions qui s’appliquent sur les deux systèmes, de la nature des matériaux qui forment le système…

On peut néanmoins obtenir plusieurs informations sur la force et moment résultant de l’action globale suivant les cas (solide ou fluide, géométrie du contact… ). C’est ce que nous ferons par la suite.

6.1.2.4.2.1. Action d’un fluide

6.1.2.4.2.1.1. Modélisation de l’action d’un fluide (en ligne)

Interprétation des composantes

La composante normale de l’action d’une fluide est appelé force(action) de pression. Un chapitre complet sera destiné à l’étude des forces de pression. Dans le cadre actuel de la mécanique, on se bornera à citer son existence.

La composante tangentielle de l’action d’un fluide correspond aux frottements fluides. Comme il sera expliqué en deuxième année, cette composante tangentielle est toujours fonction du différentiel du vitesse au voisinage du point de contact. En première année, le fluide étant supposé au repos loin du système mobile, cela ramène à dire que la composante tangentielle est fonction de la vitesse du système étudié dans le référentiel d’étude. On distingue deux cas:

• le système est en translation dans le fluide. On travaille alors (dans le cadre du programme de première année) avec la force résultante exercée par le fluide appelée force de frottements. Celle-ci est toujours opposée à la vitesse. Il existe plusieurs expressions qui seront discutées par la suite.

• le système est en rotation autour d’un axe fixe et donc en rotation par rapport au fluide. On donne alors le moment résultant de l’action du fluide sur le système calculé sur l’axe de rotation. Correspondant à des frottements, ce moment s’oppose à la vitesse angulaire \(\dot \theta\) du fluide. En général (cas dit laminaire), le moment sur l’axe a pour expression \(- K \dot \theta\).

Type de régimes

La force de frottements fluide va dépendre du comportement du fluide qui de la géométrie du système (même si quand on passe à une modélisation ponctuelle du système cette dépendance reste) et à sa vitesse par rapport au fluide ainsi qu’à la viscosité du fluide.

On distingue deux types de régimes extrêmes: le régime laminaire (aux faibles vitesses) où l’écoulement du fluide épouse la forme de l’obstacle (ici le système mobile) et le régime turbulant (aux fortes vitesses) où l’écoulement du fluide possède un caractère tourbillonnaire (vortex). La transition du premier régime au second régime n’est pas brusque et des phénomènes très particuliers peuvent se produire pour des vitesses intermédiaires (ces cas ne seront pas étudiés en classe préparatoire).

6.1.2.4.2.1.2. Expression de la force de frottements fluides

Important

Force de frottements fluide

• Cas laminaire : Aux faibles vitesses, la force ou le moment résultant de frottements fluides est proportionnelle à la vitesse du fluide.

  • Pour un système en translation : \(\overrightarrow{F} = - \lambda \overrightarrow{v_{systeme/fluide}}\).

  • Dans le cas d’un système en rotation au tour d’un axe fixe : \(M_{axe}(fluide) = - K \dot \theta\) où \(\dot \theta\) est la vitesse angulaire du solide autour de l’axe (fluide supposé au repos)

• Cas turbulent : Aux fortes vitesses, la force de frottements fluides est proportionnelle au carré de la vitesse du fluide: \(\overrightarrow{F} = -k \left \| v\right \| \overrightarrow{v}\). Cette expression est valable pour un système en translation. Le cas d’un système en rotation ne sera pas traité.

Ecriture du torseur

Le torseur de l’action d’un fluide aura donc plusieurs formes possibles suivant les cas. Dans tous les cas, plusieurs composantes du torseurs sont inconnues et ne sont souvent pas utiles:

• Solide en translation:

\[\begin{split} \mathcal{T}_A(\mathcal{A_{fluide \to \Sigma}}) = \begin{cases} &\overrightarrow{F}_{fluide \to \Sigma} = - \lambda \overrightarrow{v} + ? \textrm{ ou } - k v \overrightarrow{v} + ?_{normale}\\ &\overrightarrow{M}_{A,fluide \to \Sigma} = ? \end{cases} \end{split}\]

Le \(?_{normale}\) correspond à la résultante des composantes normales qui est a priori inconnue. Un chapitre sera dédié à son étude par la suite. Pour l’instant, il n’interviendra pas dans les études, on pourra considérer sa projection dans la direction du mouvement comme nulle. Le \(?\) correspond au moment dont l’expression n’est pas à connaître et qui n’intervient généralement pas dans l’étude (il arrive d’ailleurs fréquemment qu’il soit omis dans l’expression de la force résultante).

• Solide en rotation autour d’un fixe \(Oz\) (on repère la rotation par la position \(\theta\) d’un point du solide):

\[\begin{split} \mathcal{T}_A(\mathcal{A_{fluide \to \Sigma}}) = \begin{cases} &\overrightarrow{F}_{fluide \to \Sigma} = ?\\ &\overrightarrow{M}_{A,fluide \to \Sigma} = - K \dot \theta \overrightarrow{e_z} + ?_{\perp} \end{cases} \end{split}\]

Le \(?_{\perp}\) correspond à moment résultant dans les directions perpendiculaires à l’axe de rotation. Il n’influe donc pas sur le mouvement et son expression n’est donc pas utile (il arrive d’ailleurs fréquemment qu’il soit omis dans l’expression du moment résultant). Le \(?\) correspond à la résultante des action dont l’expression n’est pas à connaître et qui n’intervient généralement pas dans l’étude.

6.1.2.4.2.2. Action de contact solide

6.1.2.4.2.2.1. Lois phénoménologiques de Coulomb

Il n’y a pas de modèle théorique complet permettant de déterminer les actions de contact solide. Il existe par contre une loi phénoménologique (déduite de l’expérience) qui permet de les modéliser. Plus précisément, on va, au niveau des actions ponctuelles, relier la composante normale et la composante tangentielle.

Des relations équivalentes entre les moments associés aux frottements et aux actions normales existent aussi pour des solides en rotation.

Important

Rappel : Lois phénoménologiques de Coulomb

En un point de contact solide-solide, la force de contact \(\overrightarrow{R}\) se décompose en deux composantes, l’une tangentielle \(\overrightarrow{R_T}\) et l’autre normale \(\overrightarrow{R_N}\) (\(\overrightarrow{R} = \overrightarrow{R_N} + \overrightarrow{R_T}\)). On déduit expérimentalement les comportements suivants:

• La composante normale est telle qu’elle empêche l’interpénétration des systèmes (contrainte cinématique). Elle est dirigée vers l’intérieur du solide qui subit l’action. Son annulaion signifie la perte de contact.

• La composante tangentielle a un comportement qui dépend de l’état relatif des deux solides:

  • en cas d’immobilité relative des deux solides, l’action complète est telle qu’elle permet l’immobilité relative (somme des forces nulle ET somme des moments nuls si l’on est dans un référentiel galiléen). La composante tangentielle est de norme nécessairement inférieure à \(\left \| \overrightarrow{R_T}\right \| < \mu_S \left \| \overrightarrow{R_N}\right \|\) où \(\mu_S\) est appelé coefficient de frottement statique. Lorsque cette condition est mise en défaut, alors le système se met en mouvement.

  • en cas de mouvement relatif des deux solides (on dit qu’il y a glissement au point M), la composante tangentielle s’oppose à la vitesse relative au point M. Sa norme est égale à \(\left \| \overrightarrow{R_T}\right \| = \mu_D \left \| \overrightarrow{R_N}\right \|\) où \(\mu_D\) est appelé coefficient de frottement dynamique.

• Quelque soit le système, \(\mu_D < \mu_S\), c’est-à-dire qu’il est plus facile de maintenir un solide en mouvement par rapport à un autre solide malgré les frottements que de mettre en mouvement le même solide.

Attention

Les relations précédentes ne concernant a priori que les forces ponctuelles. Le passage aux actions globales dépend de la géométrie de la liaison.

6.1.2.4.2.2.2. Liaisons normalisée et géométrie

Liaison et géométrie

Les caractéristiques d’une action de contact solide résulante vont dépendre de la géométrie de la surface de contact. En effet, certaines géométries vont empêcher certains mouvements. Cela signifie que la force résultante et le moment résultant peuvent être non nuls pour empêcher ces mouvements.

Par exemple, deux solides \(\Sigma_1\) et \(\Sigma_2\) dont la surface de contact est une sphère (ou portion de sphère) ne peuvent que tourner l’un par rapport à l’autre, les mouvements de translation relatifs (sans perte de contact) sont impossibles. Si une autre action \(\mathfrak{A}_{ext \to \Sigma_1}\) extérieur tend à faire translater le solide \(\Sigma_1\), alors l’action de \(\Sigma_2\) sur \(\Sigma_1\) va tendre à s’opposer à l’action \(\mathfrak{A}_{ext \to \Sigma_1}\).

A l’inverse la géométrie de la surface de contact va laisser des mouvements possibles, on parle de degré de liberté de la liaison. Dans l’exemple précédente, toutes les rotations sont possibles.

On ne peut a priori déduire des degrés de liberté des informations sur la force résultante ou sur le moment résultante.

Par contre, si la liaison est sans frottements (on dit que la liaison est parfaite), alors il vient que certaines composantes des éléments modélisant l’action seront nuls: les éléments qui s’opposent au mouvement selon les degrés de liberté. Dans l’exemple précédent, les éléments s’opposant à la rotation relative des solides sont nuls si la liaison est sans frottements: c’est le moment résultant exprimé au centre de la sphère de contact.

Liaisons normalisée En général, on travaille avec des géométries simples et usuelles pour les surfaces de contact. On parle de liaison normalisée (celle présentée précédemment est la liaison rotule ou sphérique). Ces liaisons ont été vues en SI. En physique les seules à connaître sont la liaison pivot et la liaison glissière.

Torseur d’une liaison

Néanmoins, il est important de comprendre qu’a priori, le torseur dynamique d’une liaison est… quelconque et les composantes ne sont pas connues. Par exemple, dans un système de coordonnées cartésiennes, le torseur ressemblerait à les ? en indice donne les composantes qu’on ne connait pas:

\[\begin{split} \mathcal{T}_A(\mathcal{A_{solide \to \Sigma}}) = \begin{cases} &\overrightarrow{F}_{solide \to \Sigma} = F_{x,?}\overrightarrow{e_x} + F_{y,?}\overrightarrow{e_y} + F_{z,?}\overrightarrow{e_z}\\ &\overrightarrow{M}_{A,solide \to \Sigma} = M_{A,x,?}\overrightarrow{e_x} + M_{A,y,?}\overrightarrow{e_y} + M_{A,z,?}\overrightarrow{e_z}\\ \end{cases} \end{split}\]

… … … On n’est pas très avancé (on rappelle, cf. SI, que les liaisons donnent par contre beaucoup d’informations sur les aspects cinématiques en interdisant certaines mouvements).

Néanmoins, des caractéristiques supplémentaires permettent de connaître certaines composantes ou des relations entre composantes. Par exemple:

• si l’on considère que la liaison est sans frottements (liaison parfaite), alors certaines composantes seront nulles (faire le parallèle avec la composante tangentielle nulle en mécanique du point).

• si l’on suppose valides les lois de Coulomb, alors en identifiant les composantes “tangentielles” et “normales” résultantes, on peut relier certaines composantes (leurs normes).

6.1.2.4.2.2.2.1. Liaison glissière

Cette liaison ne permet au mobile qu’un mouvement de translation. Dans ces cas là, on s’intéresse alors principalement à la résultante des forces et pas au moment. Ce dernier est donc souvent inconnu (pas nul) sans que cela soit un problème.

Au niveau de la force, on distingue alors la composante tangentielle des composantes normales. On peut alors utiliser, suivant les problèmes, l’hypothèse de non frottements ou les lois de Coulomb.

En terme de torseur

Si l’on choisit l’axe Ox d’un repère cartésien comme l’axe de la glissière, il vient:

\[\begin{split} \mathcal{T}_A(\mathcal{A_{glissiere \to \Sigma}}) = \begin{cases} &\overrightarrow{F}_{glissiere \to \Sigma} = \underbrace{F_{x}\overrightarrow{e_x}}_{\textrm{composante tangentielle, agit sur la translation (frottements/non glissement), connu ou loi de Coulomb}} + \underbrace{F_{y,?}\overrightarrow{e_y} + F_{z,?}\overrightarrow{e_z}}_{\textrm{composante normale, inconnue}}\\ &\overrightarrow{M}_{A,glissiere \to \Sigma} = ?\\ \end{cases} \end{split}\]

Des éléments communs concernant la résultante des forces s’obtiennent pour une liaison plan-plan (on a par contre deux composantes tangentielles et une composante normale).

6.1.2.4.2.2.2.2. Liaison pivot

Important

Liaison pivot

La liaison pivot est une liaison où le seul degré de liberté est la rotation entre les deux solides. Elles est réalisée par une surface de contact cylindrique (qui permet une rotation suivant UN axe) fermé latéralement (pour empêcher la translation suivant l’axe de rotation).

En physique, on travaille en générale avec un solide mobile (le rotor) en liaison pivot avec le bati (stator - en général le référentiel associé au bati est un référentiel galiléen en physique).

Caractéristiques d’une liaison pivot

On rappelle que les caractéristiques modélisant une action globale sont la force et le moment résultant exprimé en un point. En général, pour une liaison pivot, on essaie d’exprimer le moment de la liaison sur un point de l’axe de rotation de la liaison.

A priori, toutes les composantes de la force et du moment résultant peuvent être non nulles. On distingue néanmoins:

• les composantes de la force résultante qui peuvent être non nuls pour empêcher les translations. Elles s’opposent à la force résultante des autres actions sur le rotor.

• les composantes du moment résultant dans les directions perpendiculaires à l’axe de rotation empêchent les rotations suivant les autres axes. Elles s’opposent au moment des autres actions sur ces mêmes axes.

• la composante du moment résultant sur l’axe de rotation. Elle agit sur le (seul) mouvement du rotor à savoir le mouvement de rotation suivant l’axe. Elle peut a priori avoir un effet moteur ou résistant suivant l’expression de ce moment.

Erreurs classiques

Attention, la nullité/non-nullité du moment sur l’axe n’est pas liée à l’orientation de la force résultante. On rappelle qu’il n’y a pas de lien directe entre force résultante et moment résultant.

De même seul le moment suivant l’axe de rotation est nul dans le cas sans frottements. Les moments suivant un axe quelconque (perpendiculaire ou même parallèle mais non confondu avec l’axe de rotation) sont a priori non nulle. De même la force résultante est a priori non nulle.

En terme de torseur

En terme de torseur, on choisira donc un système de coordonnées cylindriques d’axe Oz l’axe de rotation de la liaison et on choisit un point de l’axe pour exprimer le moment. On peut alors interpréter les composantes de la force résultante et du moment résultant:

\[\begin{split} \mathcal{T}_{A \in axe}(\mathcal{A_{pivot \to \Sigma}}) = \begin{cases} &\overrightarrow{F}_{pivot \to \Sigma} = \underbrace{F_{x,?}\overrightarrow{e_x} + F_{y,?}\overrightarrow{e_y} + F_{z,?}\overrightarrow{e_z}}_{\textrm{empêche toute translation}}\\ &\overrightarrow{M}_{A,pivot \to \Sigma} = \underbrace{M_{A,x,?}\overrightarrow{e_x} + M_{A,y,?}\overrightarrow{e_y}}_{\textrm{empêche toute rotation autre qu autour de Oz}} + \underbrace{M_{A,z}\overrightarrow{e_z}}_{\textrm{agit sur la rotation, connu}}\\ \end{cases} \end{split}\]

Important

Liaison pivot parfaite

Une liaison pivot parfaite est une liaison pivot sans frottements, le moment résultant de la liaison sur l’axe de rotation est nulle.

Explication

Dans une liaison pivot, la surface de contact est un cylindre. S’il n’y a pas de frottements, alors il n’y a pas de composantes tangentielles pour chaque action ponctuelles de contact.

Dans le cas des surfaces planes extrêmes, la force ponctuelle est donc suivant l’axe de rotation: son moment sur l’axe est nul.

Dans le cas de la surface latérales en forme de cylindre, la force ponctuelle est dirigée vers l’axe de rotation: son moment sur l’axe est nul.

Il vient que le moment résultant sera nul.

6.1.2.4.2.2.3. Action d’un fil de torsion

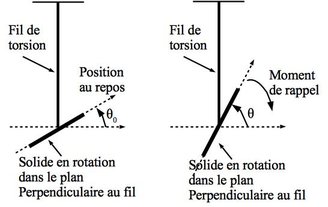
Fil de torsion Un fil de torsion est un fil dont la section n’est pas négligeable et qui peut se tordre suivan son axe. Son élasticité implique qu’il va tendre à se détendre exerçant pour cela un moment à ses extrémités proportionnel à l’angle de torsion.

Important

Action d’un fil de torsion

Soit un fil pouvant se tordre suivant son axe. On suppose qu’il ne flambe pas. Pour un angle de torsion \(\theta - \theta_0\) du fil, ce dernier exerce à ses extrémités une action dont le moment suivant l’axe de torsion est:

\[ \Gamma_{axe} = - C \left(\theta - \theta_0\right) \]

où C est appelée constante de torsion du fil.

On remarquera qu’une telle action est sembable à une action de rappel élastique. Pour le ressort, le rappel se fait suivant ue translation. Ici le rappel concerne une rotation.

L’angle \(\theta\) repère la torsion du fil. La présence de l’angle \(\theta_0\) permet de placer l’origine des angles en un point où le fil est déjà tordu. Cela peut-être utile lorsque l’on étudie plusieurs fil de torsion.

On parle de moment de rappel ou par abus de langage de couple de rappel.

En terme de torseur

En terme de torseur, on part donc du torseur de la liaison pivot quelconque en un point de l’axe et on précise le moment sur l’axe.

\[\begin{split} \mathcal{T}_{A \in axe}(\mathcal{A_{torsion \to \Sigma}}) = \begin{cases} &\overrightarrow{F}_{torsion \to \Sigma} = \underbrace{F_{x,?}\overrightarrow{e_x} + F_{y,?}\overrightarrow{e_y} + F_{z,?}\overrightarrow{e_z}}_{\textrm{empêche toute translation}}\\ &\overrightarrow{M}_{A,torsion \to \Sigma} = \underbrace{M_{A,x,?}\overrightarrow{e_x} + M_{A,y,?}\overrightarrow{e_y}}_{\textrm{empêche toute rotation}} - C \theta_{torsion} \overrightarrow{e_z}\\ \end{cases} \end{split}\]