Entrainement : Oscillateurs

Etude d’un portrait de phase

On fait l’étude d’un oscillateur M de masse \(m = 0.2\rm{kg}\) astreint à se déplacer suivant l’axe Ox de vecteur unitaire \(\overrightarrow{u_x}\). Il est soumis aux forces suivantes:

• la force de rappel d’un ressort de caractéristiques \((k,l_0)\).

• une force de frottements visqueux linéaire de coefficients de frottement \(\lambda\)

• une force constante \(\overrightarrow{F_C} = F_C \overrightarrow{u_x}\).

Le portrait de phase \((X(t); V(t) = \frac{\rm{d}X}{\rm{dt}}(t)) \)de l’oscillateur étudié est donné sur la figure Figure E.6. On souhaite pouvoir en tirer les valeurs des différents paramètres de l’oscillateur.

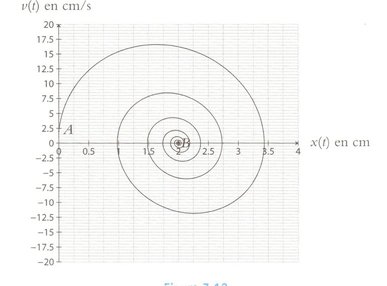
On donne les abscisses correspondant aux croisements de la trajectoire de phase avec l’axe des abscisses:

Croisement	1	2	3	4	5
t(s)	0.31	0.65	0.97	1.3	1.62

1 Établir l’équation différentielle du mouvement de M et la mettre sous la forme: \(\ddot x + \frac{\omega_0}{Q} \dot x + \omega_0^2 x = \omega_0^2 X_0\) où x est l’allongement du ressort (par rapport à \(l_0\)). Les grandeurs \(w_0, Q\) et \(X_0\) sont à exprimer en fonction des données.

1. Dans le cas d’une solution pseudo-périodique, exprimer \(x(t)\): on définira le temps de relaxation énergétique \(\tau\) et la pseudo-période \(\Omega\) que l’on exprimera en fonction de \(\omega_0\) et \(Q\).

2. Déterminer la vitesse de l’élongation au début et à la fin du mouvement.

3. Déterminer la vitesse maximale atteinte ainsi que l’élongation maximale.

4. En déduire la pseudo-période T et la pseudo-pulsation \(\Omega\).

5. On définit le décrément logarithmique par: \(\delta = \frac{1}{n} \ln \left(\frac{x(t) - x_B}{x(t+nT) - x_B}\right)\) où \(x(t)\) et \(x(t+nT)\) correspondent aux élongations aux temps \(t\) et \(t + nT\) et \(x_B\) correspond à l’élongation finale de M. Exprimer \(\delta\) en fonction de T et \(\tau\). En choisissant une valeur de n la plus grande possible pour les données dont on dispose déterminer \(\delta\) puis \(\tau\).

6. Déduire des résultats précédents le facteur de qualité Q et la pulsation propre \(\omega_0\).

7. Déterminer la raideur du ressort k, le coefficient de frottement \(\lambda\) et la force \(F_C\) sachant que \(l_0 = 1\rm{cm}\).

Point utile pour cet exercice

• \(\Longrightarrow\) Oscillateur amorti.

• \(\Longrightarrow\) Régime pseudo-périodique.

• \(\Longrightarrow\) Portrait de phase.

• \(\Longrightarrow\) Decrément logarithmique.

Amortisseur

On considère l’amortisseur d’un véhicule. Chaque roue supporte un quart de la masse de la voiture assimilé (la quart de voiture) à un point M de masse \(m=500\rm{kg}\) et relié à la voiture par un amortisseur dont le ressort a une constante de raideur \(k = 2,5 \times 10^{4} N.m^{-1}\).

Le point M subit aussi un frottement visqueux \(\overrightarrow{f} = - \lambda \overrightarrow{v}\) où \(\overrightarrow{v}\) est la vitesse verticale de M par rapport au sol. On donne \(\lambda = 5 \times 10^{3} \rm{kg.s^{-2}}\). Le véhicule franchit à vitesse constante un défaut de chaussée de hauteur h=5cm. Son inertie est suffisante pour qu’il ne se soulève pas immédiatement mais acquiert une vitesse verticale \(v_0 = 0,5 \rm{m.s^{-1}}\). On pose \(\alpha = \lambda/m\). On note \(Z_i\) la cote du point M avant le passage du défaut (on suppose qu’il n’y a pas de mouvement vertical avant le défaut).

1. On note \(Z(t)\) la cote du point M. Établir l’équation différentielle pour Z après le passage de l’obstacle. On introduira la grandeur \(\alpha\).

2. Déterminer \(Z(t)\) en fonction des données. Calculer numériquement \(\alpha\) et \(\Omega\) et en déduire qu’on peut simplifier légèrement l’expression de \(Z(t)\). On gardera cette simplification par la suite.

3. Les passagers sont sensibles à l’accélération verticale de la voiture. Calculer sa valeur maximale.

4. Il faut éviter des oscillations susceptibles de provoquer chez les passagers le mal des transports, en se plaçant dans les conditions critiques. Pour quelle masse par roue est-ce réalisé, \(k\) et \(\lambda\) restant inchangés?

Point utile pour cet exercice

• \(\Longrightarrow\) Oscillateur amorti.

• \(\Longrightarrow\) Régime pseudo-périodique.

• \(\Longrightarrow\) Ressort.

Frottements solides

On considère un mobile M de masse m se déplaçant selon un axe horizontal (Ox) et assimilé à un point matériel. Ce mobile est soumis à une force de rappel \(\overrightarrow{f_R} = -kx \overrightarrow{e_x}\) (longueur à vide nulle) et à une force de frottement solide de coefficient de frottement dynamique \(f_D\) et statique \(f_S\). Pour simplifier le problème, on prendra ici \(f_D = f_S\) et on parlera de coefficient de frottement solide. On pose le mobile M en un point d’abscisse \(x_0\) sans vitesse initiale.

1. Montrer que pour que le mobile se mette en mouvement, il faut que \(\vert x_0 \vert > x_{m0}\) où \(x_{m1}\) est à exprimer en fonction de f,m,g et k.

2. On suppose que \(x_0 > x_{m0}\). Montrer que le mouvement du solide se décompose en plusieurs phase. Déterminer \(x_1(t)\), abscisse du mobile au cours de la première phase.

3. Déterminer l’instant \(t_1\) pour lequel cette première phase s’arrête. A quelle condition le mobile s’arrête-il complètement à la fin de la première phase? On exprimera cette condition sous la forme \(x_{m0} < \vert x_0 \vert < x_{m1}\).

4. Dans le cas où on est à la limite d’immobilisation complète du mobile à la fin de la première phase, déterminer le travail de la force de frottement pendant cette phase et faire un bilan énergétique.

5. On suppose maintenant que le mobile ne s’immobilise pas définitivement à \(t_1\). Déterminer \(x_2(t)\) abscisse du mobile pendant la seconde phase et en déduire la pseudo-période des oscillations du mobile.

On suppose que le mobile réalise N oscillations complètes avant de s’arrêter à \(x_{fin} = a\). On note m=2N et \(x_i(t)\) l’abscisse du mobile au cours de la i-ème demie-période (soit la i-ème phase du mouvement). i varie donc de 1 à m. On note aussi \(t_i\) l’instant pour lequel se termine la i-ème phase du mouvement. Le temps \(t_m\) est donc le temps pour lequel le mouvement s’achève complètement. On note enfin \(X_i\) l’abscisse atteinte à la fin de la i-ème oscillation. On a donc \(X_m = a\).

6. Quelles conditions vérifient les \(X_i\) pour \(1 \leq i \leq m-1\)?

7. Établir une relation de récurrence entre \(X_i\) et \(X_{i+2}\). En déduire une relation entre \(X_m\) et \(x_0\) puis \(x_0\) en fonction de a.

8. Comparer le comportement de cet oscillateur avec l’oscillateur amorti par frottement fluide et tracer \(x(t)\).

Point utile pour cet exercice

• \(\Longrightarrow\) Oscillateur amorti.

• \(\Longrightarrow\) Frottements solides.

• \(\Longrightarrow\) Théorème de l’énergie mécanique.

Elasticité d’une fibre de verre

Le verre est un matériau très dur. On peut toutefois le déformer légèrement sans le casser: on parle d’élasticité. Récemment, des expériences de biophysique ont été menées pour étudier l’ADN. Le capteur utilisé était simplement une fibre optique en silice amincie à l’extrémité de laquelle on accroche un brin d’ADN. L’expérience consistait à suivre la déformation de flexion de la fibre. La masse volumique du verre est \(\rho=2500\rm{kg.m{-1}}\).

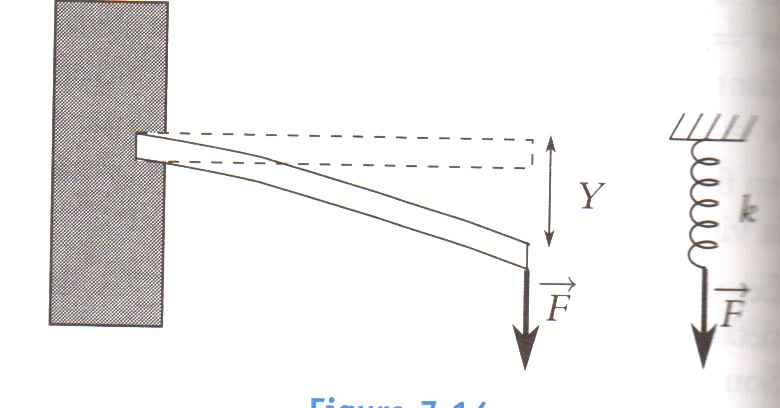
La fibre de verre de longueur \(l\) et de diamètre \(d\) est encastrée horizontalement dans une paroi immobile. Au repos, la fibre est horizontale (on néglige le poids). Quand on applique une force verticale \(F\) (on supposera que \(F\) reste verticale tout au long de l’expérience) à l’extrémité libre de la fibre, celle-ci est déformée. L’extrémité est déplacée verticalement d’une distance Y que l’on appelle la flèche. La flèche Y est donnée par la relation suivante: \(Y = \frac{7l^3 F}{Ed^4}\) où \(E\) est appelé module d’Young du verre. Pour les applications numériques, on prendra pour le module d’Young \(E=7.10^{10} S.I\).

1. Quelle est l’unité S.I. du module d’Young?

2. En considérant uniquement la force F, montrer que l’on peut modéliser la fibre de verre par un ressort de longueur à vide nulle et de constante de raideur k dont on donnera l’expression analytique en fonction de \(E, d\) et \(l\).

3. Calculer numériquement k pour une fibre de longueur \(l=7\rm{mm}\) et de diamètre \(d = 10 \rm{\mu m}\).

4. Donner (à la justifiant) l’expression de l’énergie potentielle élastique d’un ressort de longueur à vide nulle, de constante de raideur k lorsque sa longueur est l. En reprenant l’analogie du ressort, quelle est alors l’énergie potentielle élastique de la fibre de verre lorsque la flèche vaut Y?

Point utile pour cet exercice

• \(\Longrightarrow\) Oscillateur amorti.

• \(\Longrightarrow\) Unités et dimensions.

• \(\Longrightarrow\) Energie potentielle.

Piscine à vagues

Pour créer des vagues dans une piscine, on fait effectuer des oscillations verticales à une masse immergée sur un côté du bassin. Soit une masse M homogène de masse volumique \(\rho\) et de volume V plongée dans l’eau de masse volumique \(\rho_{eau}\). Cette masse est suspendue à un ressort de raideur k et de longueur à vide \(l_0\) accroché à son extrémité en un point A. On note Oz l’axe vertical vertical passant par A et orienté vers le bas et on prend O comme origine. A l’équilibre, la masse M est située en z = h. On se place dans le référentiel terrestre supposé galiléen. On suppose dans un premier temps que A est immobile et A=O.

1. On suppose d’abord que la masse M est dans l’air. On ne tient pas compte des frottements.

   1. Etablir la condition d’équilibre de la masse M dans l’air.

   2. En déduire l’équation différentielle du mouvement en z de la masse M si le mouvement s’effectue dans l’air.

   3. Quelle est la nature du mouvement? On donnera les expressions de ses principales caractéristiques.

2. Du fait que le mouvement a lieu dans l’eau, comment doit-on modifier les équations précédentes (on ne tiendra toujours pas compte des frottements).

3. On tient compte désormais des frottements visqueux: \(\overrightarrow{f} = - \alpha \overrightarrow{v}\).

   1. Déterminer la nouvelle équation différentielle vérifiée par z.

   2. Dans le cas d’un amortissement faible et en supposant que \(z(0) = h_1 > h\) et \(\dot z(0) = 0\), déterminer \(z(t)\)?

4. A l’aide d’un piston, on impose un mouvement sinusoïdal au point de suspension A du ressort. Cela revient à appliquer une force \(\overrightarrow{f} = a M \omega_{2}^2 \cos(\omega_2 t)\overrightarrow{u_z}\) à la masse M. On pose \(Z = z- h\) l’écart à la position d’équilibre.

   1. Donner la nouvelle équation différentielle du mouvement.

   2. Dans le cas d’un amortissement faible, justifier que la solution complète pour \(Z(t)\) serait somme de 2 termes dont on précisera le sens mais qu’on ne calculera pas.

   3. A partir de l’équation différentielle, déterminer l’expression de l’amplitude complexe Z des oscillations en régime sinusoïdal forcé. On utilisera les grandeurs: \(a, x = \frac{\omega}{\omega_0}, \tau = \frac{M}{\alpha}, \omega_0 = \sqrt{\frac{k}{M}}\).

   4. On se place en régime permanent établi. Déterminer les deux conditions nécessaires pour qu’on puisse avoir des oscillations d’amplitude supérieure à a, l’une portant sur la valeur minimale de la masse M et l’autre sur l’intervalle de pulsations à utiliser.

   5. Quelle est alors la pulsation pour laquelle l’amplitude est la plus grande?

   6. Donner l’expression de l’amplitude correspondante en fonction de a, M, k et \(\alpha\).

Point utile pour cet exercice

• \(\Longrightarrow\) Oscillateur harmonique.

• \(\Longrightarrow\) Oscillateur amorti.

• \(\Longrightarrow\) Oscillateur forcé.

• \(\Longrightarrow\) Réponse en position.

Vibration d’une molécule diatomique

La molécule HCl est modélisée, selon un axe fixe, par deux masses ponctuelles distantes de r. Puisque l’atome de chlore est beaucoup plus lourd que celui d’hydrogène, il peut être considéré comme fixe. Seul le noyau d’hydrogène de masse m est alors susceptible de se déplacer, il subit l’énergie potentielle d’interaction:

\[ E_p(r) = \frac{C}{r^n} - \alpha \frac{e^2}{4 \pi \epsilon_0 r} \]

où C, \(\alpha\) et n sont des constantes positives. En l’absence de toute champ extérieur, la distance à l’équilibre est \(r_0\). L’énergie minimale à fournir pour dissocier cette molécule sera notée \(E_d\).

1. Interpréter physiquement les deux termes de l’énergie potentielle et représenter l’allure de \(E_p(r)\).

2. Interpréter graphiquement l’énergie \(E_d\) et déterminer son expression.

3. Repérer \(r_0\) sur le graphique et déterminer son expression. Vérifier que la position est stable.

4. En réalité, la molécule peut vibrer légèrement autour de sa position d’équilibre \(r_0\). Déterminer l’équation du mouvement et en déduire la pulsation \(\omega_0\) des petites oscillations. On introduira la constante de raideur équivalente \(k\).

5. Des mesures spectroscopiques permettent d’accéder expérimentalement à \(r_0, \omega_0\) et \(E_d\). Calculer les valeurs des constantes C, \(\alpha\) et n. On donne:

(9)\[\begin{align} &m = 1.66\times 10^{-27} \rm{kg}; e=1.6 \times 10^{-19} \rm{C}; r_0 = 1.27 \times 10^{-10} \rm{m};\\ &\omega_0 = 5.45 \times 10^{14} \rm{rad.s^{-1}}; E_d = 400 \rm{kJ.mol^{-1}} \end{align}\]

1. Le temps de réponse caractéristique de la molécule est \(\tau = 10^{-9} s\). Donner le facteur de qualité de cet oscillateur. Commenter cette valeur.

2. La molécule est maintenant excitée à sa fréquence propre par un champ électrique \(E(t) = E_0 \cos (\omega_0 t)\); nous supposons que la force subie alors par le noyau d’hydrogène est \(F(t) = \beta E(t)\) où \(\beta(t)\) est de l’ordre de l’unité. Déterminer l’amplitude des oscillations forcées.

3. Dans quel domaine de longueur d’onde faudrait-il travailler pour briser cette liaison en l’éclairant? Quelle marge possède-t-on sur le choix de la longueur d’onde?

4. Discuter la validité du modèle linéaire, et le choix de la longueur d’onde excitatrice.

Point utile pour cet exercice

• \(\Longrightarrow\) Système conservatif.

• \(\Longrightarrow\) Position d’équilibre et stabilité.

• \(\Longrightarrow\) Oscillateur harmonique.

• \(\Longrightarrow\) Oscillateur amorti.

• \(\Longrightarrow\) Oscillateur forcé.

Système de deux points matériels

Deux points matériels A et B de même masse m sont reliés entre eux par un ressort de raideur K et à deux points fixes par deux ressorts de raideur k. L’ensemble coulisse sans frottements sur une tige horizontale fixe. On note \(\overrightarrow{u}\) un vecteur unitaire de cet axe. On note x et y les élongations de A et B comptées à partir de leur position d’équilibre.

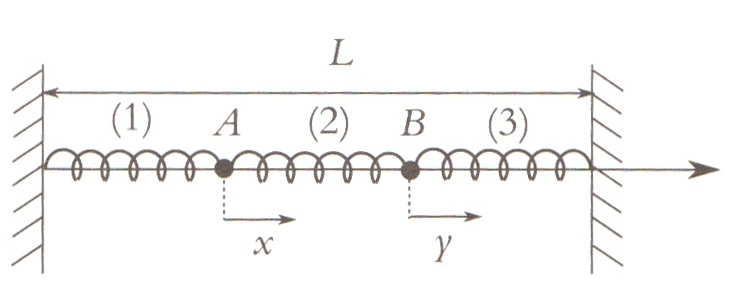
1. Ecrire les relations à l’équilibre reliant les longueurs à vide des ressorts (\(l_0\) pour (1) et (3), \(L_0\) pour (2)) et les longueurs à l’équilibre (\(l_{eq}\) pour (1) et (3), \(L_{eq}\) pour (2)).

2. Le point A subit une force supplémentaire \(\overrightarrow{f} = m \Gamma_0 \cos (\omega t)\overrightarrow{u}\). Déterminer les équations du mouvement. En déduire deux équations différentielles liées.

On cherche pour x et y, des solutions au régime sinusoïdal forcé de la forme \(x(t) = X_0 \cos (\omega t + \phi)\) et \(y(t) = Y_0 \cos (\omega t +\psi)\). On définit les grandeurs complexes associés \(\underline{X} = X_0 e^{j \omega t + \phi}\) et \(\underline{Y} = Y_0 e^{j \omega t + \psi}\). Montrer que les solutions des équations différentielles précédentes sont:

\[\begin{align*} \underline{X} &= \frac{\omega_0^2 - \omega^2}{(\omega_2^2 - \omega^2)(\omega_1^2 - \omega^2)} \Gamma_0 e^{j \omega t}\\ \underline{Y} &= \frac{\omega_3^2}{(\omega_2^2 - \omega^2)(\omega_1^2 - \omega^2)}\Gamma_0 e^{j \omega t} \end{align*}\]

où \(\omega_0, \omega_1, \omega_2, \omega_3\) sont des grandeurs à exprimer en fonction de k,K et m.

1. Déduire des expressions précédents \(X_0(\omega), Y_0(\omega), \phi(\omega)\) et \(\psi(\omega)\).

2. Représenter \(X_0(\omega), Y_0(\omega)\) en fonction de \(\omega\). Pourquoi y a-t-il des résonances infinies?

Point utile pour cet exercice

• \(\Longrightarrow\) Oscillateur forcé.

• \(\Longrightarrow\) Etude fréquentielle.