Entrainement : Cinématique du point

Vélodrome

Exercice

On s’intéresse à un cycliste, considéré comme un point matériel M, qui s’entraîne sur un vélodrome constitué de deux demi-cercles de rayon \(R= 20 \rm{cm}\) relié par deux lignes droites de longueurs \(L = 62 \rm{cm}\). Le cycliste part de D, milieu d’une ligne droite avec une vitesse nulle. Il exerce un effort constant qui se traduit par une accélération tangentielle au mouvement constante \(a_1\). On note \(C_1\) et \(C_2\) les centres des deux demi-cercles.

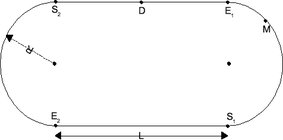
1. De D, le cycliste se dirige vers le point \(E_1\), entrée du demi-cercle. Justifier que l’accélération normale à la vitesse est nulle puis calculer le temps \(t_{E1}\) de passage en \(E_1\) ainsi que la vitesse \(v_{E1}\) en \(E_1\) en fonction de \(a_1\) et L.

2. On étudie le mouvement du cycliste dans le demi-cercle entre \(E_1\) et \(S_1\).

   1. Justifier l’utilisation d’une base cylindrique dont on précisera le centre. On prendra l’angle \(\theta\) par rapport à l’axe \(C_1 E_1\).

   2. Déterminer le temps que \(t_{S1}\) de passage en \(S_1\) en fonction de \(a_1\), \(L\) et \(R\) ainsi que la vitesse \(v_{S1}\) en \(S_1\).

   3. On note \(v(t)\) la vitesse du cycliste à chaque instant. Montrer que l’accélération normale au mouvement est non nulle dans le demi-cercle et qu’elle vaut à chaque instant \(a_N = \frac{{v(t)}^2}{R}\).

3. Calculer de même les temps de passage \(t_{E2}, t_{S2}, t_D\) respectivement en \(S_1, S_2,D\) (après un tour) ainsi que les vitesses \(v_{E1}, v_{E2}, v_D\).

4. La course se fait sur quatre tours et est longue de 1km mais on ne s’intéresse ici qu’au premier tour effectué en \(T_1=18,155 \rm{s}\) (par le britannique Chris Roy aux Championnats du monde de 2007).

5. Déterminer la valeur de l’accélération a1 ainsi que la vitesse atteinte en D. La vitesse mesurée sur piste est d’environ \(v_D = 60 \rm{km.h^{-1}}\). Que doit-on modifier dans le modèle pour se rapprocher de la réalité?

Eléménts de réponse (sans justification)

• \(t_{E1} = \sqrt{\frac{L}{a_1}}\) et \(v_{E1} = \sqrt{a_1 L}\).

• \(t_{S1} = \sqrt{\frac{L + \frac{\pi}{2}R}{a_1}}\) et \(v_{S1} = \sqrt{a_1 (L + \frac{\pi}{2}R)}\).

• \(t_{E2} = \sqrt{\frac{3L + \frac{\pi}{2}R}{a_1}}\) et \(v_{E2} = \sqrt{a_1 (3L + \frac{\pi}{2}R)}\).

• \(t_{S2} = \sqrt{\frac{3L + \pi R}{a_1}}\) et \(v_{S2} = \sqrt{a_1 (3L + \pi R)}\).

• \(t_{D} = \sqrt{\frac{4L + \pi R}{a_1}}\) et \(v_{D} = \sqrt{a_1 (4L + \pi R)}\).

Point utile pour cet exercice

• \(\Longrightarrow\) Base de Frenet

• \(\Longrightarrow\) Trajectoire circulaire.

• \(\Longrightarrow\) Vitesse et accélération en cylindrique.

Trajectoire d’un bateau

Exercice

On s’intéresse à une planète semblable à la Terre mais entièrement recouverte d’eau. On assimile la planète à une sphère de rayon R. Un bateau se déplace à la surface de cette planète, avec une vitesse constante \(V_0\) et toujours en direction du Nord-Est.

1. Exprimer les différentes composantes de la vitesse en projection dans la base de coordonnées sphériques associé au repère terrestre.

2. Déterminer par intégration des équations précédentes, les expressions de la colatitude \(\theta\) et de la longitude \(\phi\) en fonction du temps.

3. Quelle est la date d’arrivée au pôle?

Eléments de réponse (sans justification)

• \(\theta(t) = \theta_0 - \frac{\sqrt{2}}{2}\frac{V_0}{R}t\)

• \(\phi(t) = \ln \frac{\tan \theta_0 / 2}{\tan \frac{\theta_0 - \frac{\sqrt{2}V_0}{2R}t}{2}}\)

Point utile pour cet exercice

• \(\Longrightarrow\) Base sphérique.

• \(\Longrightarrow\) Vitesse en sphérique.

Poursuite

Exercice

Quatre robots repérés par les points A,B,C et D sont initialement aux sommets d’un carré de côté \(a\) et de centre O. Le robot A est programmé pour toujours se diriger vers B avec une vitesse de norme constante \(v\), de même B se dirige toujours vers C à vitesse v… . On s’intéresse au mouvement de A.

Déterminer alors les équations paramétriques du mouvement de A (équation horaire) en fonction de t et v puis l’instant \(t_0\) d’arrivée en O.

Eléments de réponse (sans justification)

• \(r(t) = \frac{\sqrt{2}}{2}a - \frac{\sqrt{2}}{2}v_0 t\)

• \(\theta(t) = - \ln \left ( a - v_0 t\right )\)

Point utile pour cet exercice

• \(\Longrightarrow\) Base cylindrique.

• \(\Longrightarrow\) Vitesse en cylindrique.

• \(\Longrightarrow\) Symétrie.