Entrainement

Saut à l’elastique

Dans tout le problème, on ne tient pas compte des frottements de l’air. Un fabricant de saut à l’élastique donne les caractéristiques suivant pour un type d’élastique:

• Type M: pour un poids de 65 à 95kg

• Longueur à vide (notée \(l_0\)): de 6m à 50m pour des sites de saut de 30m à 250m.

• Tension appliquée sur un élastique pour un allongement de \(100\%\): 200kg

• Tension appliquée sur un élastique pour un allongement de \(200\%\): 325kg

On prendra \(g = 9.8 \rm{m.s^{-2}}\).

1. Traduire la fiche technique en langage correct pour la physique.

2. La tension de l’élastique obéit-elle à une loi type ressort: \(T = k (l-l_0)\) où T est la tension appliquée et l la longueur de l’élastique?

3. On supposera dans la suite que la tension est de la forme \(T = k (l-l_0)\). A partir des données, déterminer une valeur moyenne de la constante de raideur de l’élastique k pour un élastique de \(l_0 = 6 \rm{m}\).

4. On veut savoir à quelle hauteur remonterait une masse test M de masse minimale (ici \(m=65\rm{kg}\)) si elle est lâchée sans vitesse initiale, l’élastique tendu au maximum. On prendra l’exemple d’un élastique de \(l_0 = 6 \rm{m}\), dont le point d’attache est à la hauteur \(h=18\rm{m}\) au dessus du point de départ.

   1. Déterminer l’expression de l’altitude \(z(t)\) et de la vitesse \(\dot z(t)\) tant que l’élastique est tendu.

   2. Calculer l’instant \(t_1\) pour lequel l’élastique n’est plus tendu. En déduire la vitesse de M à cet instant.

   3. Déterminer la hauteur maximale atteinte par l’objet.

5. On réalise maintenant un saut normal, à partir du point d’attache, sans vitesse initiales (le sauteur a les mêmes caractéristiques que la masse test et on utilise le même élastique).

   1. Déterminer le point le plus bas atteint par le sauteur et l’accélération ressentie en ce point.

   2. En réalité, les frottements de l’air entraîne l’immobilisation du sauteur après plusieurs oscillations. A quelle hauteur s’immobilise-t-il?

Point utile pour cet exercice

• \(\Longrightarrow\) Pesanteur.

• \(\Longrightarrow\) Action d’un ressort.

• \(\Longrightarrow\) PFD.

• \(\Longrightarrow\) Méthodes de résolution du PFD (ordre 2).

Eléments de réponse (sans justification)

Dans les deux cas l’origine est prise au niveau du point d’attache et l’axe Oz est orienté vers le haut.

Pour la masse test:

\[\begin{align*} z(t) &= - (\frac{mg}{k} + l_0) - \left(h - \frac{mg}{k} - l_0\right) \cos \omega_0 t &\textrm{ pour }t < t_1\\ z(t) &= -\frac{g}{2} {\left(t- t_1\right)}^2 + v_1 \left(t- t_1\right) - l_0 &\textrm{ pour }t > t_1 \end{align*}\]

avec \(\omega_0 = \sqrt{\frac{k}{m}}\), l’instant où l’élastique se détend \(t_1 = \frac{1}{\omega_0} \arccos \left ( - \frac{\frac{mg}{k}}{h - \frac{mg}{k}- l_0} \right )\) et la vitesse à cet instant vaut \(\dot z(t) = v_1 = \omega_0 \sqrt{\left ( h - \frac{2mg}{k}-l_0 \right )\left ( h - l_0\right)}\).

L’altitude maximale atteinte est alors: \(\frac{v_1^2}{2g} - l_0\)

Pour le saut normal:

\[\begin{align*} z(t) &= -\frac{g}{2}t^2 &\textrm{ pour }t < t_2\\ z(t) &= - (\frac{mg}{k} + l_0) + \frac{mg}{k}\cos \left(\omega_0 \left(t - t_2\right)\right) - \sqrt{2l_0 g} \sin \left(\omega_0 \left(t - t_2\right)\right) &\textrm{ pour }t > t_2\\ \end{align*}\]

avec \(\omega_0 = \sqrt{\frac{k}{m}}\), l’instant où l’élastique se tend \(t_2 = \sqrt{\frac{2l_0}{g}}\).

L’altitude minimale atteinte est alors: \(z_m = - \left ( \frac{mg}{k} + l_0 \right ) \left ( 1 + \sqrt{1 - {\left ( \frac{l_0}{\frac{mg}{k}+ l_0}\right )}^2}\right )\)

L’accélération subit vaut alors: \(a = \frac{k}{m}(z_m - l_0) - g\)

Immobilisation à \(z_e = -\frac{mg}{k} - l_0\)

Cascade en voiture

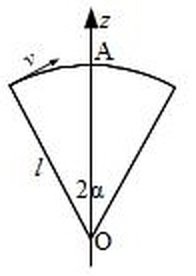
Une automobile, assimilée à un point matériel, circule à la vitesse v uniforme, sur une piste au profil accidenté. Elle franchit une bosse (cf. Figure)), modélisée par deux portions rectilignes raccordés par un arc de cercle de rayon \(l\), de centre O et d’ouverture angulaire \(2 \alpha\).

1. Faire un bilan sommaire des forces extérieures.

2. A quelle condition garde-t-elle contact avec le sol? A.N.: \(\alpha = 10 ^{\circ}; l = 5\rm{m}\). (on pourra considérer que le centre d’inertie touche le sol pour simplifier l’étude).

La voiture est maintenant assimilée à un point matériel de masse \(m=1000\rm{kg}\). On prend \(l=130\rm{m}\) et \(\alpha = 15 ^{\circ}\). La voiture est au sommet de la bosse (point noté A) avec une vitesse de \(v_0 = 125 \rm{km.h^{-1}}\) (on ne cherche pas à savoir comment elle est arrivée là). Sa vitesse n’est plus forcément constante.

On suppose que durant la descente, la composante “motrice” de l’action de contact avec le sol est de valeur algébrique \(F\) constante (positive pour une accélération, négative pour un freinage).

3. Déterminer une équation différentielle du mouvement de \(M(r, \theta)\)faisant intervenir la dérivé seconde de \(\theta\). On prendra l’origine des angles \(\theta\) suivant la verticale, c’est-à-dire suivant la direction OA.

4. Après avoir multiplié l’équation par \(\dot \theta\), l’intégrer.

5. Déterminer l’expression vérifiée par l’angle \(\theta_d\) pour lequel la voiture quitterait le sol.

6. Calculer cet angle dans le cas où le conducteur coupe le moteur en A (on prendra \(g = 9.8 \rm{m.s^{-2}}\)). Conclure.

7. Est-il préférable d’accélérer ou de freiner? Calculer la valeur de F pour que la voiture arrive à la fin de la bosse (fin de l’arc de cercle) sans encombre. Est-ce une valeur minimale ou maximale?

8. On reprendra cette étude par une application du théorème du moment cinétique.

Point utile pour cet exercice

• \(\Longrightarrow\) Pesanteur.

• \(\Longrightarrow\) PFD.

• \(\Longrightarrow\) Détermination d’une force.

• \(\Longrightarrow\) Condition de contact.

• \(\Longrightarrow\) Méthodes de résolution du PFD (multiplication par la dérivée première).

Eléments de réponse (sans justification)

Cas à vitesse constante: \( \alpha < \arccos \frac{v^2}{Rg}\)

Cas à force constante:

\[\begin{align*} -m R \dot \theta ^2 &= N - mg \cos \theta\\ m R \ddot \theta &= F + mg \sin \theta \end{align*}\]

\(- \frac{mv_0^2}{R}- 2F\theta_d + 3 mg \cos \theta_d = 0\)

Arrosage

Un tuyau demi-cylindrique de section négligeable est posé sur le sol. Sur une longueur \(l\), le demi-cylindre est percé d’un très grand nombre de petits trous régulièrement répartis. Il en sort des jets d’eau, tous perpendiculaires au tuyau d’arrosage selon tous les angles entre 0 et \(\pi\) à la même vitesse \(v_0\). Le débit total (masse d’eau dispersée par unité de temps) est \(D_m\). On suppose que chaque jets d’eau se comporte de manière indépendante et on néglige les frottements de l’air.

1. Déterminer la distance x de portée du jet d’eau pour un trou en fonction de l’angle \(\theta\) que fait le jet au départ du tuyau.

2. En déduire la longueur élémentaire \(dx\) arrosée par les jets sortis des trous situé entre les angles \(\theta\) et \(\theta + d \theta\) puis la surface dS arrosée par ces mêmes jets.

3. Déterminer le débit élémentaire dD sortant entre les angles \(\theta\) et \(\theta +d \theta\).

4. En déduire la densité d’arrosage d, c’est-à-dire la masse reçue par unité de temps et par unité d’air (on fera attention aux angles arrosant la même surface élémentaire).

Point utile pour cet exercice

• \(\Longrightarrow\) Pesanteur.

• \(\Longrightarrow\) PFD.

• \(\Longrightarrow\) Calcul différentiel.

Eléments de réponse (sans justification)

\(d = D_m \frac{g}{2v^2 \pi \cos 2 \theta}\)