Action ponctuelle: Modélisation et typologie

Introduction

Comme nous l’avons vu, l’action ponctuelle possède une grande importance car une action résultante est définie initialement comme un regroupement d’actions ponctuelles. Nous allons donc voir comment modéliser mathématiquement une action ponctuelle. Nous nous en servirons dans ce chapitre pour décrire des actions usuelles ponctuelles comme les interactions fondamentales (gravitation et électromagnétiques) ainsi que quelques actions dont la modélisation ponctuelle reste valable pour la grande majorité des systèmes d’étude.

Nous verrons dans le cas où le système est un point matériel comment on peut déterminer certaines caractéristiques des actions inconnues en statique ou prévoir l’évolution qualitative du mouvement en dynamique. Nous introduirons enfin le moment des forces qui aura, comme nous le verrons par la suite un effet sur la rotation du système et donc sur le moment cinétique du système.

Modélisation mathématique

Dans le cas d’un système constitué d’un unique point matériel M, le point d’application est nécessairement le point M (et les actions du milieu extérieur sont toutes nécessairement des actions ponctuelles).

Important

Modélisation d’une action ponctuelle

Soit une action ponctuelle \(\mathfrak{A}_{1 \to 2}\) d’un système \(\Sigma_1\) sur un système \(\Sigma_2\). On modélise mathématiquement cette action par deux caractéristiques:

• sa force \(\overrightarrow{F}(\mathfrak{A}_{1 \to 2})\) (noté souvent simplement \(\overrightarrow{F}\)) qui donne la direction et le sens vers laquelle l’action tend à entraîner le système et avec quelle intensité elle tend à entraîner le système.

• son point d’application.

Par principe physique, les caractéristiques d’une action sont indépendantes du référentiel considéré.

Attention

La force \(\overrightarrow{F}\) donne la direction et le sens vers laquelle l’action tend à entraîner le système mais cela ne veut pas dire que le sytème va aller dans sa direction. Son inertie peut lui permettre de continuer dans une autre direction. Il sera simplement dévié/ralenti (plus ou moins fortement suivant son inertie et l’intensité de la force).

Exemple: Un objet lancé vers le haut subit l’action de la pesanteur dirigée vers le bas mais il continue à monter (en étant par contre ralenti).

Moment d’une action

Définition

Par abus de langage (quasi systématique), on parle de moment d’une force et non de moment d’une action.

Important

Moment d’une action ponctuelle par rapport à un point.

Soit une action ponctuelle \(\mathfrak{A}_{1 \to 2}\) d’un système \(\Sigma_1\) sur un système \(\Sigma_2\) modélisée par une force \(\overrightarrow{F_{ext \to A}}\) et un point d’application A.

Soit un point B de l’espace. On définit le moment \(\overrightarrow{M_B}(\mathfrak{A}_{1 \to 2})\) de l’action \(\mathfrak{A}_{1 \to 2}\) par rapport au point B par:

\[ \overrightarrow{M_B}\left(\mathfrak{A}_{1 \to 2}\right) = \overrightarrow{BA} \wedge \overrightarrow{F_{ext \to A}} \]

Important

Moment d’une action ponctuelle/force par rapport à un axe.

Soit une action ponctuelle \(\mathfrak{A}_{1 \to 2}\) d’un système \(\Sigma_1\) sur un système \(\Sigma_2\) modélisée par une force \(\overrightarrow{F}\) et un point d’application A.

Soit un axe \(\Delta\) orienté par un vecteur unitaire \(\overrightarrow{u_{\Delta}}\). On définit le moment \(M_{\Delta}(\mathfrak{A}_{1 \to 2})\) de l’action \(\mathfrak{A}_{1 \to 2}\) par rapport à l’axe \(\Delta\) par:

\[ M_{\Delta}\left(\mathfrak{A}_{1 \to 2}\right) = \overrightarrow{u_{\Delta}} \cdot \overrightarrow{M_{B}}\left(\mathfrak{A}_{1 \to 2}\right) = \overrightarrow{u_{\Delta}} \cdot \left(\overrightarrow{BA} \wedge \overrightarrow{F}\right) \]

où B est un point de l’axe \(\Delta\).

Attention

Ne pas confondre moment d’une action et moment cinétique. Ils n’ont même pas la même unité.

Moment d’une action: Interprétation (en ligne)

Interprétation du moment d’une action par rapport à un axe.

Dans toute la suite on travaillera implicitement dans un référentiel \(\mathfrak{R}\).

Pour interprêter le moment d’une action par rapport à un axe orienté \(\Delta\), on va se placer dans un repère cylindrique d’axe \(\Delta\) centré en un point O de l’axe.

On considère un point matériel M subissant une action \(\mathfrak{A}\) modélisée par une force \(\overrightarrow{F}\) (appliquée donc au point M). On note l’expression de \(\overrightarrow{F} = F_r \overrightarrow{e_r} + F_{\theta} \overrightarrow{e_{\theta}} + F_z \overrightarrow{e_z}\).

On peut donc calculer le moment de l’action modélisée par \(\overrightarrow{F}\) sur \(\Delta\) (Le point A est le point d’application de l’action):

\[\begin{align*} M_{\Delta}(\mathfrak{A}) &= \overrightarrow{u_{\Delta}} \cdot \overrightarrow{M_O (\mathfrak{A})}\\ &= \overrightarrow{u_{\Delta}} \cdot \left( \overrightarrow{OA}\wedge \overrightarrow{F}\right)\\ &= \overrightarrow{e_z} \cdot ((r_A \overrightarrow{e_r} + z_A \overrightarrow{e_z}) \wedge (F_r \overrightarrow{e_r} + F_\theta \overrightarrow{e_{\theta}} + F_z \overrightarrow{e_z}))\\ &= r_A F_\theta \end{align*}\]

On observe que:

• Le moment de l’action \(\mathfrak{A}\) sur l’axe \(\Delta\) n’est pas nul si la composante orthoradiale \(F_{\theta}\) est non nulle. Or la composante orthoradiale correspond à la (seule) composante de \(\overrightarrow{F}\) qui tend à faire tourner le point M autour de l’axe \(\Delta\) (la composante suivant Oz tend à le faire longer l’axe Oz et la composante suivant \(\overrightarrow{e_r}\) ne fait qu’éloigner ou rapprocher le point M de l’axe.

Le moment d’une action sur un axe donne donc une information sur la possibilité que possède cette action (seule) à faire tourner le système autour de l’axe considéré..

• Il est algébrique et le moment de l’action est positif si \(F_{\theta} > 0\) c’est-à-dire si l’action tend à faire tourner le système suivant les \(\theta\) positifs (on généralisera en remarquant qu’il s’agit de faire tourner le système dans un sens en cohérence avec l’orientation de l’axe considéré). A l’inverse, si \(F_{\theta} < 0\), l’action tend à faire tourner le système en sens inverse.

Et si la composante orthoradiale est nulle, cela signifie que l’action n’a pas d’effet sur la rotation autour de l’axe. Elle ne fait qu’éloigner/rapprocher le système de l’axe ou le faire longer l’axe.

• On remarquera que le moment de l’action est aussi plus important quand r est grand. Si l’on fait le parallèle avec la force, on comprend que plus le moment est grand, plus il sera capable de modifier la rotation du système autour de l’axe considéré. Or on observe expérimentalement que plus l’action est loin de l’axe de rotation, plus elle a d’effet sur le système (principe du bras de levier utilisé par Archimède), il est donc normal que le moment de la force soit proportionnel à la distance r à l’axe.

Important

Interprétation

On retiendra que le moment d’une action sur un axe \(\Delta\) donne la tendance qu’à cette action à faire tourner le système autour de l’axe. Il donne par son signe le sens dans lequel cette tendance se fait.

Attention

• Il s’agit d’une tendance pour l’action considéré. (notion d’inertie)

• Cela ne veut pas dire que le système est en rotation autour de l’axe, il peut même être immobile (les considérations sur les moments sont très important en statique des systèmes de points).

  • Comme pour la force, le moment donne une tendance qui sera réalisée ou non suivant l’existence d’autres actions/contraintes et suivant l’inertie et le mouvement initial du système.

Actions ponctuelles usuelles

Nous allons présenter ici les actions usuelles dont les caractéristiques des forces doivent être connues. Il s’agit pour la plupart d’action ponctuelle s’exerçant sur des points matériels, il ne sera donc en général pas précisé le point d’application parce qu’il est alors évident.

On distingue les interactions à distance et les interactions de contact.

• Les premières regroupent des interactions fondamentales (gravitation et électromagnétisme) et des dérivées (pesanteur).

• Les secondes, représentent des actions résultant de multiples actions (principalement électrostatiques) à l’échelle microscopique. On parle aussi d’actions surfaciques puisque les actions microscopiques se font en surface. Il s’agit donc d’action globales mais dans certains cas, on peut les assimiler à des actions ponctuelles: quand le contact se fait sur une surface très petite (qu’on peut considérer à un point) ou quand on assimile le système à un point matériel.

Actions à distance

Force de Lorentz

Champ électromagnétique

Initialement, les champs électriques \(\overrightarrow{E}\) et magnétiques \(\overrightarrow{B}\) sont la conséquence de la présence de charges (pour le champ électrique) en mouvement (pour le champ magnétique) et vont agir sur d’autres particules chargées. On peut les voir comme des intermédiaires de calcul dont l’interaction électromagnétique entre deux systèmes chargées: on s’intéresse d’un côté aux charges qui crée le champ puis on s’intéresse à l’action du champ sur les particules dont on veut étudier le mouvement.

On peut donc “oublier” les éléments qui causent l’existence des champs électromagnétiques en posant leur existence et s’intéresser uniquement à leur action sur des particules chargés. Quand on continue en physique, on peut observer que les champs électromagnétiques ne sont pas que des “intermédiaires de calcul” mais possède leur réalité propre et leurs caractéristiques propres qui permet de les étudier indépendamment du reste (cf. deuxième année). On va ici simplement s’intéresser à l’action ponctuelle d’un champ électromagnétique sur une particule chargée (donc ponctuelle).

Important

Force de Lorentz

Soit un point matériel M chargé de charge q et un champ électromagnétique donc les expressions vectorielles au point M sont \(\overrightarrow{E}(M)\) et \(\overrightarrow{B}(M)\). Alors le champ électromagnétique exerce une action dont la force, appelée force de Lorentz s’écrit:

\[ \overrightarrow{F}_{Lorentz} = q \left(\overrightarrow{E}(M) + \overrightarrow{v_{M/\mathfrak{R}}} \wedge \overrightarrow{B}(M)\right) \]

où \(\overrightarrow{v_{M/\mathfrak{R}}}\) est la vitesse du point M dans le référentiel d’étude.

Forces newtoniennes

Forces newtoniennes

Les forces dites newtoniennes sont des interactions dont la force décroît en \(\frac{1}{r^2}\) où r est la distance entre les deux points matériels en interaction. On distingue deux interactions newtoniennes: les interactions coulombiennes entre deux particules chargées (elles correspondent à un cas particulier de la force de Lorentz) et les interactions gravitationnelles entre deux particules massiques.

Il s’agit de deux des 4 interactions fondamentales (les deux autres, l’interaction forte et l’interaction faible n’ont pas d’effet significatifs dans le cadre de la mécanique classique, elles ont un rôle à l’échelle du noyau).

On remarquera que l’interaction gavitationnelle est toujours attractive.

Important

Interactions gravitationnelles

Soit deux points matériels \(M_1\) et \(M_2\) de masses respectives \(m_1\) et \(m_2\). Les deux masses sont en interaction dites gravitationnelles. L’action de \(M_1\) sur \(M_2\) est modélisée par une force dirigée de \(M_2\) vers \(M_1\) dont l’expression est:

\[\begin{align*} \overrightarrow{F_{grav,1 \to 2}} &= - G m_1 m_2 \frac{\overrightarrow{M_1 M_2}}{M_1 M_2^3}\\ &= - \frac{G m_1 m_2}{r^2} \overrightarrow{u_{1 \to 2}} \end{align*}\]

où G est la constante de gravitation universelle dont l’expression est \(G = 6.67 \times 10^{-11} \rm{m^{3}.kg^{-1}.s^{-2}}\).

Dans la seconde expression, r est la distance \(M_1 M_2\) et \(\overrightarrow{u_{1 \to 2}}\) est le vecteur unitaire porté par la droite orientée de \(M_1\) vers \(M_2\).

Intérêt

Le champ de gravitation permet de séparer la cause (présence d’une masse) de la conséquence (action sur une autre masse). Cela devient très utile quand on travaille avec non plus des points mais des systèmes de points matériels qui créent le champ de gravitation. Ce dernier étant la somme (possiblement continue = intégrale !) des champ de gravitation créé par chaque points du système, on peut séparément calculer le champ de gravitation puis dans un second temps calculer l’action sur un système (un point - action ponctuelle ou un système de points - action résultante de l’ensemble des action gravitationnelle sur chaque point du système).

Important

Champ de gravitation

Soit un point \(M_1\) de masse \(m_1\). On dit que le point \(M_1\) créé dans tout point P de l’espace un champ de gravitation \(\overrightarrow{\mathfrak{G}_{M_1}}(P)\) dont l’expression est:

\[\begin{align*} \overrightarrow{\mathfrak{G}_{M_1}}(P) &= - G m_1 \frac{\overrightarrow{M_1 P}}{M_1 P^3} \end{align*}\]

Si l’on place en un point P un point matériel \(M_2\) de masse \(m_2\), alors le point \(M_2\) subira une action gravitationnelle de la part de \(M_1\): \(\overrightarrow{F_{grav,1 \to 2}} = m_2 \overrightarrow{\mathfrak{G}_{M_1}}(P = M_2)\).

On remarquera que l’interaction coulombienne peut être attractive si les charges sont opposées et répulsive si les charges sont de même signe.

Important

Interactions coulombiennes (ou électrostatiques)

Soit deux points matériels \(M_1\) et \(M_2\) chargés de charges respectives \(q_1\) et \(q_2\). Les deux charges sont en interaction dites coulombiennes. L’action de \(M_1\) sur \(M_2\) est modélisée par une force portée par la droite \(M_1 M_2\) dont l’expression est:

\[\begin{align*} \overrightarrow{F_{elec,1 \to 2}} &= \frac{q_1 q_2}{4 \pi \epsilon_0} \frac{\overrightarrow{M_1 M_2}}{M_1 M_2^3}\\ &= - \frac{q_1 q_2}{4\pi \epsilon_0 r^2} \overrightarrow{u_{1 \to 2}} \end{align*}\]

où \(\epsilon_0\) est la permittivité électrique du vide dont l’expression est \(\epsilon_0 = 8.85 \times 10^{-12} \rm{s^{4}.A^{2}.kg^{-1}.m^{-3}}\) soit \(\frac{1}{4 \pi \epsilon_0} = 8.99 10^{9} S.I.\).

Dans la seconde expression, r est la distance \(M_1 M_2\) et \(\overrightarrow{u_{1 \to 2}}\) est le vecteur unitaire porté par la droite orientée de \(M_1\) vers \(M_2\).

Intérêt

Le champ électrique permet, comme le champ de gravitation, de séparer la cause (présence d’une charge) de la conséquence (action sur une autre charge). Cela devient très utile quand on travaille avec non plus des points mais des systèmes de points matériels chargés qui créent le champ électrique. Ce dernier étant la somme (possiblement continue = intégrale !) des champs électrique créé par chaque points du système, on peut séparément calculer le champ électrique puis dans un second temps calculer l’action sur un système (un point - action ponctuelle ou un système de points - action résultante de l’ensemble des action gravitationnelle sur chaque point du système).

Comme cela a été évoqué dans précédemment, les champs (et notamment le champ électrique) peut être étudié pour lui-même sans tenir compte de la cause de ce champ électrique. C’est le cas des ondes électromagnétiques.

Important

Champ électrique

Soit un point \(M_1\) de charge \(q_1\). On dit que le point \(M_1\) créé dans tout point P de l’espace un champ électrique \(\overrightarrow{E_{M_1}}(P)\) dont l’expression est:

\[\begin{align*} \overrightarrow{E_{M_1}}(P) &= \frac{q_1}{4 \pi \epsilon_0} \frac{\overrightarrow{M_1 P}}{M_1 P^3} \end{align*}\]

Si l’on place en un point P un point matériel \(M_2\) de charge \(q_2\), alors le point \(M_2\) subira une action coulmbienne de la part de \(M_1\): \(\overrightarrow{F_{grav,1 \to 2}} = q_2 \overrightarrow{E_{M_1}}(P = M_2)\).

Pesanteur sur un point matériel

Important

Champ de pesanteur

A la surface de la Terre, tout corps massique est attiré vers “le bas” par une action appelée poids. Pour un point matériel M de masse m, la force qui s’applique s’écrit \(\overrightarrow{P} = m \overrightarrow{g}\) où \(\overrightarrow{g}\) est le champ de pesanteur au point M. Il est dirigé vers “le bas” (en réalité, il permet de définir la verticale (principe du fil à plomb)).

Gravitation et pesanteur

Le champ de pesanteur résulte de l’action gravitationnelle de la Terre sur le point M et de l’effet de rotation du référentiel terrestre (rotation de la Terre sur elle-même). Comme c’est l’action gravitationnelle qui prédomine au voisinage de la surface terrestre (cf. deuxième année), on confond souvent la pesanteur à la gravitation.

Actions de contact

Tension d’un fil

Important

Tension d’un fil ou d’une tige rigide.

La tension d’un fil ou d’une tige rigide est l’action qu’exerce un fil/une tige sur un système accroché au fil/à la tige (c’est une action de contact). Dans le cas d’un fil/une tige fin(e) dont la torsion n’a pas d’influence (ou qui ne se tord pas), on peut assimiler cette action à une action ponctuelle.

La force exercée par le fil/la tige n’a pas d’expression connue a priori mais on sait que dans le cas d’un fil, elle est alors nécessairement vers le fil et non vers le système accroché (un fil ne peut que tirer le système). Pour une tige, la force peut être dans les deux directions.

Important

Cas d’une fil/d’une tige parfaite Un fil/une tige parfaite est un fil/tige sans masse. Dans ce cas la tension exercée en chaque point du fil/tige sur l’autre partie du fil est la même en tout point du fil/tige est égale à la tension exercée à chaque extrémité du fil/tige sur les systèmes accrochée. De plus la tension du fil/tige est alors tangente au fil/tige.

Démonstration

La démonstration fait intervenir le principe fondamentale de la dynamique: \(\frac{\rm{d}\overrightarrow{p}}{\rm{dt}} = \sum \overrightarrow{F_{ext \to systeme}}\). Si l’on considère une portion de fil, les deux actions qui s’appliquent sur la portion de fil sont la tension de partie de fil à gauche et la tension de la partie du fil à droite. Comme le fil est sans masse, la quantité de mouvement est nulle, il vient donc que les deux tensions du fil sont opposées de même intensité. Par symétrie, il vient que les tensions seront tangentes au fil.

Pour les portions de fils aux extrémités, le même raisonnement conduit à dire que l’action des systèmes accrochés aux extrémités sur le fil sont modélisées par des forces égales entre elles et égales à la tension du fil en chaque point. Par principe des actions réciproques, l’action du fil sur les systèmes accrochés aux extrémités est modélisée par une force d’intensité égale à cette tension.

Action d’un ressort: Force de rappel élastique

Important

Action d’un ressort

Soit un système accroché à un ressort. En général, on considère le point d’accroche comme ponctuel et la force exercée par le ressort à son extrémité sur le système comme tangente au ressort. Si le ressort est de masse négligeable (cas usuel), alors la force exercée par le ressort sur un système accroché à son extrémité s’écrit si sa longueur est l:

\[ \overrightarrow{F_{ressort\to extremite}} = -k \left(l - l_0\right) \overrightarrow{u_{ext}} = - k \Delta l \overrightarrow{u_{ext}} \]

où \(l_0\) est la longueur à vide du ressort, k sa raideur et \(\overrightarrow{u_{ext}}\) un vecteur unitaire tangent à l’axe de ressort et dirigé vers l’extérieur du ressort.

\(\Delta l = l - l_0\) est appelé allongement du ressort.

Position au repos et position à vide

Il ne faut pas confondre la position au repos et la position à vide. En effet, la longueur du ressort au repos d’un système complet (ressort + système accroché au bout du ressort) n’est pas nécessairement la longueur à vide. On peut penser à un ressort vertical au bout duquel on a attaché une masse. Au repos, la longueur du ressort sera différente de la longueur à vide: le ressort sera étiré ou compressé suivant que la masse soit accrochée au dessus ou au dessous.

Analyse de l’expression

On remarquera que la longueur à vide est bien la longueur que possède le ressort au repos lorsqu’aucune action n’est exercée à ses extrémités (donc lorsqu’il n’exerce aucune action à ses extrémités.

La raideur donne une information sur la facilité qu’on peut avoir à tendre ou compresser le ressort: plus la raideur est grande, plus la force nécessaire pour étendre ou compresser le ressort devra être grande.

On parle de force de rappel. En effet, lorsque le ressort est comprimé, l’allongement est négatif et la force est dirigée vers l’extérieur: le ressort essaie de se détendre. Lorsque le ressort est étendu, l’allongement est positif et la force est dirigée vers l’intérieur: le ressort essaie de se contracter. Dans tous les cas, le système accroché tend à être rappelé vers la position à vide par le ressort.

Contact solide et contact fluide

Important

Composante tangentielle et composante normale

En un point de contact M entre le système et le solide/fluide (qu’on appellera \(\Sigma_{ext}\)), l’action ponctuelle (modélisée par la force \(\overrightarrow{F}(M)\)) peut-être décomposée en deux composantes:

• une composante normale à la surface de contact \(\overrightarrow{F_{\perp}}(M)\)

• une composante tangentielle à la surface de contact \(\overrightarrow{F_{//}}(M)\)

Interprétation des composantes.

La composante normale correspond à une “réaction de non interpénétration”, le système extérieur tend à pousser le système au point M. Cela peut-être une tendance légère (cas d’un système extérieur déformable) ou une contrainte forte (le mouvement du système étudié dans la direction normale au point de contact est alors nul). Au jouant sur la géométrie du contact dans le second cas, on arrive à créer des liaisons dont les mouvements possibles (degré de liberté) sont définies précisément (surface de contact cylindrique conduit à une rotation et une translation suivante un axe, surface de contact plan sur plan conduit à… un mouvement plan).

Il s’agit d’une vision simplifiée pour s’adapter au modèle du point matériel. Une vision globale sera présentée dans les systèmes de points.

La distinction faible/forte vitesse reste pour l’instant qualitative. Sans précision contraire, on supposera l’écoulement laminaire.

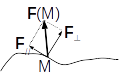
Important

Action d’un fluide L’action d’un fluide sur un point matériel est modéliée par une action de frottements fluides qui s’oppose à la vitesse. On distingue deux cas:

• Cas laminaire : Aux faibles vitesses, l’écoulement est dit laminaire et la force de frottement fluide est proportionnelle à la vitesse par rapport au fluide.

\[ \overrightarrow{f} = - \lambda \overrightarrow{v}_{M/fluide} \]

• Cas turbulent : Aux fortes vitesses, l’écoulement est dit turbulent et la force de frottement fluide est proportionnelle au carré de la vitesse par rapport au fluide.

\[ \overrightarrow{f} = - k \left \| \overrightarrow{v}_{M/fluide} \right \|\overrightarrow{v}_{M/fluide} \]

Important

Actions d’un solide : Lois phénoménologiques de Coulomb

En un point de contact solide-solide, la force de contact \(\overrightarrow{R}\) se décompose en deux composantes, l’une tangentielle \(\overrightarrow{R_T}\) et l’autre normale \(\overrightarrow{R_N}\) (\(\overrightarrow{R} = \overrightarrow{R_N} + \overrightarrow{R_T}\)). On déduit expérimentalement les comportements suivants:

• La composante normale est telle qu’elle empêche l’interpénétration des systèmes (contrainte cinématique). Elle est dirigée vers l’intérieur du solide qui subit l’action. Son annulaion signifie la perte de contact.

• La composante tangentielle a un comportement qui dépend de l’état relatif des deux solides:

  • en cas d’immobilité relative des deux solides, l’action complète est telle qu’elle permet l’immobilité relative. La composante tangentielle est de norme nécessairement limitée par l’inégalité

  \[ \left \| \overrightarrow{R_T}\right \| < \mu_S \left \| \overrightarrow{R_N}\right \| \]

  où \(\mu_S\) est appelé coefficient de frottement1 statique. Lorsque cette condition est mise en défaut, alors le système se met en mouvement.

  • en cas de mouvement relatif des deux solides (on dit qu’il y a glissement au point M), la composante tangentielle s’oppose à la vitesse relative au point M. Sa norme est égale à \(\left \| \overrightarrow{R_T}\right \| = \mu_D \left \| \overrightarrow{R_N}\right \|\) où \(\mu_D\) est appelé coefficient de frottement dynamique.

• Quelque soit le système, \(\mu_D < \mu_S\), c’est-à-dire qu’il est plus facile de maintenir un solide en mouvement par rapport à un autre solide malgré les frottements que de mettre en mouvement le même solide.

Attention

Il faut faire attention à plusieurs points:

• la condition d’immobilité est une inéquation. Elle ne permet PAS de déterminer la force ou le moment de l’action. Ces derniers se détermine par application des théorèmes fondamentaux dans un cas statique (immobilité relative des deux solides).

• Dans tous les cas, la composante normale se déduit de la contrainte cinématique imposée.

• La condition de contact est importante pour déterminer s’il y a décollement.

• Il faut faire attention à l’orientation de la composante tangentielle qui change en fonction de la vitesse uniquement lorsqu’il y a glissement. Cela signifie

  • qu’on doit souvent faire l’étude du mouvement par phase en fonction du sens de déplacement.

  • que dans le cas de non glissement, on ne peut a priori orienter la composante tangentielle.

---

1

Le terme de “frottement” statique est trompeur car du point de vue du sens commun, ça ne frotte pas !