Etude du mouvement

Position du problème

Position du problème On considère deux point matériel \(M_1\) et \(M_2\) de masses respectives \(m_1\) et \(m_2\) formant un système isolé (problème à deux corps) et dont l’interaction est de type newtonienne. Ainsi la force exercée par \(M_1\) sur \(M_2\) est de la forme: \(\overrightarrow{F} = - \frac{K}{r^2} \overrightarrow{e_r}\) où \(r\) est la distance entre les deux corps et \(\overrightarrow{e_r}\) le vecteur unitaire porté par la droite \((M_1 M_2)\) et dirigé de \(M_1\) vers \(M_2\).

Type d’approche

On peut considérer deux types d’approches:

• L’un des deux points matériels est nettement plus lourd (on suppose ici \(m_1 >> m_2\)). On admet qu’on peut alors se ramener à l’étude d’un seul corps, le point matériel \(M_2\) dans le référentiel \(R_1\) lié à \(M_1\). Le système étant isolé, on peut considérer que le référentiel \(R_1\) est galiléen. La résultante des forces qui s’exerce sur \(M_2\) est alors toujours dirigée vers le point \(M_1\): c’est un mouvement à force centrale. (Exemple: Interaction Terre-Soleil ou Proton-électron)

• Dans le cas général, il s’agit d’un système de deux points matériel. On admet qu’une étude complète des systèmes de deux points (HP) permettrait de se ramener au mouvement d’un point (fictif) soumis à une force centrale newtonienne.

On se ramène donc à étudier le mouvement d’un point matériel M soumis à une force centrale dans un référentiel galiléen.

On rappelle que dans un mouvement à force centrale, le moment cinétique est conservé. Ici la force est de plus conservative donc l’énergie mécanique est aussi une intégrale première du mouvement.

On va donc choisir un système de coordonnées cylindriques d’axe Oz colinéaire au moment cinétique. On va alors noter:

• Moment cinétique au point O: \(\overrightarrow{L_O} = m r^2 \dot \theta \overrightarrow{u_z} = m C \overrightarrow{u_z}\) où C est la constante des aires du mouvement.

• Force: \(\overrightarrow{F} = - \frac{K}{r^2} \overrightarrow{u_r}\)

• Energie potentielle: \(E_p = - \frac{K}{r}\)

• Energie mécanique: \(E_m = \frac{1}{2} m \dot r^2 + \frac{1}{2}\frac{mC^2}{r^2} - \frac{K}{r}\)

• Energie potentielle effective: \(E_{p,eff} = \frac{1}{2}\frac{mC^2}{r^2} - \frac{K}{r}\) \end{rappel}

Trajectoire

Trajectoire conique

Important

Trajectoire conique

Un point matériel M soumis à une force centrale newtonienne de type \(\overrightarrow{F} = - \frac{K}{r^2} \overrightarrow{e_r}\) dans un référentiel galiléen possède une trajectoire conique dont l’équation, dans un repère cylindrique d’axe Oz colinéaire au moment cinétique et de centre O le centre de force est:

\[ r(\theta) = \frac{p}{\epsilon + e \cos (\theta - \theta_0)} \]

où \(\epsilon= \pm 1\) et \(e\) est appelée excentricité et \(p\) le paramètre de la conique. On a: \(\vert p \vert = \frac{mC^2}{\vert K \vert}\)

On distingue les cas:

• une ellipse: \(e<1\) C’est un trajectoire fermée donc un état lié.

• une hyperbole: \(e>1\) C’est une trajectoire ouverte donc un état de diffusion.

• une parabole: \(e=1\) Cas limite entre les deux, c’est une trajectoire ouverte, donc un état de diffusion.

Trajectoire - Démonstration (en ligne)

Il existe plusieurs méthodes pour montrer que l’équation de la trajectoire est une conique. Le principe général est d’éliminer la variable temps dans les équations.

Démonstration

Le système est conservatif, donc l’énergie mécanique se conserve, soit: \(\frac{dE_m}{dt} = 0\). Nous allons introduire la coordonnées \(u = \frac{1}{r}\) et éliminer le temps en utilisant la constante des aires \(C = r^2 \dot \theta\).

Remarquons que:

\[\begin{align*} \frac{dr}{dt} &= \frac{dr}{d \theta} \frac{d \theta}{dt}\\ &= \frac{d (1/u)}{d \theta} \frac{C}{r^2}\\ &= - \frac{1}{u^2} \frac{du}{d \theta} C u^2\\ &= - C \frac{du}{d \theta} \end{align*}\]

On peut donc réexprimer l’énergie mécanique:

\[\begin{align*} \frac{1}{2} mC^2 (2 C u^2 \frac{du}{d \theta} \frac{d^2u}{d \theta^2} + 2 u Cu^2 \frac{du}{d \theta} - \frac{2K}{mC^2} Cu^2\frac{du}{d \theta}) &= 0\\ \frac{d^2u}{d \theta^2} + u &= \frac{K}{mC^2}\\ \end{align*}\]

On a écarté le cas \(u=0\) (physiquement impossible) et \(\frac{du}{d \theta} =0\) qui correspond à un mouvement circulaire. Comme on le verra par la suite, est inclus dans l’équation ci-dessus aussi.

On reconnaît une équation harmonique, donc:

\[\begin{align*} u(\theta) &= A \cos (\theta - \theta_0) + \frac{K}{mC^2}\\ r(\theta) &= \frac{\frac{mC^2}{K}}{1+ \frac{mC^2 A}{K} \cos (\theta - \theta_0)} \end{align*}\]

Trajectoire et énergie mécanique

Etude qualitative du mouvement

Dans le cas de l’hyperbole, seule une des deux branches est parcourue suivant que la trajectoire soit attractive (branche qui s’enroule autour du centre de force) ou répulsive (branche qui évite le centre de force).

Important

Energie potentielle effective.

On rappelle l’allure de l’énegie potentielle effective dans le cas attractif (premier) et répulsif (second). On rappelle que l’origine des potentiels a été choisi à l’infini.

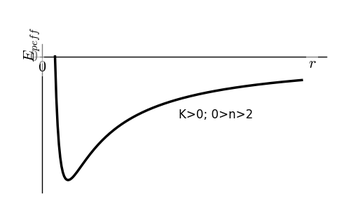
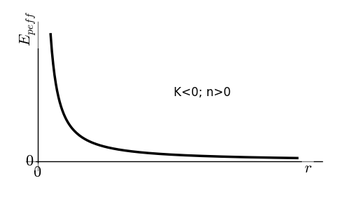
• Remarquons d’abord que dans le cas répulsif, la trajectoire est toujours de diffusion. Nous montrerons par la suite qu’il s’agit d’une hyperbole.

• Dans le cas attractif, il apparaît qu’un état lié correspond que l’énergie mécanique soit négative. La seule conique correspondant à un état lié est l’ellipse. Il vient qu’une énergie mécanique négative correspond à une trajectoire elliptique.

Si l’énergie mécanique est positive ou nulle, le système sera en état de diffusion soit une parabole ou une hyperbole. La distinction justifée par la suite entre les deux sera faite par la suite: le cas parabolique correspond au cas limite \(E_m = 0\) et le cas hyperbolique à \(E_m > 0\).

Important

Caractéristiques des trajectoires. Cas elliptique.

On prend \(\theta_0 = 0\).

• Cas attractif \(K > 0\)

• \(E_m < 0\)

• e < 1

• C’est un état lié donc périodique.

• Point le plus éloigné (aphélie pour les planètes autour du soleil): \(r_P = \frac{p}{1 - e}\) atteinte pour \(\theta = \pi\).

• Point le plus proche (périhélie pour les planètes autour du soleil): \(r_A = \frac{p}{1 + e}\) atteinte pour \(\theta = 0\)

• Toutes les valeurs de \(\theta\) sont possibles.

Important

Caractéristiques des trajectoires. Cas parabolique.

On prend \(\theta_0 = 0\).

• Cas attractif \(K > 0\)

• \(E_m = 0\)

• e = 1

• C’est un état de diffusion. A l’infini, la vitesse est nulle.

• Point le plus proche (périhélie pour les planètes autour du soleil): \(r_A = \frac{p}{1 + e} = \frac{p}{2}\) atteinte pour \(\theta = 0\)

• Toutes les valeurs de \(\theta\) sont possibles sauf \(\theta = \pi\)

Important

Caractéristiques des trajectoires. Cas hyperbolique

On prend \(\theta_0 = 0\).

Cas attractif

• Cas attractif \(K > 0\) et \(\epsilon = 1\)

• \(E_m > 0\)

• e > 1

• C’est un état de diffusion. A l’infini, la vitesse est non nulle.

• Point le plus proche (périhélie pour les planètes autour du soleil): \(r_A = \frac{p}{1 + e}\) atteinte pour \(\theta = 0\)

• Les valeurs de \(\theta\) sont comprises entre \(- \arccos \theta\) et \(\arccos \theta\).

Cas répulsif

• Cas répulsif \(K < 0\) et \(\epsilon = -1\)

• \(E_m > 0\)

• e > 1

• C’est un état de diffusion. A l’infini, la vitesse est non nulle.

• Point le plus proche (périhélie pour les planètes autour du soleil): \(r_A = \frac{p}{e - 1}\) atteinte pour \(\theta = 0\)

• Les valeurs de \(\theta\) sont comprises entre \(- \arccos \theta\) et \(\arccos \theta\).