Activités d’application¶
Cet exercice d’application directe est à faire à la suite du cours pour vérifier votre compréhension des méthodes. Vous pourrez confronter votre travail avec celui de vos camarades et poser des questions sur cet exercice en classe mais il ne sera pas donné de correction complète.
Energétique¶
Exercice
On appelle résistance 1/4W, une résistance pouvant dissiper au maximum une puissance P=0.25W. Déterminer, en fonction de R et P la tension maximale qu’on peut mettre à ses bornes et estimer la gamme de valeur de tension pour des résistances usuelles.
Etude d’une source réelle¶
Exercice
On considère une source réelle modélisable soit par un modèle de Thévenin de fem E et de résistance interne \(R_1\), soit par une source idéale de courant \(\eta\) en parallèle d’une résistance \(R_2\). Montrer qu’on doit avoir \(R_1 = R_2\) et \(E = R_1 \eta\).
On considère une source réelle modélisable soit par un modèle de Thévenin de fem E et de résistance interne \(R\). Montrer que la puissance maximale que peut délivrer la source est \(\frac{E^2}{4R}\)
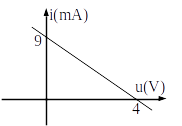
On considère un dipôle D dont la caractéristique est donnée ci-dessous. Déterminer les caractéristiques de sa modélisation de Thévenin.
Résistances équivalentes¶
Exercice
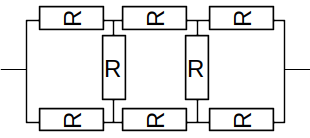
On considère le réseau de résistances suivantes. Déterminer la résistance équivalente en déterminant la relation u(i).
Correction
Réponses (sans justification)
\(R_e = \frac{3}{2} R\)
Exercice
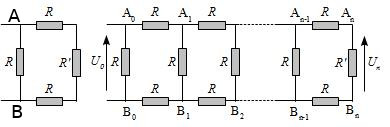
Déterminer R’ pour que la résistance équivalente entre A et B soit égale à R’ du premier circuit ci-dessus.
En déduire la valeur de \(U_{n+1}\) dans le second circuit ci-dessus si R’ a la valeur déterminée à la question précédente.
Quelle est la valeur de la résistance équivalente entre \(A_0\) et \(B_0\) dans le second circuit?
Correction
Réponses (sans justification)
\(R' = \left ( \sqrt{3} - 1\right )R\)
\(U_{n+1} = {\left ( \frac{\sqrt{3} - 1}{\sqrt{3} + 1}\right )}^{n+1} U_0\)
\(R'\)
Mise en équation¶
Exercice
Reprendre le montage du pont de Wheatstone et retrouver la tension \(U_{AB}\) en utilisant la loi des noeuds en terme de potentiel.
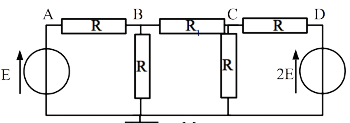
Reprendre le circuit ci-dessous et retrouver l’intensité i en utilisant les lois de Kirchhoff.
Exercice
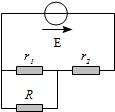
Exprimer le rendement \(\eta\) du diviseur de tension représenté sur le circuit ci-dessous (le rapport de la puissance dissipée dans la résistance de charge R à la puissance fournie par la tension E) en fonction de \(r_1, r_2\) et \(R\)
Correction
Réponse (sans justification)