Cas passe-bande¶
Exercice
On considère le circuit RLC série. Déterminer l’expression de la représentation complexe \(\underline{i}\) de l’intensité circulant dans le circuit.
Déterminer par une étude haute et basse fréquence la forme canonique compatible puis mettre \(\underline{i}\) sous cette forme. On déterminera la pulsation \(\omega_0\) et le facteur de qualité Q.
En déduire l’expression de l’amplitude réelle et du déphasage entre \(i\) et e en fonction de \(Q, \omega_0, R\) et \(e_m\).
Montrer que l’amplitude réelle passe par un extremum. On parle de résonance. Déterminer alors la pulsation de résonance, c’est-à-dire la pulsation pour laquelle l’amplitude réelle est maximale ainsi que l’amplitude maximale \(i_{\max}\).
Déterminer la bande passante, c’est-à-dire la gamme de fréquence/pulsation pour laquelle l’amplitude réelle est supérieure à \(\frac{i_{\max}}{\sqrt{2}}\). On calculera aussi la largeur de la bande passante.
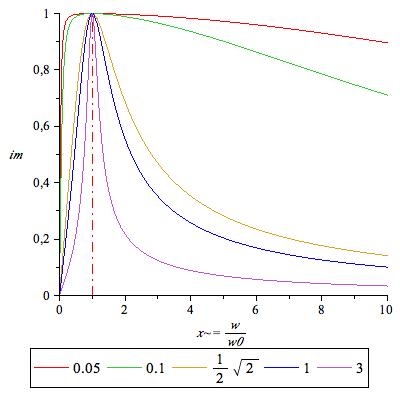
Représenter l’amplitude réelle en fonction de la fréquence pour différentes valeurs de Q.
Déterminer les valeurs du déphasage à haute et basse fréquence et représentation le daphasage en fonction de la fréquence.
Bilan : A retenir
On retiendra:
les caractéristiques hautes et basses fréquences nécessaires et la forme canonique associées lorsque le système est d’ordre 2.
la forme générale de la réponse fréquentielle (allure en fonction de la fréquence) en amplitude réelle et en déphasage.
l’existence d’une résonance, c’est-à-dire d’un maximum d’amplitude en fonction de la fréquence/pulsation dont la pulsation de résonance est toujours \(\omega_0\).
La largeur de la bande passante est \(\Delta \omega = \frac{\omega_0}{Q}\).