Dipôles linéaires actifs

Sources idéales

Source: dipôle polarisé

Les sources sont des dipôles polarisés. Il est important de préciser le sens dans lequel est orienté la f.e.m. ou le c.e.m.

Important

Source idéale de tension

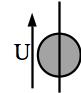
Fig. 13 Schéma d’une source idéale de tension

Une source idéale de tension est un dipôle dont la tension est une caractéristique propre du dipôle et ne varie pas, quelque soit l’intensité qui la traverse.

On appelle la tension à ses bornes force électromotrive (f.e.m.)

Important

Source idéale de courant

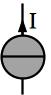
Fig. 14 Schéma d’une source idéale de courant

Une source idéale de courant est un dipôle dont l’intensité est une caractéristique propre du dipôle et ne varie pas, quelque soit la tensionà ses bornes.

On appelle l’intensité qui la traverse courant électromoteur (c.e.m.)

Caractéristique statique

• La caractéristique statique d’une source idéale de tension de fem E est une droite verticale d’équation u = E

• La caractéristique statique d’une source idéale de courant de cem I est une droite horizontale d’équation i = I

Source réelle: Electromoteur

Comportement réels des sources

En pratique, une source de tension ne délivre la fem voulue E qu’à vide, c’est-à-dire quand aucun courant ne sort. Lorsqu’on commence à demander une intensité en sortie (donc de la puissance), la fem u tend à diminuer. Expérimentalement, on observe qu’on peut modéliser cette chute par un modèle linéaire: \(u = E - Ri\). C’est le modèle des électromoteurs.

Important

Electromoteur

Un électromoteur linéaire est une modélisation d’une source donc la relation tension-intensité est:

\[ u = E - Ri \]

où E est la fem (à vide) de l’électromoteur et R sa résistance interne.

C’est une modélisation

Le modèle est Thévenin est comme son nom l’indique une modélisation, c’est-à-dire qu’elle permet d’étudier mathématiquement le comportement de la source réelle mais ne traduit pas la composition physique de la source (qui est bien plus complexe).

Important

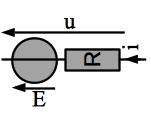
Modélisation de Thévenin d’un électromoteur

Un électromoteur peut être modélisé par une source idéale de tension de fem E en série avec une résistance R

Démonstration

Comme à chaque fois pour prouver/déterminer l’équivalence de deux dipôles, nous allons exprimer la relation intensité tension. Dans le cas de l’électromoteur, on a déjà \(u = E - Ri\)

La tension aux bornes du modèle proposé est (la résistance est orientée en convention générateur): \(u = E + u_R = E - R i\)

On a bien identification des équations d’évolution, donc l’électromoteur est modélisable par le modèle de Thévenin.