Entrainement : Filtrage linéaire#

Pulsation de coupure d’un filtre d’ordre 2

On considère un filtre passe-bas d’ordre 2 dont le facteur de qualité est \(Q = 1/2\).

  1. Montrer que le gain réel est strictement décroissant. Que vaut le gain réel maximal ?

  2. Déterminer la pulsation de coupure du filtre et montrer que \(\omega_c = \omega_0 \sqrt{-1 + \sqrt{2}}\).

  3. Reprendre le même exercice avec \(Q = 1 / \sqrt{2}\).

Etude fréquentielle

Pour chaque filtre ci-dessous, déterminer rapidement son type puis par le calcul sa fonction de transfert. On introduira la pulsation propre et si nécessaire le facteur de qualité et l’on précisera les asymptotes haute et basse fréquence sur le diagramme de Bode.

Pour les filtre d’ordre 1, on déterminera de plus la monotonie et la pulsation de coupure.

Pour les filtres d’ordre 2 passe-haut et bas, on déterminera l’existence possible d’une résonance ainsi que la pulsation de résonance. On déterminera aussi les valeurs particulières de la phase.

Pour les filtres passe-bande et coupe-bande, on déterminera la bande passante (ou la bande coupée) et on montrera que le produit des pulsations de coupure vaut la pulsation propre au carré.

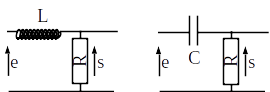
../_images/td_elec_phaut_bas_1.png
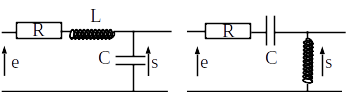
../_images/td_elec_phaut_bas_2.png
../_images/Electronique_TD4_EX1_1.jpg
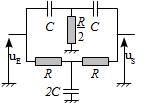
../_images/Electronique_TD4_EX1_2.jpg

Eléments de réponse (sans justification)

Dans l’ordre:

  • Passe-bas d’ordre 1. \(H_0 = 1\), \(\omega_0 = \frac{R}{L}\)

  • Passe-haut d’ordre 1. \(H_0 = 1\), \(\omega_0 = \frac{1}{RC}\)

  • Passe-bas d’ordre 2. \(H_0 = 1\), \(\omega_0 = \frac{1}{\sqrt{LC}}\) et \(Q = \frac{1}{R}\sqrt{\frac{L}{C}}\).

  • Passe-haut d’ordre 2. \(H_0 = 1\), \(\omega_0 = \frac{1}{\sqrt{LC}}\) et \(Q = \frac{1}{R}\sqrt{\frac{L}{C}}\).

  • Passe-bande d’ordre 2. \(H_0 = \frac{L_2}{L_1 + L_2}\), \(\omega_0 = \frac{1}{\sqrt{(L_1 + L_2)C}}\) et \(Q = R\sqrt{\frac{C}{L_1 + L_2}}\).

  • Coupe-bande d’ordre 2. \(H_0 = 1\), \(\omega_0 = \frac{1}{RC}\) et \(Q = \frac{1}{4}\).

Intégrateur pur

Cet exercice traite un montage que vous DEVEZ reconnaître et savoir étudier comme une question de cours.

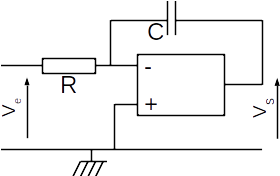
  1. Déterminer la relation entrée sortie du montage suivant en grandeur complexe puis la relation temporelle entrée-sortie. Justifier ainsi l’appelation du montage.

  2. Proposer une utilisation pratique de ce montage en sortie d’un capteur qu’on précisera. Quel problème ce montage risque-t-il de poser à basse fréquence ?

  3. Déterminer l’impédance d’entrée du montage.

../_images/elec_integrateur.png

Réponse d’un filtre d’ordre 1

On considère le filtre ci-après. On prend \(R=R_1=50 \rm{\Omega}\) et \(L = 10 \rm{mH}\)

  1. Déterminer le type de filtre puis la fonction de transfert.

  2. Donner une expression approchée (réfléchir au type de réponse approché le plus approprié) de \(u_{S}(t)\) pour: \begin{enumerate}1. un signal d’entrée sinusoïdal de fréquence 10kHz et d’amplitude 1V.

  3. un signal d’entrée sinusoïdal de fréquence 100Hz et d’amplitude 1V.

  4. un signal d’entrée créneau de période T=0,1ms.

  5. Représenter graphiquement \(u_E(t)\) et \(u_S(t)\) pour les trois signaux précédents et le comparer aux réponses exactes (on pourra utiliser une calculatrice graphique ou un simulateur). Commenter.

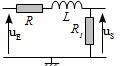
../_images/Electronique_TD4_EX3_1.jpg

Eléments de réponse (sans justification)

  • Passe-bas d’orrdre 1 avec \(H_0 = \frac{R_1}{R + R_1}\) et \(\omega_0 = \frac{R_1 + R}{L}\).

  • Dans l’ordre le premier signal de sortie est quasi-nul, le second non nul d’amplitude égale à l’entrée et en phase avec l’entrée et le troisième proche d’un sinusoïde.

Note: En pratique, les simulation montre que ce n’est pas tout à fait vrai car à l’ordre 1, l’assimilation à un filtre idéal n’est pas tout à fait correct.

Réponse d’un filtre d’ordre 2

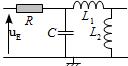
On place une bobine \(L_1\) et un condensateur \(C_1\) dans le circuit collecteur d’un transistor à effet de champ de façon à réaliser un amplificateur sélectif. Le montage ainsi obtenu est équivalent à celui ci-après. On a: \(\underline{I_0} = s \underline{v_e}\). \(s\) étant supposé constant et réel pour le domaine de fréquence étudié.

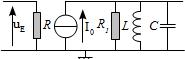
../_images/Electronique_TD4_EX4_1.jpg

  1. Déterminer la fonction de transfert \(\underline{H}\) sous la forme: \(\underline{H} = \frac{A_0}{1+ jQ (x - \frac{1}{x})}\) en notant \(x=\frac{\omega}{\omega_0}\). Quelle est la nature de ce filtre? Quelle est sa bande passante?

On envoie en entrée un signal périodique de pulsation \(\omega=\omega_0\). On définit le taux d’harmonique de rang n d’un signal périodique par le rapport \(\tau_{n} = \frac{V_n}{V_1}\) de l’amplitude \(V_n\) de l’harmonique de rang n à l’amplitude \(V_1\) du fondamental. On note \(\tau_{n,s}\) et \(\tau_{n,e}\) les taux d’harmoniques respectifs des signaux d’entrée et de sortie.

  1. Calculer le taux d’atténuation \(\delta_n = \frac{\tau_{n,s}}{\tau_{n,e}}\) de l’harmonique de rang n en fonction de Q et de n.

  2. On choisit alors la valeur de Q pour laquelle le taux d’atténuation est de -40dB pour l’harmonique de rang 2. Quelle valeur de Q réalise cette condition?

On envoie un signal créneau d’amplitude variant entre \(E_1\) et \(E_2\) de pulsation \(\omega_0\) en entrée. Celui-ci peut se décomposer en séries de Fourier (\(T_0 = \frac{2 \pi}{\omega_0}\) est la période du créneau):

\[ e(t) = \frac{E_1+E_2}{2} + \sum\limits_{p=0}^{+\infty}\frac{2(E_1-E_2)}{(2p+1) \pi} \sin((2p+1) \frac{2 \pi}{T_0} t) \]

  1. Représenter sur un graphique [fréquence;amplitude], le diagramme du signal puis donner l’allure du signal temporelle de sortie en le justifiant.

Eléments de réponse (sans justification)

  • \(A_0 = R_1 s\), \(\omega_0 = \frac{1}{\sqrt{LC}}\) et \(Q = R\sqrt{\frac{C}{L}}\)

  • \(\delta_n = \frac{1}{\sqrt{1 + Q^2 (n - \frac{1}{n})^2}}\)

  • Q = 67

  • Le signal de sortie pour le créneau sera un sinusoïde presque parfait.

Note: L’ordre 2 permet, à la différence de l’ordre 1 d’approcher le résultat approché de manière relativement bonne. Le problème est la réalisation d’un circuit avec un aussi grand facteur de qualité. Pour contourner le problème, il faudrait utiliser un filtre d’ordre supérieur.