Méthodes : Etudier un circuit en RSF

Etude d’un circuit RLC série

Nous allons voir ici comment utiliser directement les représentations complexes sur un circuit.

Exercice

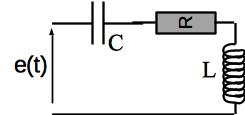
On considère un dipôle RLC série relié à une source idéale de tension délivrant une tension \(e(t) = e_m \cos \omega t\). Déterminer la tension aux bornes du condensateur et l’intensité traversant le dipôle en régime sinuoïdal forcé.

Correction

Méthode 1: Utilisation des lois de Kirchoff
La lois des mailles s’écrit: \(u_R + u_L + u_C = e\) et reste vraie avec les représentations complexes.
En régime sinusoïdal forcé, on utilise les impédances: \(\underline{u_R} = R \underline{i}; \underline{u_L} = j L \omega \underline{i}; \underline{u_C} = \frac{\underline{i}}{jC \omega}\). Il vient:

(49)\[\begin{equation} \left(R + j L \omega + \frac{1}{j C \omega}\right) \underline{i} = \underline{e} \Longrightarrow \underline{i} = \frac{\underline{e}}{R + j L \omega + \frac{1}{j C \omega}} \end{equation}\]

On déduite la tension \(u_C\):

(50)\[\begin{equation} \underline{u_C} = \frac{\underline{i}}{jC \omega} = \frac{\underline{e}}{jRC \omega - LC \omega^2 + 1} \end{equation}\]

Méthode 2: Pont diviseur
R, L et C forment un pont diviseur de tension, il vient que:

\[\begin{align*} \underline{u_C} = \frac{\underline{Z_C}}{\underline{Z_R} + \underline{Z_L} + \underline{Z_C}} \underline{e} = \frac{\underline{e}}{jRC \omega - LC \omega^2 + 1}\\ \underline{i} = \frac{1}{\underline{Z_R} + \underline{Z_L} + \underline{Z_C}} \underline{e} = \frac{\underline{e}}{R + j L \omega + \frac{1}{j C \omega}} \end{align*}\]

Passage aux grandeurs réelles
On ne va travailler ici que sur l’intensité.

Vérification du résultat.

En régime sinusoïdal forcé, on peut remarquer que \(C \omega\) est homogène à l’inverse d’une résistance et que \(L \omega\) est homogène à une résistance. Vous pouvez vérifier aisément que les grandeurs calculées sont homogènes (on rappelle qu’une phase est sans dimension).

D’autres vérification seront possibles lorsque nous aurons étudié les comportements asymptotiques.

Amplitude réelle:

(51)\[\begin{equation} i_m = \left\vert \underline{i} \right\vert = \frac{e_m}{\sqrt{R^2 + {\left(L \omega - \frac{1}{C \omega}\right)}^2}} \end{equation}\]

Phase à l’origine:

(52)\[\begin{equation} \phi_i = \arg \underline{i} = \arg \underline{e} - \arg \left(R + j \left(L \omega - \frac{1}{C \omega}\right)\right) = - \arctan \frac{1}{R}\left(L \omega - \frac{1}{C \omega}\right) \end{equation}\]

Utilisation de la loi des noeuds en terme de potentiel

Exercice

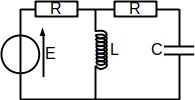
On considère le circuit ci-dessous où E est la tension d’entrée. Déterminer la tension \(\underline{s}\) aux bornes du condensateur en régime sinusoïdal forcé.

Correction

Paramétrage du problème.
On va utiliser la loi des noeuds en terme de potentiel donc on va nommer les potentiels et choisir une référence des potentiels. Remarquons qu’on sait que \(\underline{V_A} = \underline{E}\) et on cherche \(\underline{V_D} = \underline{u_C} + 0\).

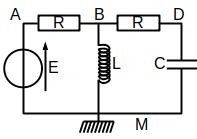
Application de la loi des noeuds en terme de potentiel
On va écrire deux lois des noeuds en termes de potentiel: en B et en D.

\[\begin{align*} &\begin{cases} \frac{\underline{V_B} - \underline{V_A}}{R} + \frac{\underline{V_B} - \underline{V_M}}{\underline{Z_L}} + \frac{\underline{V_B} - \underline{V_D}}{R} &= 0\\ \frac{\underline{V_D} - \underline{V_B}}{R} + \frac{\underline{V_D} - \underline{V_M}}{\underline{Z_C}} &= 0 \end{cases}\\ &\Longrightarrow \\ &\begin{cases} \frac{\underline{V_B} - E}{R} + \frac{\underline{V_B}}{j L \omega} + \frac{\underline{V_B} - \underline{V_D}}{R} &= 0\\ \frac{\underline{V_D} - \underline{V_B}}{R} + jC \omega \underline{V_D} &= 0 \end{cases}\\ &\Longrightarrow \\ &\begin{cases} \underline{V_B} = \left(1 + j RC \omega\right) \underline{V_D}\\ \left(2 + \frac{R}{jL\omega}\right)\underline{V_B} - \underline{V_D} = E \end{cases}\\ &\Longrightarrow \left(1 + j \left(2 RC\omega - \frac{R}{L\omega}\right) + \frac{R^2 C}{L}\right) \underline{V_D}= E\\ &\Longrightarrow \underline{s} = \underline{V_D} = \frac{E}{1 + j \left(2 RC\omega - \frac{R}{L\omega}\right) + \frac{R^2 C}{L}} \end{align*}\]

Vérification du résultat.

En régime sinusoïdal forcé, on peut remarquer que \(C \omega\) est homogène à l’inverse d’une résistance et que \(L \omega\) est homogène à une résistance. Vous pouvez vérifier aisément que les grandeurs calculées sont homogènes (on rappelle qu’une phase est sans dimension).

D’autres vérification seront possible lorsque nous aurons étudié les comportements asymptotiques.

Passage fréquentiel-temporel

Passage réel-complexe

On parle aussi de passer du temporel au fréquentiel et inversement : il suffit de remplacer les dérivées par es \(j\omega\).

Méthode: Du fréquentiel au temporel

Attention aux signes lorsqu’on passe du fréquentiel au temporel. En effet, le signe - pour le monôme de degré 2 vient en de \(j^2\) et doit disparaître (cf. exercice).

Passage du fréquentiel au temporel

On peut aussi faire l’inverse et déduire d’une étude des grandeurs complexes, l’équation différentielle qui le relit. Il faut (pour deux grandeurs s et e reliée):

1. mettre le rapport \(\frac{\underline{s}}{\underline{e}}\) sous forme d’une fraction de deux polynômes en \(\omega\): \(\frac{P(j\omega)}{Q(j \omega)}\).

2. mettre l’égalité sous la forme\(Q(j \omega) \underline{s} = P(j \omega)\underline{e}\).

3. Remplacer chaque facteur \((j\omega)^n\) par la dérivée \(\frac{\rm{d^n}}{\rm{dt^n}}\)

Exercice

On considère un système dont la relation entrée sortie entre les grandeurs complexes (on parle de fréquentiel) est:

\[ \frac{\underline{s}}{\underline{e}} = \frac{1 - jRC \omega}{1 - LC \omega^2 + j RC \omega} \]

Déterminer l’équation différentielle qui relie les grandeurs \(s(t)\) à \(e(t)\).

Correction

On commence par exprimer l’équation sous forme \(P(j\omega) \underline{s} = Q(j \omega) \underline{e}\) où P et Q sous des polynômes en \(j \omega\):

(53)\[\begin{equation} \underline{s} - LC \omega^2 \underline{s} + j RC \omega \underline{s} = \underline{e} - jRC \omega \underline{e} \end{equation}\]

On remplacer chaque terme en \(j \omega\) par une dérivée temporelle:

(54)\[\begin{equation} s + LC \frac{\rm{d^2}s}{\rm{dt^2}} + RC \frac{\rm{d}s}{\rm{dt}} = e - RC \frac{\rm{d}e}{\rm{dt}} \end{equation}\]

Etude fréquentielle

Analyse HF et BF

On considère le circuit RLC série ci-après. On veut étudier le comportement fréquentiel de certaines grandeurs. On rappelle qu’il s’agit d’étudier les caractéristiques du régime sinusoïdal forcé pour une entrée sinusoïdale quelconque.

Etudier la réponse haute et basse fréquence de l’intensité circulant dans le circuit et de la tension aux bornes du condensateur pour le circuit RLC série.

Correction

Etude basse fréquence
A basse fréquence, le condensateur se comporte comme un interrupteur ouvert et la bobine comme un fil. Le circuit est donc assimilable au circuit suivant:

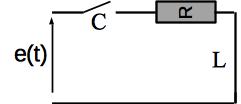
Il vient que l’intensité est nulle. La loi des mailles s’écrit alors \(u_C = e - Ri = e\).

Etude haute fréquence
A haute fréquence, le condensateur se comporte comme un fil et la bobine comme un interrupteur ouvert. Le circuit est donc assimilable au circuit suivant:

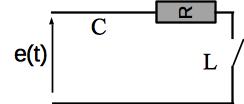
Il vient que l’intensité est nulle et la tension aux bornes du condensateur est nulle aussi (tension aux bornes d’un fil).