Etude d’un circuit linéaire#

Pour étudier un circuit linéaire (ie. trouver une ou plusieurs grandeurs du circuit), il existe différentes méthodes:

  • Utiliser les lois des noeuds et des mailles combinées (cf. l’exemple ici)

  • Utiliser une(des) loi(s) des noeuds traduites en terme de potentiel (cf. le même exemple)

  • Reconnaître et utilisée des ponts diviseurs comme présentés ci-dessous. Cette méthode est souvent combinée avec l’utilisation de résistances équivalentes.

Pont diviseur de tension#

Important

Pont diviseur de tension

Considérons N résistances en série dont les résistances sont \(\{R_i \vert i \in [\![1;n]\!]\}\) aux bornes de laquelle la tension est u.

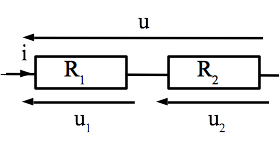
../_images/elec_resistance_serie.png

L’intensité circulant dans l’ensemble est:

\[ i = \frac{u}{\sum_{i=1}^{i=n} R_i} \]

Et la tension u se divise dans chaque dipôle. La tension aux bornes de la résistance \(R_k\) est:

\[ u_k = \frac{R_k}{\sum_{i=1}^{i=n} R_i} u \]

Démonstration

On peut utiliser l’additivité des tensions: \(u = \sum_{i=1}^{i=n} u_k = \sum_{i=1}^{i=n} R_k i = \) d’où l’expression de l’intensité.

De \(u_k = R_k i\), on obtient l’expression de la tension.

Cf. cet exemple pour savoir comment repérer un pont diviseur de tension.

Pont diviseur de courant#

Important

Pont diviseur de courant Considérons N résistances en parallèle dont les conductances sont \(\{G_i \vert i \in [\![1;n]\!]\}\) dans laquelle entre une intensité totale i.

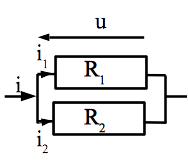
../_images/elec_resistance_parallele.png

La tension aux bornes de l’ensemble est:

\[ u = \frac{i}{\sum_{i=1}^{i=n} G_i} \]

Et le courant i se divise dans chaque branche. L’intensité aux bornes de la résistance \(R_k\) est:

\[ i_k = \frac{G_k}{\sum_{i=1}^{i=n} G_i} i \]

Démonstration

On peut écrire une loi des noeuds: \(i = \sum_{i=1}^{i=n} i_k = \sum_{i=1}^{i=n} G_k u = \) d’où l’expression de la tension.

De \(i_k = G_k u\), on obtient l’expression de l’intensité.