Association de résistances

Dipôle équivalent

Deux dipôles sont équivalents s’ils ont la même équation d’évolution

Comme l’indique la définition, la méthode principale pour démontrer ou déterminer une équivalence est de déterminer l’équation d’évolution des deux dipôles et de procéder à une identification des termes. Nous allons aussi des cas d’équivalence à connaître qui peuvent être utilisés directement.

Résistances en série

Généralisation

N résistances de valeurs \(\{R_i \vert i \in [\![1;n]\!]\}\) en série sont équivalentes à une seule résistance de valeurs \(R_{eq} = \sum_{i=1}^{i=n} R_i\)

Important

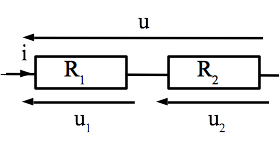
Résistance équivalente à deux résistances en série Deux résistances \(R_1\) et \(R_2\) en série sont équivalentes à une seule résistance de valeur \(R_{eq} = R_1 + R_2\)

Démonstration

Comme expliqué précédemment, il suffit d’exprimer l’équation d’évolution. Ici, les deux résistances étant en série, la tension aux bornes de l’ensemble est la somme des tensions aux bornes de chaque dipôle: \(u = u_1 + u_2 = R_1 i + R_2 i = (R_1 + R_2) i\)

L’équation d’évolution d’une résistance étant \(u = R_{eq} i\), on peut identifier les deux expressions avec \(R_{eq} = R_1 + R_2\).

Résistances en parallèle

Généralisation

N résistances dont les conductances sont \(\{G_i \vert i \in [\![1;n]\!]\}\) en parallèle sont équivalentes à une seule résistance dont la conductance est \(G_{eq} = \sum_{i=1}^{i=n} G_i\)

Important

Résistance équivalente à deux résistances en parallèle

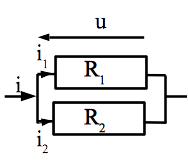
Deux résistances \(R_1\) et \(R_2\) en parallèle sont équivalentes à une seule résistance de valeur \(R_{eq} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2}}\) (soit de conduction \(G_{eq} = G_1 + G_2\))

Démonstration

Comme expliqué précédemment, il suffit d’exprimer l’équation d’évolution. Ici, les deux résistances étant en parallèle, l’intensité qui entre dans le dipôle complet est la somme des intensités circulant dans chaque dipôle: \(i = i_1 + i_2 = \frac{u}{R_1} + \frac{u}{R_2} = u (\frac{1}{R_1} + \frac{u}{R_2}) i\)

L’équation d’évolution d’une résistance étant \(i = u\frac{1}{R_{eq}}\), on peut identifier les deux expressions avec \(\frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2}\).