Exemple : Etude d’un système d’ordre 2
Contents
Exemple : Etude d’un système d’ordre 2#
Régime libre#
Nous allons étudier un exemple de système d’ordre 2 basé sur le circuit suivant (appelé circuit RLC série en régime libre) :
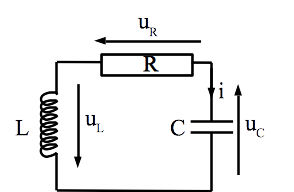
Cette fois, on suppose les conditions initiales connues à t=0 :
Mise en équation
Obtenir l’équation différentielle qui régit l’évolution de \(u_C(t)\) et la mettre sous forme canonique en utiliser le facteur de qualité.
Correction
On peut appliquer une loi des mailles: \(u_L + u_R + u_C = 0\) soit \(L \frac{\rm{d}i}{\rm{dt}} + Ri + u_C = 0\). Il reste à utiliser \(i = C \frac{\rm{d}u_C}{\rm{dt}}\), il vient en organisant):
(26)#\[\begin{equation} \frac{\rm{d^2}u_C}{\rm{dt^2}} + \frac{R}{L}\frac{\rm{d}u_C}{\rm{dt}} + \frac{1}{LC} u_C= 0 \end{equation}\]Il reste à identifier les facteurs:
\[\begin{align*} \omega_0^2 &= \frac{1}{LC} &\Longrightarrow& &\omega_0 &= \frac{1}{\sqrt{LC}}\\ \frac{\omega_0}{Q} &= \frac{R}{L} &\Longrightarrow& &Q &= \frac{1}{R}\sqrt{\frac{L}{C}} \end{align*}\]
Cas apériodique
Déterminer l’expression complète de \(u_C(t)\) avec les constantes d’intégration dans le cas d’un régime apériodique.
Correction
On a les expressions:
\[\begin{align*} u_C(t) &= A \exp^{r_1 t} + B \exp^{r_2 t}\\ i(t) = C \frac{\rm{d}u_C}{\rm{dt}} &= C A r_1 \exp^{r_1 t} + C B r_2 \exp^{r_2 t} \end{align*}\]soit les conditions initiales:
\[\begin{align*} u_C(t=0) &= A + B = 0 \Longrightarrow A = - B\\ i(t=0) &= C (r_1 - r_2) A = i_0 \Longrightarrow A = \frac{i_0}{C (r_1 - r_2)} \end{align*}\]Il vient les expressions:
\[\begin{align*} u_C(t) &= \frac{i_0}{C (r_1 - r_2)} \left (\exp^{r_1 t} - \exp^{r_2 t}\right ) \\\ i(t) = C \frac{\rm{d}u_C}{\rm{dt}} &= \frac{Ci_0}{C (r_1 - r_2)} \left ( r_1 \exp^{r_1 t} - r_2 \exp^{r_2 t} \right) \end{align*}\]
Cas critique
Déterminer l’expression complète de \(u_C(t)\) avec les constantes d’intégration dans le cas d’un régime critique.
Correction
On a les expressions:
\[\begin{align*} u_C(t) &= \exp^{r_0 t} \left ( At + B\right)\\ i(t) = C \frac{\rm{d}u_C}{\rm{dt}} &= C \exp^{r_0 t} \left ( r_0 A t + r_0 B + A\right) \end{align*}\]soit les conditions initiales:
\[\begin{align*} u_C(t=0) &= B = 0\\ i(t=0) &= C A = i_0 \Longrightarrow A = \frac{i_0}{C} \end{align*}\]Il vient les expressions:
\[\begin{align*} u_C(t) &= \frac{i_0}{C}\exp^{\omega_0 t} t\\ i(t) = C \frac{\rm{d}u_C}{\rm{dt}} &= i_0 \exp^{\omega_0 t} \left ( \omega_0 t + 1\right) \end{align*}\]
Cas pseudo-périodique
Déterminer l’expression complète de \(u_C(t)\) avec les constantes d’intégration dans le cas d’un régime pseudo-périodique.
Estimer une durée caractéristique du régime transitoire pour un régime pseudo-périodique et en déduire le nombre de pseudo-périodes qu’on peut voir. Commenter ce nombre quand \(Q\) devient grand.
Correction
Q1. On a les expressions:
\[\begin{align*} u_C(t) &= \exp^{-\lambda t}\left( A \sin^{\Omega t} + B \cos^{\Omega t}\right)\\ i(t) = C \frac{\rm{d}u_C}{\rm{dt}} &= C \exp^{-\lambda t}\left( \left(-\lambda A - \Omega B\right) \sin^{\Omega t} + \left(-\lambda B + \Omega A\right) \cos^{\Omega t}\right) \end{align*}\]soit les conditions initiales:
\[\begin{align*} u_C(t=0) &= B = 0\\ i(t=0) &= C \Omega A = i_0 \Longrightarrow A = \frac{i_0}{C \Omega} \end{align*}\]Il vient les expressions:
\[\begin{align*} u_C(t) &= \exp^{-\lambda t}\left( \frac{i_0}{C \Omega} \sin^{\Omega t}\right )\\ i(t) &= \exp^{-\lambda t}\left( -\lambda \frac{i_0}{\Omega} \sin^{\Omega t} + i_0 \cos^{\Omega t} \right) \end{align*}\]Q2. C’est le facteur \(\exp{-\frac{\omega_0 t}{2Q}}\) qui gouverne la décroissance en amplitude, le temps caractéristique est donc \(\tau_{carac} = \frac{2Q}{\omega_0}\) et l’exponentielle aura décru de 95% pour \(3 \tau_{carac}\).
La pseudo période a pour expression \(T = \frac{2\pi}{\Omega} = \frac{2 \pi}{\frac{\omega_0}{Q}\sqrt{4Q^2 - 1}}\). Il vient qu’on pourra observer un nombre de périodes:
(27)#\[\begin{equation} N_P = \frac{3 \tau_{carac}}{T} = \frac{3}{2\pi}\sqrt{4Q^2 - 1} \end{equation}\]Pour \(Q\) grand, il vient \(N_P \approx Q\). On observe que plus le facteur de qualité est grand, plus on observe de pseudo-périodes car le régime transitoire dure plus longtemps.
Réponse indicielle d’un RLC série#
Exercice
On considère le circuit suivant (E est constant). A t=0, le condensateur est complètement déchargé et aucun courant ne circule dans le circuit.
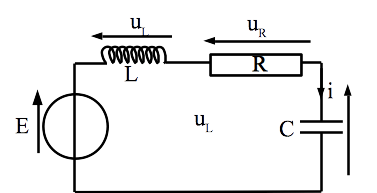
Exprimer la tension aux bornes du condensateur dans le nouveau régime forcé.
Déterminer l’équation différentielle qui régit l’évolution de la tension aux bornes du condensateur. En déduire les expressions du facteur de qualité et de la pulsation propre. Les comparer au cas du régime libre.
Déterminer l’expression de la tension aux bornes du condensateur pour t>0 dans le cas d’un régime pseudo-périodique.
Déterminer l’expression de la tension aux bornes du condensateur pour t>0 dans le cas d’un régime apériodique.
Déterminer l’expression de la tension aux bornes du condensateur pour t>0 dans le cas d’un régime critique.
Correction
Q1. Nouveau régime forcé
On peut considérer que le nouveau régime forcé est indépendant du temps (puisque E est constant). Le condensateur se comporte donc comme un interrupteur ouvert et l’intensité est donc nulle. Il vient que la tension aux bornes de la résistances est nulle.La bobine elle se comporte comme un fil. La loi des mailles donne donc que \(u_C(t=+\infty) = E\)
Q2. Mise en équation
On peut écrire la loi des mailles \(E = u_C + u_R + u_L = u_C + R i + L \frac{\rm{d}i}{\rm{dt}} = 0\). Soit avec \(i = C \frac{\rm{d}u_C}{\rm{dt}}\):(28)#\[\begin{equation} \frac{\rm{d^2}u_C}{\rm{dt^2}} + \frac{R}{L} \frac{\rm{d}u_C}{\rm{dt}} + \frac{1}{LC} u_C = \frac{1}{LC}E \end{equation}\]Il vient \(\omega_0 = \frac{1}{LC}\) et \(Q = \frac{1}{R}\sqrt{\frac{L}{C}}\) soit les mêmes expressions que dans le cas du régime libre. C’est normal puisqu’il s’agit du même système (RLC série) confronté à une entrée différente (nulle dans un cas et égale à E dans l’autre).
Q3. Expression temporelle - Cas pseudo-périodique
La solution générale ESSM est alors:(29)#\[\begin{equation} u_{c,0}(t) = D \exp^{-\frac{\omega_0 t}{2Q}} \left(\cos{\Omega t + \varphi} \right) \end{equation}\]avec \(\Omega = \omega_0 \sqrt{1 - \frac{1}{4Q^2}}\) la pseudo-pulsation du système.
On recherche une solution particulière de l’équation avec second membre. On la cherche sous forme constante \(u_C = U_0\). Les dérivées étant nulles, on trouve directement \(U_0 = E\). La solution complète est donc:
(30)#\[\begin{equation} u_{c}(t) = D \exp^{-\frac{\omega_0 t}{2Q}} \left(\cos{\Omega t + \varphi} \right) + E \end{equation}\]Il reste à utiliser les conditions initiales en utilisant le fait que \(i = C \frac{\rm{d}u_C}{\rm{dt}}\):
\[\begin{align*} u_{c}(t=0) &= D \cos{\varphi} + E = 0 \\ i(t = 0) &= C D \left(-\Omega \sin{\varphi} -\frac{\omega_0}{2Q} \cos{\varphi} \right) = 0\\ \Longrightarrow \varphi &= -\arctan{\frac{\omega_0}{2Q \Omega}} = -\arctan{\frac{1}{\sqrt{4Q^2 - 1}}}\\ \Longrightarrow D &= - \frac{E}{\cos{\varphi}} = - \frac{2Q}{\sqrt{4Q^2-1}}E \end{align*}\]Q4. Expression temporelle - Cas apériodique
La solution générale ESSM est alors:(31)#\[\begin{equation} u_{c,0}(t) = A \exp^{r_1 t} + B \exp^{r_2 t} \end{equation}\]avec \(r_{1,2} = -\frac{\omega_0}{2Q}(1 - \sqrt{1 - 4Q^2})\).
On recherche une solution particulière de l’équation avec second membre. On la cherche sous forme constante \(u_C = U_0\). Les dérivées étant nulles, on trouve directement \(U_0 = E\). La solution complète est donc:
(32)#\[\begin{equation} u_{c}(t) = A \exp^{r_1 t} + B \exp^{r_2 t} + E \end{equation}\]Il reste à utiliser les conditions initiales en utilisant le fait que \(i = C \frac{\rm{d}u_C}{\rm{dt}}\):
\[\begin{align*} u_{c}(t) = A + B + E = 0\\ u_{c}(t) = A r_1 + B r_2 = 0\\ \Longrightarrow A =-\frac{r_2}{r_2 - r_1}E\\ \Longrightarrow B =-\frac{r_1}{r_1 - r_2}E \end{align*}\]Q5. Expression temporelle - Cas critique
La solution générale ESSM est alors:(33)#\[\begin{equation} u_{c,0}(t) = \exp^{-\frac{\omega_0 t}{2Q}} \left(A t + B\right) \end{equation}\]avec \(r_{1,2} = -\frac{\omega_0}{2Q}(1 - \sqrt{1 - 4Q^2})\).
On recherche une solution particulière de l’équation avec second membre. On la cherche sous forme constante \(u_C = U_0\). Les dérivées étant nulles, on trouve directement \(U_0 = E\). La solution complète est donc:
(34)#\[\begin{equation} u_{c}(t) = \exp^{-\frac{\omega_0 t}{2Q}} \left(A t + B\right) + E \end{equation}\]Il reste à utiliser les conditions initiales en utilisant le fait que \(i = C \frac{\rm{d}u_C}{\rm{dt}}\):
\[\begin{align*} u_{c}(t) = B + E = 0 \Longrightarrow B = -E\\ u_{c}(t) = -\frac{\omega_0 }{2Q} B + A = 0 \Longrightarrow A = -\frac{\omega_0 }{2Q} E \end{align*}\]
Vérification
On rappelle les vérification d’usage : Nouveau régime permanent et homogénéité. Il est conseillé de vérifier aussi l’homogénéité au niveau de l’équation différentielle, de Q (sans dimension) et de \(\omega_0\).
Lorsqu’on détermine des conditions initiales, si le calcul est relativement complexe, il est aussi conseillé de vérifié qu’elles vérifient bien le système de départ.
