Entrainement : Régimes de fonctionnements
Contents
Entrainement : Régimes de fonctionnements#
Circuits d’ordre 1#
Circuit d’ordre 1
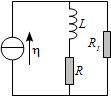
Calculer i, l’intensité qui circule dans la bobine. On donne \(i(t=0)=0\).
En déduire \(i_1\) et \(u_1\) (tension aux bornes de \(R_1\) et courant circulant dans \(R_1\)).
Tracer i et \(i_1\) en fonction du temps.
Point utile pour cet exercice
\(\Longrightarrow\) Conditions initiales.
\(\Longrightarrow\) Mise en équation.
Eléments de réponse (sans justification)
\(i(t) = \frac{R_1}{R_1 + R}\eta\left ( 1 - e^{- \frac{(R_1 + R)t}{L}}\right )\)
Deux condensateurs
On considère le circuit électrique de la figure ci-après. A t=0, \(q_1 = Q_1\) et \(q_2 = 0\). Donner l’évolution ultérieure (tensions et intensité) et faire un bilan énergétique.
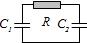
Point utile pour cet exercice
\(\Longrightarrow\) Conditions initiales.
\(\Longrightarrow\) Mise en équation.
Eléments de réponse (sans justification)
\(q_1(t) = Q_1 \frac{C_1}{C_1 + C_2} + Q_1 \frac{C_2}{C_1 + C_2}e^{-\frac{(C_1 + C_2)t}{RC_1 C_2}}\)
L’énergie stockée dans les deux condensateurs a globalement diminuée: elle correspond à l’énergie dissipée dans la résistance.
Circuit soumis à une rampe.
On branche en parallèle une bobine d’inductance \(L=10 \rm{mH}\) (non parcourue par un courant avant t=0), une résistance \(R = 1 \rm{k \Omega}\) et un générateur idéal de courant qui fournit une rampe de courant \(\eta\) de pente \(\lambda\) en partant de 0A et jusqu’à un courant \(I_0 = 1 \rm{A}\) (atteint pour un temps \(t_0\)) puis reste constant.
Établir l’équation d’évolution de \(i(t)\) le courant qui traverse la bobine quand le générateur débite une rampe de courant. Que vaut \(i(0^{+})\)?
Pour \(t < t_0\), chercher une solution particulière sous la forme \(i_O(t) = \alpha t + \beta\). En déduire \(i(t)\) pour \(t < t_0\) de l’équation.
Calculer \(t_0\) en fonction de \(\lambda\) et \(I_0\). Discuter suivant les valeur de \(\lambda\) et \(I_0\) les parts relatives données au régime transitoire et au régime “permanent” — on définira ces deux régimes.
On prend \(\lambda = 1 \rm{A.s^{-1}}\), quelle approximation peut-on faire? Que vaut \(i(t_0)\)? En déduire l’évolution de \(i(t)\) après \(t=t_0\).
Calculer l’énergie délivrée par le générateur pendant les deux périodes \(\left[0;t_0\right]\) et \(\left[t_0;+\infty\right]\). La comparer avec l’énergie délivrée par un générateur délivrant un échelon de courant \(I_0\) branché en parallèle à R et L. Commenter.
Point utile pour cet exercice
\(\Longrightarrow\) Conditions initiales.
\(\Longrightarrow\) Mise en équation.
Eléments de réponse (sans justification)
Toutes les intensités sont orientées vers le bas.
\(\frac{\rm{d}i}{\rm{dt}}(t) + \frac{R}{L} i(t) = \frac{R}{L}\eta(t)\).
\(i(t) = \lambda (t - \tau) + \lambda \tau e^{-t/tau}\) _(On pose \(i(t) = \alpha t + \beta\) puis on introduit cette forme dans l’équation différentielle ce qui donne \(\alpha t + (\alpha + \beta / \tau) = \lambda t\) soit par identification \(\alpha = \lambda\) et \(beta = -\lambda \tau\)).
On doit comparer \(t_0\) à \(\tau\). si \(t_0 \ll \tau\), l’exponentielle est devient presque négligeable et en \(t=t_0\), il ne reste que le régime forcé \(\lambda (t-\tau)\). Sinon, le régime transitoire représenté par l’exponentielle n’es tpas négligeable. \(\lambda t_0 = I_0\).
On peut considérer l’exponentielle négligeable dans la condition initiale en \(t = t_0\). \(i(t > 0) \approx I_0 - \lambda \tau e^{\frac{t_0 - t}{\tau}}\) car la solution générale de l’équation avec second member est \(I_0 + A e^{-t/\tau}\) et la condition initiale \(i(t_0) \approx \lambda (t - \tau)\) donne le résultat précédent. Note : on pourrait presque considérer que \(i(t=t_0)\approx I_0\) et alors l’intensité reste constante pour \(t>t_0\).
L’énergie trouvée est deux fois moins importante:
L’exponentielle dans la première intégrale donne une valeur négligeable et \(i(+\infty) - i(t_0) \approx 0\).
Circuits d’ordre 2#
Oscillateur faiblement amorti
On considère un circuit RLC série en régime libre. A \(t=0\), l’intensité circulant dans le circuit est \(I_0\) et la tension aux bornes du condensateur et nulle.
On suppose de plus que \(RC \ll \frac{L}{R}\).
Préciser le type de régime pour le système.
Dans l’approximation proposée, simplifier l’expression de la pseudo-pulsation.
Comparer le temps caractéristique du réigme transitoire et la pseudo-période du signal. En déduire l’allure graphique de q(t).
Déterminer l’expression complète de q(t).
Point utile pour cet exercice
\(\Longrightarrow\) Conditions initiales.
\(\Longrightarrow\) Mise en équation.
Eléménts de réponse (sans justification)
C’est un régime pseudo-périodique et la pseudo-pulsation est à peu près égale à la pulsation propre. Le temps caractéristique \(\frac{2Q}{\omega_0}\) est donc grand devant la pseudo-période (Q grand) donc on observe de nombreuses oscillations et une enveloppe exponentielle qui décroit lentement.
Protection d’un interrupteur
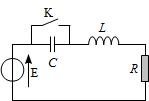
Dans le circuit ci-dessous, l’interrupteur K est fermé et à t=0, on l’ouvre.
Expliciter la tension \(u(t)\) aux bornes de K dans le cas où \(L/R>>RC\).
On donne \(L = 10 \rm{mH}, E = 5 \rm{V}, R = 50 \rm{\Omega}\). Évaluer la valeur maximale de \(u(t)\) en l’absence du condensateur (l’interrupteur a alors une propre capacité de 10pF). On attend de l’initiative dans les calculs.
Justifier l’emploi d’un condensateur. Déterminer la valeur de celui-ci pour limiter la valeur maximale de \(u(t)\) à 500V.
Point utile pour cet exercice
\(\Longrightarrow\) Conditions initiales.
\(\Longrightarrow\) Mise en équation.
Eléments de réponse (sans justification)
\(u(t) \approx e^{\frac{-\omega_0 t}{2Q}} (- E \cos(\omega_0 t) + QE\sin \omega_0 t) + E\) (à fort facteur de qualité, on doit trouver que la pseudo-pulsation égale la pulsation propre en première approximation).
\(u_{\max} \approx QE\) La tension obtenue est très grande: risque d’arc électrique. Le condensateur en parallèle augmente la valeur de C et diminue la surtension.
