Exemples d’étude
Contents
Exemples d’étude#
Etude d’un régime indépendant du temps.#
Cet exercice explique la méthode d’étude d’un régime indépendant du temps
Exercice
Étudier le circuit suivant en régime indépendant du temps lorsque l’interrupteur est ouvert. On déterminera toutes les intensités.
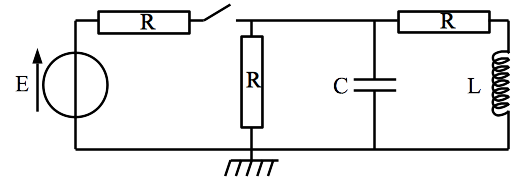
Correction
Mise en équation
On oriente toutes les intensités vers le haut dans chaque branche et on note respectivement \(i_e, i_r, i_c, i_l\) les intensités qui circulent dans la source, la résistance seule dans sa branche, le condensateur, la bobine.Dessiner le circuit équivalent en régime indépendant du temps
Tout d’abord, on redessine le circuit en utilisant les modèles équivalents au condensateur et à la bobine en régime indépendant du temps.
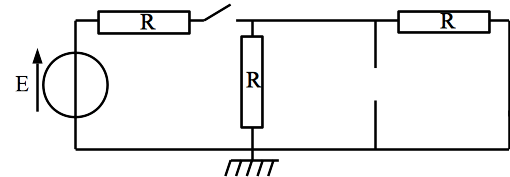
Il suffit ensuite d’étudier le circuit. Il vient directement \(i_e = i_c = 0\) à cause des interrupteurs ouverts.
On a donc \(i_r + i_l = 0\) et \(R i_r - R i_l = 0\) soit \(i_l = i_r = 0\)
Remarquons que seules deux tensions sont non nulles: la tension de la source (E) et la tension aux bornes de l’interrupteur de gauche (E ou -E suivant l’orientation).
Exercice
Etudier le circuit précédent en régime indépendant du temps lorsque l’interrupteur est fermé. On déterminera toutes les intensités.
Correction
Tout d’abord, on redessine le circuit en utilisant les modèles équivalents au condensateur et à la bobine en régime indépendant du temps.
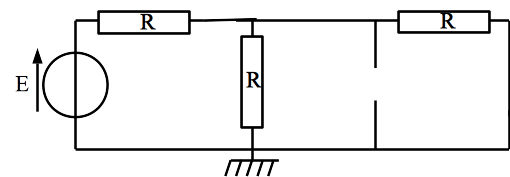
Il suffit ensuite d’étudier le circuit. Il vient directement \(i_c = 0\) à cause des interrupteurs ouverts.
Écrivons les lois de Kirchhoff (on pourrait aussi utiliser la loi des noeuds en terme de potentiels):
(35)#\[\begin{align} i_e + i_r + i_l &= 0\\ E - R i_e + R i_r &= 0\\ R i_r - R i_l &= 0 \end{align}\]Il vient immédiatement \(i_r = i_l\) et donc \(i_e = - 2 i_r\). La première loi des mailles s’écrivant alors \(E + 3 R i_R = 0\), il vient:
(36)#\[\begin{align} i_r &= -\frac{E}{3R}\\ i_l &= -\frac{E}{3R}\\ i_e &= \frac{2E}{3R}\\ \end{align}\]
Analyse des résultats
Homogénéité: Les intensités sont bien homogènes à des tensions sur des résistances.
Sens physique: Assez logiquement l’intensité \(i_e\) est positive (si E est positive car elle dans le sens de E) tandis que les deux autres sont négatives (sens inverse de E).
Sens physique: On a un pont diviseur de courant avec deux résistances identiques, on trouve logiquement l’égalité des intensités \(i_l = i_r\) et le fait que l’intensité \(i_e\) est le double des deux autres.
Caractéristiques d’un régime transitoire#
Régime apériodique - Temps de réponse
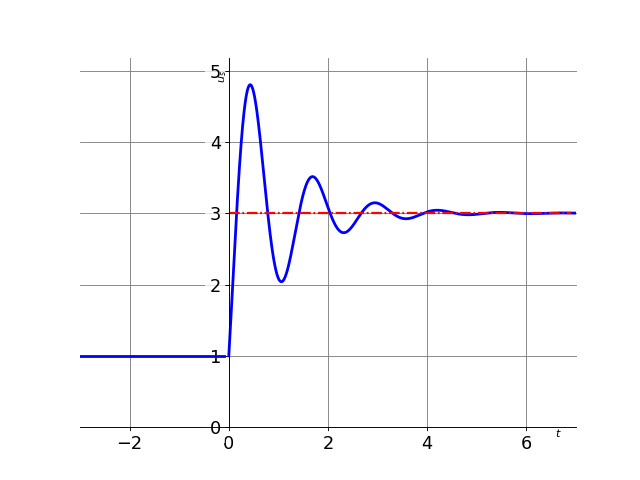
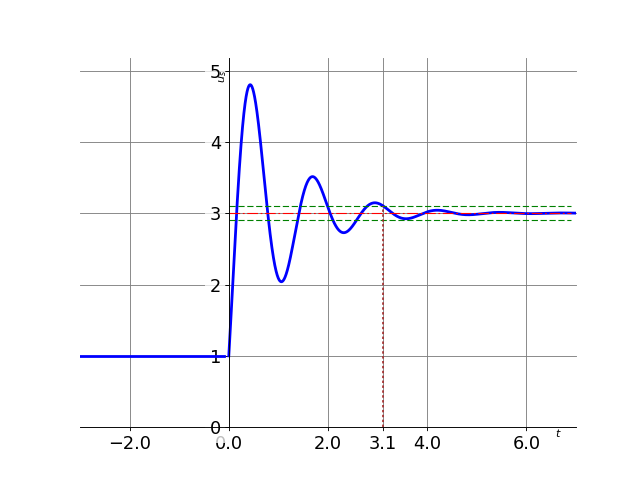
Déterminer le temps de réponse à 95% pour le signal dont l’évolution est représentée ci-dessous.
Correction
Détermination du temps de réponse
On détermine dans un premier temps l’écart initial: on commence à 1V et on finit à 3V. L’écart de 5% est donc de \((3 - 1 ) * 0.05 \% = 0.1V\) on regarde donc quand l’écart entre le signal et la valeur finale reste inférieur à 0.1V soit compris 2.9V et 3.1VL’instant correspond est de 3.1s. La perturbation arrivant à 0s, le temps de réponse est de 3.1s
Mise en équation d’un système#
Déterminer l’équation différentielle (Lois de Kirchhoff)#
On se propose ici de voir comment déterminer l’équation différentielle qui régit l’évolution d’une grandeur au moyen des lois de Kirchhoff.
Exercice
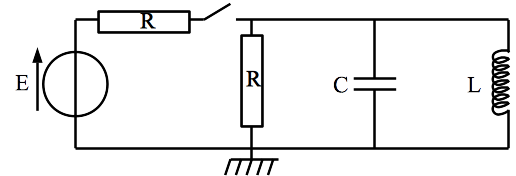
On considère le circuit suivant. L’interrupteur est ouvert depuis un temps long. A t=0, on ferme l’interrupteur.
Déterminer l’équation différentielle qui régit l’évolution de l’intensité qui circuledans la bobine pour \(t>0\).
Correction
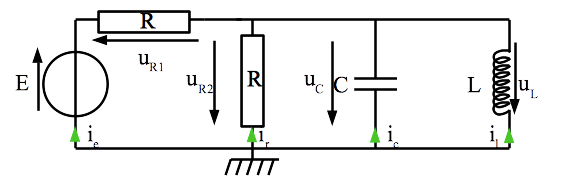
Paramétrage
Comme d’habitude, on commence par paramétrer le système. Les grandeurs introduites sont présentées sur le graphique.
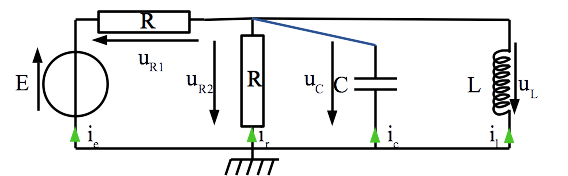
Rappelons aussi que les deux noeuds du haut peuvent être “rassemblés en un seul, ce qui évite d’avoir à considérer l’intensité qui circule dans la branche du haut au milieu.
Mise en équation
On utilise les lois de Kirchhoff. Les deux points à bien faire attention sont:
Bien déterminer quelle sont les grandeurs pour chaque relations : ce n’est pas juste i ou u, c’est l’intensité qui circule dans le condensateur (resp. dans la bobine) et la tension aux bornes du condensateur (resp. de la bobine).
Bien faire attention aux conventions. (Choisissez si vous pouvez des conventions récepteurs pour L, C et R).
Ne pas forcément vouloir éliminer toutes les tensions ou toutes les intensités. Cette fois, on ne peut pas toujours exprimer une tension en fonction d’une intensité ou vice-versa à cause des dérivées.
Il convient par contre de bien penser à faire la différence entre ce qui nous intéresse de ce qu’on veut éliminer.
(37)#\[\begin{align} i_e + i_r + C \frac{\rm{d}u_C}{\rm{dt}} + i_l &= 0 \\ E - R i_e + L \frac{\rm{d}i_l}{\rm{dt}} &= 0 \\ R i_r - L \frac{\rm{d}i_l}{\rm{dt}} &= 0 \\ u_C - L \frac{\rm{d}i_l}{\rm{dt}} &= 0 \end{align}\]On a 4 inconnues et 4 équations. Le système peut donc être résolu.
Manipulation du système
Une fois le système mis en place, il convient de réfléchir à une stratégie avant de se lancer (on rappelle que les grandeurs à éliminer sont les deux intensités ert \(u_C\)). Remarquons que le choix des mailles a permis d’avoir un système simple car chacune des lois des mailles permet d’élminer une grandeurs:(38)#\[\begin{align} i_e + i_r + C \frac{\rm{d}u_C}{\rm{dt}} + i_l &= 0 \\ i_e &= \frac{E + L \frac{\rm{d}i_l}{\rm{dt}}}{R}\\ i_r &= \frac{L \frac{\rm{d}i_l}{\rm{dt}}}{R} \\ u_C &= L\frac{\rm{d}i_l}{\rm{dt}} \end{align}\]Il suffit ensuire de remplacer dans la loi des noeuds (première équation) les différentes grandeurs.
(39)#\[\begin{equation} \frac{E}{R} \frac{L}{R}\frac{\rm{d}i_L}{\rm{dt}}+ \frac{L}{R}\frac{\rm{d}i_L}{\rm{dt}} + LC \frac{\rm{d^2}i}{\rm{dt^2}} + i_l = 0 \end{equation}\]Organisation de l’équation
Il convient d’organiser (en fonction des dérivées) l’équation correctement sous sa forme canonique.(40)#\[\begin{equation} \frac{\rm{d^2}i_L}{\rm{dt^2}} + \frac{2}{RC} \frac{\rm{d}i_L}{\rm{dt}} + \frac{1}{LC} i_L = -\frac{E}{RLC} \end{equation}\]Par identification avec la forme canonique, il vient:
(41)#\[\begin{equation} \begin{cases} \omega_0 &= \sqrt{\frac{1}{LC}}\\ \frac{\omega_0}{Q} = \frac{2}{RC} \Longrightarrow Q &= \frac{R}{2}\sqrt{\frac{C}{L}} \end{cases} \end{equation}\]
Analyse de l’équation
Homogénéité: Puisqu’une dérivée temporelle revient à diviser par un temps, on attend devant la dérivée première un facteur homogène à des \(s^{-1}\) (pour être homogène avec la dérivée seconde) et devant la fonction \(u_C\) un facteur homogène à des \(s^{-2}\).
On montrera que le produit RC est homogène à un temps (utiliser les équations d’évolutions de R et C). et que le produit LC est homogène à un temps au carré (idem). L’expression est bien homogène.
Sens physique: Le système est d’ordre 2. C’est ce qu’on attend d’un circuit possèdant un condensateur et une bobine.
Stabilité : Dans le système (sans la tension d’entrée), il n’y a que des dipôles passifs. On attend donc que le système soit stable. C’est effectivement ce qui est prédit par l’équation (signe des coefficients)
Nouveau régime forcé: Une autre vérification possible qui peut même faire l’objet d’une étude à part entière est le régime forcé. On rappelle qu’on peut en effet déterminer le régime forcé à partir du schéma. On trouve \(i_{L,force} = -\frac{E}{R}\) (s’entraîner à le prouver).
On peut retrouver un régime forcé indépendant du temps en cherchant une solution constante à l’équation différentielle précédente. Soit en cherchant \(i_L(t) = I_0\) l’équation \(0 + 0 + \frac{1}{LC} I_0 = -\frac{E}{RLC}\). On trouve bien la bonne expression: l’équation est cohérente.
Déterminer des conditions initiales#
Cet exercice explique comment déterminer les conditions initiales nécessaires à la résolution de l’équation différentielle. Il fait suite au précédent
Exercice
On considère le circuit. L’interrupteur est ouvert depuis un temps long. A t=0, on ferme l’interrupteur. On rappelle qu’on a déterminé l’équation différentielle pour \(i_L\) pour t > 0 (prendre les notations précédentes). Déterminer les conditions initiales nécessaires à la résolution de l’équation précédente.

Correction
On peut considérer qu’à \(t = 0^-\), le système est dans un régime forcé (avec l’interrupteur ouvert).
Quelles grandeurs déterminer dans l’ancien régime forcé (t<0)?
Le but n’est pas de caractériser entièrement l’ancien régime forcé mais de déterminer les grandeurs qui nous permettent d’avoir des informations sur les conditions initiales, c’est-à-dire sur __l’instant \(t=0^+\) : les grandeurs continues.Etude en \(t=0^-\) : L’étude de l’ancien régime permanent donne \(u_C(t=0^-) = 0\) (la bobine assimilable à un fil impose une tension nulle aux bornes du condensateur) et \(i_l(t=0^-) = 0\) (loi des noeuds avec \(i_C(t=0^-)=0\) (interrupteur ouvert) et \(i_R(t=0^-)=\frac{u_C(t=0^-)}{R}=0\)).
Ces grandeurs étant continues, il vient \(\boxed{i_l(t=0^+)= 0}\) et \(\boxed{u_C(t=0^+) = 0}\)
Etude du circuit à \(t=0^+\).
On chercher à obtenir la valeur de \(i_l(t=0^+)\) et de \(\frac{\rm{d}i_l}{\rm{dt}}(t=0^+)\) pour résoudre l’équation différentielle.
\(i_l(t=0^+) = 0\) (cf. supra)
\(\frac{\rm{d}i_l}{\rm{dt}}(t=0^+) = \frac{u_L(t=0^+)}{L} = \frac{u_C(t=0^+)}{L} = 0\)
On dispose donc des deux conditions initiales pour résoudre l’équation.
Exemple d’autres études#
Nous allons voir ici l’exemple d’autres études à partir soit de l’équation différentielle, soit de la forme temporelle. On rappelle qu’on peut aussi obtenir des information du circuit même (en régime forcé par exemple). Il est conseillé d’essayer de faire cet exercice avant de regarder la réponse.
Exercice
On traaille avec le même système que précédemment. On rappelle que l’équation qui régit l’évolution de i_L(t) est:
Conditions initiales: \(i_l(t=0^+) = 0\) et \(\frac{\rm{d}i_l}{\rm{dt}}(t=0^+) = 0\)
Déterminer \(i_l(t)\) dans l’hypothèse \(R > \sqrt{\frac{L}{C}}\).
En déduire la puissance reçue par le bobine p(t).
Déterminer l’énergie reçue par la bobine entre \(t=0\) et \(t=+\infty\).
Correction
Q1. Résolution de l’équation différentielle.
La solution générale de l’équation homogène est:(42)#\[\begin{equation} i_{l,0} (t) = {\exp}^{- \frac{t}{RC}} \left(A \cos \left(\sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} t \right) + B \sin \left(\sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} t \right)\right) \end{equation}\]On cherche une solution particulière constante à l’équation avec second membre \(i_{L,1}(t) = I_0\). L’équation à résoudre (les dérivées temporelles s’annulent):
(43)#\[\begin{equation} \frac{1}{LC} I_0 = - \frac{E}{RLC} \Longrightarrow I_0 = -\frac{E}{R} \end{equation}\]La solution générale de l’équation avec second membre (identique à l’exercice précédent) est donc:
(44)#\[\begin{equation} i_{l} (t) = {\exp}^{- \frac{t}{RC}} \left(A \cos \left(\sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} t \right) + B \sin \left(\sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} t \right)\right) - \frac{E}{R} \end{equation}\]Les conditions initiales donnent le système d’équations:
(45)#\[\begin{align} i_{l} (t=0^+) = A - \frac{E}{R} = 0 &\Longrightarrow A = \frac{E}{R}\\ \frac{\rm{d}i_l}{\rm{dt}} (t=0^+) = -\frac{E}{R^2C} + \sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} B = 0 &\Longrightarrow B = \frac{E}{R^2C\frac{1}{LC} - \frac{1}{{(RC)}^2}} \end{align}\]On en déduit l’expression de l’intensité \(i_l(t)\) et de la tension \(u_L(t)\):
(46)#\[\begin{align} i_{l} (t) &= {\exp}^{- \frac{t}{RC}} \left(\frac{E}{R} \cos \left(\sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} t \right) + \frac{E}{R^2C\sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}}} \sin \left(\sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} t \right)\right) - \frac{E}{R}\\ u_{L} (t) &= -\frac{EL}{R} {\exp}^{- \frac{t}{RC}} \left(\frac{1}{{(RC)}^2\sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}}} + \sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} \right) \sin \left(\sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} t \right) \end{align}\]
Vérification du résultat
S’entraîner comme précédemment à vérifier l’homogénéité du résultat et les informations physiques qu’on attend.
Q2. Puissance reçue
Nous sommes en convention récepteur donc la puissance reçue est:(47)#\[\begin{align} p(t) &= i_{l}(t) \times u_L(t) \\ &= - L I_A^2 \left ({\exp}^{- \frac{2t}{\tau}} \left(\cos \left(\Omega t \right) + \frac{1}{\tau \Omega} \sin \left(\Omega t \right)\right)\left(\frac{1}{\tau^2 \Omega} + \Omega \right ) \sin \left(\Omega t \right) - \right )\\ & \times {\exp}^{- \frac{t}{\tau}} \left(\frac{1}{\tau^2 \Omega} + \Omega \right ) \sin \left(\Omega t \right) \end{align}\]On a introduit les grandeurs suivantes : \(\tau = RC\) et \(\Omega =\sqrt{ \frac{1}{LC} - \frac{1}{{(RC)}^2}}\). Ce dernier terme est d’ailleurs très utilisé, on l’appelle la pseudo-période. Nous en reparlerons par la suite.
Q3. Variation d’énergie dans une bobine
Première méthode (mauvaise idée): intégrer l’expression précédente entre 0 et l’infini… … … On attendra pas un calcul aussi lourd (bien qu’il soit faisable et très formateur !).Deuxième méthode (à appliquer) : Il faut se rappeler que l’énergie reçue par la bobine est stockée et qu’on connaît l’expression de cette énergie stockée. Ainsi, l’énergie reçue sera la différence entre l’énergie stockée au final et l’énergie stockée initialement.
(48)#\[\begin{equation} \Delta E_L = E_L(t=+\infty) - E_L(t=0) = \frac{1}{2}L I(t=\infty)^2 - \frac{1}{2}L I(t=0)^2 = \frac{L E^2}{2R^2} \end{equation}\]
