Régime sinusoïdal forcé

Important

Régime sinusoïdal forcé Lorsqu’un circuit linéaire stable est soumis à une excitation sinusoïdale, le régime transitoire s’atténue au bout d’un temps et il s’établit un régime forcé appelé régime sinusoïdal forcé. Toutes les grandeurs variables du circuit ont alors la forme mathématique d’un sinusoïde de même pulsation que l’excitation.

Système stable et instable

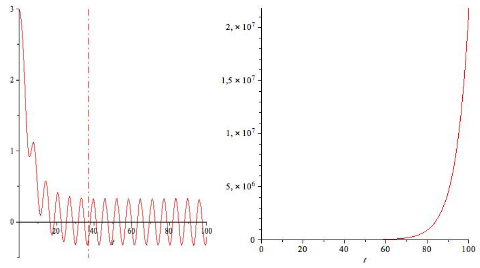
On a représenté ci-avant un système stable (gauche) tendant vers un régime sinusoïdal forcé et un système instable (droite) divergent.

Représentation complexe des signaux sinusoïdaux

Important

Représentation complexe d’un signal sinusoïdal

Considérons un signal sinusoïdal de la forme \(s(t) = s_m \cos (\omega t + \varphi)\). On définit la représentation complexe \(\underline s(t)\) du signal \(s(t)\) par la grandeur:

\[ \underline{s}(t) = s_m \exp j\left(\omega t + \varphi\right) \]

On définit aussi l’amplitude complexe \(\underline{s_m}\) du signal \(s(t)\) par la grandeur:

\[ \underline{s_m} = s_m \exp \left(j \varphi\right) = \frac{\underline{s}(t)}{\exp j \omega t} \]

Important

Relation complexe-réel. On a les relations suivantes:

\[\begin{align*} \textrm{Grandeurs réelle :} &s(t) = \Re \left (\underline{s(t)} \right) \\ \textrm{Amplitude (réelle) :} &s_m = \left\vert \underline{s_m} \right\vert = \left\vert \underline{s(t)} \right\vert \\ \textrm{Phase à l'origine :} &\varphi = \arg(\underline{s_m}) \end{align*}\]

Ces relations sont fondamentales car elles permettent de déduire les caractéristiques (amplitude et phase à l’origine) du signal réel (ce qui nous intéresse au final) connaissant la grandeurs complexes associées (ce qu’on déterminera en premier).

Opérations sur les grandeurs complexes

Important

Combinaison linéaire La représentation complexe de la combinaison linéaire de deux signaux de même pulsation est égale à la même combinaison linéaire des représentations complexes de deux mêmes signaux:

\[ s = \lambda_1 s_1 + \lambda_2 s_2 \Longrightarrow \underline{s} = \lambda_1 \underline{s_1} + \lambda_2 \underline{s_2} \textrm{ avec } (\lambda_1;\lambda_2) \in \mathbb{R}^2 \]

Ces dernières relations sont très utiles car nous allons pouvoir transformer l’étude d’équations différentielles en étude de polynômes.

Important

Dérivation et intégration La représentation complexe de la dérivée d’un signal sinusoïdal de pulsation \(\omega\) est égale à la représentation complexe du même signal sinusoïdal multiplié par \(j \omega\):

\[ \underline{\frac{\rm{d}s}{\rm{dt}}} = j \omega \underline{s} \]

La représentation complexe de la primitive - de valeur moyenne nulle - d’un signal sinusoïdal de pulsation \(\omega\) est égale à la représentation complexe du même signal sinusoïdal divisé par \(j \omega\):

\[ \underline{\int_s dt} = \frac{\underline{s}}{j \omega} \]

Démonstration (pour l’intégration)

On pose \(u(t) = A \cos \omega t + \phi\)

\[\begin{align*} \int u(t)dt &= \frac{A \sin(\omega t + \phi)}{\omega} = \frac{A \cos(\omega t + \phi - \frac{\pi}{2})}{\omega}\\ &\textrm{soit:}\\ \underline{\int u(t)dt} &= \frac{A e^{j(\omega t + \phi - \frac{\pi}{2})}}{\omega} = \frac{A}{j \omega} e^{j(\omega t + \phi)} = \frac{\underline{u}}{j \omega} \end{align*}\]

Intérêt des grandeurs complexes (en ligne)

Nous allons voir à travers l’étude du cas présenté précédemment l’intérêt de la grandeur complexe. Essayer de le résoudre avec les grandeurs réelles (on rappelle qu’on sait que le régime forcé est un régime sinusoïdal de même pulsation que l’entrée) puis passer à la correction pour voir l’utilisation des complexes.

Exercice

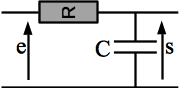
On rappelle qu’on étudie le circuit ci-après. Le point qui reste à prouver est l’étude fréquentielle, c’est-à-dire l’étude du régime sinusoïdal forcé par un sinusoïde quelconque de pulsation \(\omega\). On rappelle que le but est prouver que la tension aux bornes du condensateur pour une entrée de la forme \(e(t) = e_m \cos \omega t\)est de la forme:

\[ \frac{e_m}{\sqrt{1 + {\left(RC \omega\right)}^2}} \cos\left(\omega t - \arctan \left(RC \omega\right) \right) \]

Correction

Méthode: Passer l’équation différentielle en représentation complexe
Nous verrons par la suite qu’on peut directement étudier le circuit au moyen des représentations complexes. Pour l’instant, nous allons voir une première méthode, pas la plus efficace mais déjà plus performante que de rester avec les grandeurs réelles. Les méthodes plus directes seront présentées par la suite.

Phase à l’origine et déphasage

On a pris comme “origine des phases”, c’est-à-dire comme signal dont la phase à l’origine est nulle le signal d’entrée. C’est une pratique très fréquente (on ne peut le faire qu’avec un seul signal). Dès lors la phase à l’origine des autres grandeur (ici s) correspond au déphasage de cette grandeur par rapport à la tension d’entrée.

1. Obtention de l’équation différentielle: une loi des mailles en utilisant \(u_R = Ri = RC \frac{\rm{d}s}{\rm{dt}}\) donne: \(RC \frac{\rm{d}s}{\rm{dt}} + s = e\)

2. Passage aux grandeurs complexes: l’égalité des représentations complexes implique l’égalité de leurs parties réelles. On va donc prendre la représentation complexe de chaque terme de l’équation différentielle en gardant l’égalité. Résoudre cette égalité donnera une grandeur complexe dans la partie réelle est la solution cherchée. On va donc résoudre l’équation: \(\underline{RC \frac{\rm{d}s}{\rm{dt}} + s} = \underline{e}\), \(\underline{e}\) étant la représentation complexe de e, elle a pour expression \(e_m \exp j \omega t\). Remarquons au passage qu’on a ici choisit l’origine des phases pour l’ensemble du système: c’est la tension d’entrée.

3. Utilisation des propriétés des représentations complexes: on utilise les propriétés de linéarité et de la dérivée. L’équation se réécrit: \(j RC \omega \underline{s} + \underline{s} = \underline{e}\)

4. Résolution complexe: On obtient \(\underline{s} = \frac{\underline{e}}{1 + j RC \omega}\)

5. Passage aux grandeurs réelle: On obtient l’amplitude du signal en prenant le module de la représentation complexe: \(s_m = \frac{e_m}{\sqrt{1 + {(RC \omega)}^2}}\).

6. Passage à la grandeur réelle: On obtient la phase à l’origine en prenant l’argument de la représentation complexe: \(\varphi = - \arctan RC \omega\).

7. Passage à la grandeur réelle: La solution est donc: \(s(t) = \frac{e_m}{\sqrt{1 + {(RC \omega)}^2}} \cos (\omega t - \arctan RC \omega)\)

Mauvaise méthode: Utilisation des réelles (donc à ne PAS utiliser).
Insistons sur le fait que cette méthode n’est PAS à utiliser. Elle est présentée ici pour montrer que la résolution avec les complexes est plus simple.

On cherche un régime forcé sous la forme \(s(t) = s_m \cos \omega t + \varphi\). On l’introduit dans l’équation différentielle, ce qui donne:

\[ - RC \omega s_m \sin (\omega t + \varphi) + s_m \cos \omega t + \varphi = e_m \cos \omega t \]

soit en linéarisant:

\[ s_m \left(- RC \omega \cos \varphi - \sin \varphi\right) \sin \omega t + s_m \left(\omega \cos \varphi - RC \sin \varphi\right) \cos \omega t = e_m \cos \omega t \]

L’égalité étant vraie pour tout t, il vient que les coefficients devant chaque sinus et cosinus doivent être les mêmes:

\[\begin{align*} &\begin{cases} s_m \left(- RC \omega \cos \varphi - \sin \varphi\right) &= 0\\ s_m \left(\omega \cos \varphi - RC \omega \sin \varphi\right) &= e_m \end{cases}\\ &\Longrightarrow \\ &\begin{cases} s_m \cos \varphi \left( {\left(RC\omega \right)}^2 + 1 \right) &= e_m\\ s_m \sin \varphi \left( {\left(RC\omega \right)}^2 + 1 \right) &= - RC \omega e_m \end{cases}\\ \Longrightarrow \\ &\begin{cases} s_m^2 \left( {\left(RC\omega \right)}^2 + 1 \right)^2 &= e_m^2\\ \tan \varphi &= RC \omega \end{cases}\\ \end{align*}\]

La résolution des dernières équations redonne bien les mêmes solutions.

Simplicité des complexes
En conclusion, l’intérêt de l’introduction des grandeurs complexes et bien sa grande simplicité (qui va être encore simplifiée par l’étude directe du circuit avec les grandeurs complexes). On détermine en effet une seule inconnue (la représentation complexe ou l’amplitude complexe) au lieu de deux (amplitude et phase à l’origine) en utilisant des systèmes d’équations linéaires et non des égalités de fonctions trigonométriques.

Impédances complexes

Impédances complexes

Position du problème
Soit un dipôle linéaire passif. Dans un circuit en régime permanent sinusoïdal,

• il est parcouru par un courant \(i(t)=i_m \cos(\omega t + \phi_i)\) dont la représentation complexe est: \(\underline{i}(t)=i_m e^{j \phi_i} e^{j \omega t}\)

• la tension à ses bornes est \(u(t) = u_m \cos(\omega t +\phi_u)\) dont la représentation complexe est: \(\underline{u}(t)=u_m e^{j \phi_u} e^{j \omega t}\).

Ecriture complexe

On peut écrire: \(\underline{Z} = R + jX\) avec R et X réels. R est appelée la résistance du dipôle et X la réactance.

On peut écrire: \(\underline{Y} = G + jB\) où G et B sont des réels. G est appelé la conductance et B la susceptance.

On appelle impédance réelle \(Z\) le module de \(\underline{Z}\) et admittance réelle \(Y\) le module de \(\underline{Y}\).

Attention

On a \(\underline{Y} = \frac{1}{\underline{Z}}\) mais a priori \(R \neq \frac{1}{G}\) et \(X \neq\frac{1}{B}\)

Impédance et admittance complexe

*On définit l’impédance complexe d’un dipôle par la grandeur:

\[ \underline{Z} = \frac{\underline{u}}{\underline{i}} = \frac{\underline{u_m}}{\underline{i_m}} \]

Elle ne dépend pas du temps mais peut dépendre de la pulsation du signal d’entrée.

*On définit l’admittance complexe comme l’inverse de l’impédance complexe:

\[ \underline{Y} = \frac{1}{\underline{Z}} = \frac{\underline{i}}{\underline{u}} = \frac{\underline{i_m}}{\underline{u_m}} \]

Interprétation et intérêt de l’impédance complexe

• L’argument de l’impédance complexe définit le déphasage de la tension \(u\) par rapport à l’intensité \(i\).

• Le module de l’impédance complexe est le rapport des amplitudes réelles des deux grandeurs.

L’intérêt des impédances est qu’on peut traiter un circuit électrique en appliquant les lois de Kirchhoff directement avec les représentations complexes (car les lois de Kirchhoff sont linéaires) et en y introduisant des relations intensités-tension sous la forme \(\underline{u} = \underline{Z} \underline{i}\).

On pourra de même écrire: la loi des noeuds en terme de potentiels avec les représentations complexes des potentiels et les impédances(donc avec des condensateurs et bobines - cf. suite), les ponts diviseurs de tension et courant avec les impédances (donc avec des condensateurs et bobines dans les ponts) et on pourra associer des impédances comme on associe des résistances en série ou en parallèle.

Impédances des dipôles usuels

Remarque

• On remarquera que l’impédance d’un condensateur est un imaginaire pur négatif. Les dipôles plus complexes qui possèderont une partie imaginaire négative seront dit à “effet capacitif”.

• On remarquera que l’impédance d’une bobine est un imaginaire pur positif. Les dipôles plus complexes qui possèderont une partie imaginaire positive seront dit à “effet inductif”.

• On remarquera que l’impédance d’une résistance est un réel pur positif. La partie réelle des dipôles plus complexes représentera les effets résistifs.

Important

Impédances usuelles

• Cas d’une résistance: \(\underline{Z} = R\)

• Cas d’une bobine: \(\underline{Z} = j L \omega\)

• Cas d’un condensateur: \(\underline{Z} = \frac{1}{jC \omega}\)

Démonstration

Le cas de la résistance est triviale.

Pour la bobine, l’équation d’évolution s’écrit: \(u = L \frac{\rm{d}i}{\rm{dt}}\) soit en complexe \(\underline{u} = j L \omega \underline{i}\)

Pour le condensateur, l’équation d’évolution s’écrit: \(i = C \frac{\rm{d}u}{\rm{dt}}\) soit en complexe \(\underline{i} = j C \omega \underline{u}\)

Les exercices méthodes montrent l’utilisation des impédances.

Etude fréquentielle: Méthode et résultats importants

Etude haute et basse fréquence d’un circuit

Il est important de pouvoir analyser le comportement asymptotique d’un système, c’est-à-dire les comportements haute et basse fréquence. On peut pour celà utiliser deux méthodes:

• Etablir les équations et étudier le comportement limites des expressions complexes quand la pulsation tend vers 0 (basse fréquence) et vers l’infini (haute fréquence).

• Analyser directement le circuit en remplçant les condensateurs et bobines par des équivalents haute et basse fréquence. On parle d’étude rapide et l’on va préciser cette méthode.

Quantifier HF et BF.

En général dans les systèmes en physique, on arrive à exhiber une pulsation (et donc une fréquence) caractéristique appelée pulsation (fréquence) propre. Elle apparaît en général lorsqu’on veut mettre l’expression d’une grandeur sous une forme canonique (cf. suite).

• On considère généralement qu’une haute fréquence est une fréquence grande devant la fréquence propre.

• On considère généralement qu’une basse fréquence est une fréquence petite devant la fréquence propre.

Important

Comportements basse fréquence de C et L

A basse fréquence, un condensateur se comporte comme un interrupteur ouvert et une bobine comme un fil.

Démonstration

A haute fréquence, l’impédance du condensateur tend vers l’infini et celle de la bobine tend vers 0.

Important

Comportements haute fréquence de C et L

A haute fréquence, un condensateur se comporte comme un fil ouvert et une bobine comme un interrupteur.

Démonstration

A haute fréquence, l’impédance du condensateur tend vers 0 et celle de la bobine tend vers l’infini.

Cf. cet exemple

Formes canoniques

Il faut pouvoir déterminer quelle forme est applicable à la grandeur étudié puis mettre l’expression calculée sous la forme en identifiant les élements caractéristiques (pulsation propre et facteur de qualité). Pour choisir la forme à appliquer, il faut connaître l’ordre du système et les comportements haute et basse fréquence.

Important

Comportement passe-bas d’ordre 2 Pour une grandeur d’un système d’ordre 2 dont le comportement haute fréquence est nul et le comportement basse fréquence non nul, sa représentation complexe peut se mettre sous la forme:

\[ \underline{s} = \frac{A}{1 - {\left(\frac{\omega}{\omega_0}\right)}^2 + j \frac{\omega}{Q\omega_0}} = \frac{A}{1 - x^2 + j\frac{x}{Q}} \]

où \(x = \frac{\omega}{\omega_0} \) est appelée pulsation réduite (attention, elle est sans dimension!).

Important

Comportement passe-bande d’ordre 2 Pour une grandeur d’un système d’ordre 2 dont le comportement haute et basse fréquence est nul, sa représentation complexe peut se mettre sous la forme:

\[\begin{align*} \underline{s} &= \frac{A}{1 + j Q \left(\frac{\omega}{\omega_0} - \frac{\omega_0}{\omega}\right)} = \frac{A}{1 + jQ \left(x - \frac{1}{x}\right)}\\ &= \frac{A j\frac{\omega}{\omega_0 Q}}{1 - {\left(\frac{\omega}{\omega_0}\right)}^2 + j \frac{\omega}{\omega_0 Q}} = \frac{A j \frac{x}{Q}}{1 - x^2 + j \frac{x}{Q}} \end{align*}\]

où \(x = \frac{\omega}{\omega_0} \) est appelée pulsation réduite (attention, elle est sans dimension!).

D’autres formes seront données dans le chapitre suivant.