Application

Ces exercices d’application directe sont à faire à la suite du cours pour vérifier votre compréhension des méthodes. Vous pourrez confronter votre travail avec celui de vos camarades et poser des questions sur cet exercice en classe mais il ne sera pas donné de correction complète.

Généralités

Manipulation des complexes

Déterminer le module et la phase à l’origine des grandeurs réelles associées aux représentations complexes suivantes puis tracer leur représentation de Fresnel. (Les grandeurs non soulignées sont des réels positifs.)

\[\begin{align*} \underline{s} &= \frac{1 - j RC \omega}{1 + j RC \omega} e_m\\ \underline{s} &= \frac{1}{1 - LC \omega^2} e_m e^{-j \pi / 3}\\ \underline{s} &= \frac{- LC \omega^2}{1 - LC \omega^2 + j RC \omega} e_m\\ \underline{s} &= \frac{- K}{1 + j RC \omega} e_m\\ \underline{s} &= j RC \omega e_m e^{j \varphi}\\ \underline{s} &= \frac{1 + j RC \omega}{1 - {(RC\omega)}^2 + j RC \omega} e_m \end{align*}\]

Point utile pour cet exercice

• \(\Longrightarrow\) Manipulation des complexes.

Modélisation d’une impédance

On considère un dipôle dont l’impédance se met sous la forme \(\underline{Z} = R + j X\) avec R et X réels.

1. Montrer que si X est positif, le dipôle peut être modélisé par une inductance en série avec une résistance donc on exprimera les valeurs en fonction de R, X et \(\omega.\)

2. Montrer que si X est négatif, le dipôle peut être modélisé par un condensateur en parallèle avec une résistance donc on exprimera les valeurs en fonction de R, X et \(\omega.\)

Point utile pour cet exercice

• \(\Longrightarrow\) Manipulation des complexes.

• \(\Longrightarrow\) Impédances usuelles.

Eléments de réponse (sans justification)

• Si X est positif, \(R_{eq} = R\) et \(L_{eq} = X / \omega\)

• Si X est négatif, \(R_{eq} = R + \frac{X^2}{R}\) et \(C_{eq} = -\frac{1}{\omega}\frac{X}{R^2 + X^2}\)

Passage temporel-fréquentiel

A partir des équations différentielles ci-dessous, exprimer la représentation complexe \(\underline{s}\) dans un régime sinusoïdal forcé à la pulsation \(\omega\).

\[\begin{align*} \frac{\rm{d^2}s}{\rm{dt^2}} + \frac{3R}{L} \frac{\rm{d}s}{\rm{dt}} + \frac{4}{{(RC)}^2} s &= 2 RC \frac{\rm{d}e}{\rm{dt}}\\ 4LC \frac{\rm{d^2}s}{\rm{dt^2}} + 2 RC \frac{\rm{d}s}{\rm{dt}} + K s &= K' e\\ 4LC \frac{\rm{d^2}s}{\rm{dt^2}} + 2 \frac{L}{R} \frac{\rm{d}s}{\rm{dt}} + K s &= K' LC \frac{\rm{d^2}e}{\rm{dt^2}} \end{align*}\]

Eléments de réponse (sans justification)

\[\begin{align*} \left(-\omega^2 + 3j \frac{R}{L}\omega + \frac{4}{{\left(RC\right)}^2}\right) \underline{s}&= 2j RC \omega \underline{e}\\ \left(-4LC\omega^2 + 2jRC \omega + K\right) \underline{s}&= K' \underline{e}\\ \left(-4LC\omega^2 + 2j\frac{L}{R} \omega + K\right) \underline{s}&= -\omega^2 K'LC \underline{e} \end{align*}\]

Passage fréquentiel-temporel

Déduire des équations ci-dessous les équations différentielles qui relient s et e. Discuter alors de la stabilité de chaque système

\[\begin{align*} \frac{\underline{s}}{\underline{e}} &= \frac{1 + jRC \omega}{1 - {(RC\omega)}^2 + 3 RC \omega}\\ \frac{\underline{s}}{\underline{e}} &= \frac{- {(RC \omega)}^2}{1 - LC\omega^2 + j RC \omega}\\ \frac{\underline{s}}{\underline{e}} &= \frac{{(RC \omega)}^2}{1 - LC\omega^2 - j RC \omega}\\ \frac{\underline{s}}{\underline{e}} &= \frac{K}{1 - 3j RC \omega}\\ \frac{\underline{s}}{\underline{e}} &= \frac{KjRC \omega}{1 + 3j RC \omega} \end{align*}\]

Eléments de réponse (sans justification)

Piège ! La première fraction n’est pas assimilable à un système linéaire réel, elle ne le serait que s’il y avait un j dans le troisième terme du dénominateur: \(3jRC \omega\), l’équation temporelle serait alors:

\[\begin{align*} LC \frac{\rm{d^2}s}{\rm{dt^2}} + RC \frac{\rm{d}s}{\rm{dt}} + s &= e + RC \frac{\rm{d}e}{\rm{dt}}\\ LC \frac{\rm{d^2}s}{\rm{dt^2}} + RC \frac{\rm{d}s}{\rm{dt}} + s &= {(RC)}^2\frac{\rm{d^2}e}{\rm{dt^2}}\\ LC \frac{\rm{d^2}s}{\rm{dt^2}} - RC \frac{\rm{d}s}{\rm{dt}} + s &= -{(RC)}^2\frac{\rm{d^2}e}{\rm{dt^2}}\\ -3 RC \frac{\rm{d}s}{\rm{dt}} + s &= Ke \textrm{ On notera qu'il s'agit d'un système instable.}\\ 3 RC \frac{\rm{d}s}{\rm{dt}} + s &= K RC \frac{\rm{d}e}{\rm{dt}} \end{align*}\]

Etude d’une réponse

Circuit RL

On considère un dipôle constitué d’une résistance R et d’une bobine d’inductance L en série. Il est branchée aux bornes d’une tension d’entrée e. Exprimer la tension aux bornes de la bobine en régime forcé lorsque la tension d’entrée est:

1. Cas 1 : \(e(t) = e_1 \cos{\omega_1 t} + e_2 \cos{(\omega_2 t + \varphi)} \)

2. Cas 2 : \(e(t) = e_1 \sin{\omega_1 t} + e_2 \sin{(\omega_2 t + \varphi)} \)

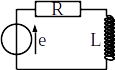
• On devra mélanger deux méthodes: l’utilisation des complexes déterminer le régime sinusoïdal forcé puis en déduire la réponse complète en utilisant la linéarité du système.

• Pour le cas des sinusoïdes, pensez qu’on peut prendre la partie imaginaire pour avoir une méthode simple d’étude.

Point utile pour cet exercice

• \(\Longrightarrow\) Etude d’un circuit en RSF

• \(\Longrightarrow\) Réponse d’un filtre linéaire

• \(\Longrightarrow\) Manipulation des complexes

Eléments de réponse (sans justification)

\(s(t) = \frac{\frac{\omega_1}{\omega_0}e_1}{\sqrt{1 + {\left ( \frac{\omega_1}{\omega_0}\right )}^2}} \cos {\left ( \omega_1 t - \arctan \frac{\omega_1}{\omega_0} + \frac{\pi}{2}\right )} + \frac{\frac{\omega_2}{\omega_0}e_1}{\sqrt{1 + {\left ( \frac{\omega_2}{\omega_0}\right )}^2}} \cos {\left ( \omega_2 t - \arctan \frac{\omega_2}{\omega_0} + \frac{\pi}{2} + \varphi\right )}\)

\(s(t) = \frac{\frac{\omega_1}{\omega_0}e_1}{\sqrt{1 + {\left ( \frac{\omega_1}{\omega_0}\right )}^2}} \sin {\left ( \omega_1 t - \arctan \frac{\omega_1}{\omega_0} + \frac{\pi}{2}\right )} + \frac{\frac{\omega_2}{\omega_0}e_1}{\sqrt{1 + {\left ( \frac{\omega_2}{\omega_0}\right )}^2}} \sin {\left ( \omega_2 t - \arctan \frac{\omega_2}{\omega_0} + \frac{\pi}{2} + \varphi\right )}\)

avec \(\omega_0 = \frac{R}{L}\)

Etude fréquentielle

RLC parallèlle

On considère trois dipôles R, L et C branchés en parallèle. On alimente le dipôle ainsi formé par un source modélisée par un modèle de Thévenin de résistance r et de force électromotrice E sinusoïdale. On étudie le régime sinusoïdal forcée.

Étudier la réponse fréquentielle pour l’intensité circulant dans la bobine et la tension aux bornes du dipôle RLC.

Point utile pour cet exercice

• \(\Longrightarrow\) Etude d’un circuit en RSF

• \(\Longrightarrow\) Résonance et bande passante

Eléments de réponse (sans justification)

Vous devez trouver un comportement “passe-bas” pour l’intensité dans la bobine et un comportement passe-bande pour la tension.