Entrainement : Bases

Puissance et énergie

Dipôles linéaires passifs

Calculer la puissance instantanée reçue puis l’énergie emmagasinée durant une période pour:

1. un condensateur C dont la tension à ses bornes est $u(t)=u_m\cos (\omega t+\varphi )$

2. une bobine L dont l’intensité la traversant est $i(t)=i_m\cos (\omega t+\varphi )$

3. une résistance R dont la tension à ses bornes est $u(t)=u_m\cos (\omega t+\varphi )$

Réponse (sans justification)

On trouve que la variation d’énergie sur une période pour la bobine et le condensateur sont toutes les deux nulle (propriété importante de C et L en régime périodique).

Pour la résistance, c’est un piège: elle n’emmagasine pas d’énergie…

Accumulateurs

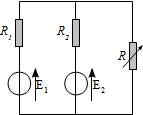
On considère le circuit suivant où R est une résistance variable et les fem $E_1$ et $E_2$ sont positives et $E_1>E_2$. Déterminer suivant les valeurs de R le comportement recepteur ou générateur deux fem.

Réponse (sans justification)

Valeur critique de R: $R_{eq}=\frac{R_1{E}_2}{E_1-E_2}$. Pour $R_{eq}<R$, $E_2$ a un comportement récepteur et pour $R_{eq}>R$, $E_2$ a un comportement générateur. $E_1$ a toujours un comportement générateur.

Point utile pour cet exercice

• $⟹$ Ponts diviseurs.

• $⟹$ Lois de Kirchoff.

• $⟹$ Puissance électrique.

Applications des lois de Kirchoff

Circuit divers

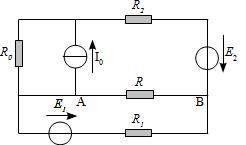
On considère le circuit ci-dessous. Déterminer l’intensité i qui traverse la résistance R (de la gauche vers la droite) en utilisant

1. les lois des noeuds et des mailles

2. la loi des noeuds en termes de potentiels

Réponse (sans justification)

$i=-\frac{R_1{E}_2+R_1{R}_0{I}_0+(R_0+R_2)E_1}{(R_0+R_2)(R_1+R)+R{R}_1}$

Point utile pour cet exercice

• $⟹$ Loi des noeuds en terme de potentiel.

• $⟹$ Lois de Kirchoff.

Ohmètre à tarage shunt

On considère le montage suivant qui modélise un ohmmètre à tarage shunt. Il comporte un générateur de f.e.m. E (de résistance interne négligeable), un milliampèremètre de résistance interne r, un rhéostat de résistance variable $R_h$ et des résistors $R_1,R_2$. La résistance X est la résistance à mesurer.

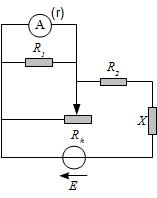
1. Exprimer l’intensité i dans le milliampèremètre en fonction de $E,R_1,R_2,R_h,r,X$. Quelle est cette intensité $i_0$ lorsque B et C (bornes de X) sont court-circuités?

2. L’avantage du tarage shunt est qu’on peut choisir $R_h$ très grande devant r. Donner dans ce cas l’expression de i sous la forme $\frac{kE}{X+R}$ en déterminant k et R.

3. En déduire l’expression de X en fonction de $i,i_0$ et R.

Réponse (sans justification)

$i=\frac{R{R}_h}{(R_2+X)(r{R}_1+R_1{R}_h+r{R}_h)+r{R}_1{R}_h}E$

$k=\frac{R}{R_1+r}$

$R=R_2+\frac{R_{1}r}{R_1+r}$

$X=R(\frac{i_0}{i}-1)$

Point utile pour cet exercice

• $⟹$ Ponts diviseurs.

• $⟹$ Lois de Kirchoff.

Dipôles équivalents

Générateur équivalent

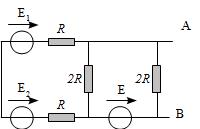
On considère le circuit suivant.

1. Déterminer le générateur de Thévenin du circuit équivalent entre les bornes A et B.

2. Donner la valeur de E pour laquelle le circuit est équivalent à une résistance pure (entre A et B) dont on précisera la valeur. A.N.: $R=5\mathrm{\Omega };{\mathrm{E}}_1=2\mathrm{V};{\mathrm{E}}_2=8\mathrm{V}$

Réponse (sans justification)

$E_{eq}=\frac{E_1-E_2-2E}{3}$

$R_{eq}=\frac{3R}{2}$

Maillage carré

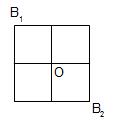
On considère le maillage suivant où chaque segment est une résistance R. Déterminer la résistance équivalente pour le dipôle pris entre $B_1$ et $B_2$ puis entre $O$ et $B_2$.

Réponse (sans justification)

$R_{B_1{B}_2}=\frac{3}{2}R$

$R_{O{B}_2}=\frac{7}{8}R$

Point utile pour cet exercice

• $⟹$ Lois de Kirchoff.

• $⟹$ Dipôles équivalents.

Résistances d’entrée et de sortie

Transistor bipolaire

Un transistor bipolaire est un tripôle qui est toujours utilisé comme un quadripôle en rendant une de ses électrodes communes à l’entrée et la sortie. En régime linéaire basse fréquence, les équations d’un transistor bipolaire en émetteur commun E sont: $u_{be}=r{i}_B+\mu u_{ce}$ et $i_C=\beta i_B+\frac{u_{ce}}{\rho }$. On désire déterminer les valeurs des différentes grandeurs données dans l’équation.

1. *Modéliser ce composant à l’aide de composants fondamentaux.

2. On place ensuite un générateur idéal de courant entre B et E et un ampèremètre à la place du générateur de tensions entre C et E. Pour un courant de 10,00mA en entrée, on mesure au multimètre un courant de 0,9981 A. Grâce à une protocole adapté, on mesure $r=2000\mathrm{\Omega }$ et $\rho =20,00\mathrm{k}\mathrm{\Omega }$. \begin{enumerate}1. Déterminer le gain en tension et le gain en courant.

3. Connaissant les valeurs de $\mu$ et $\beta$, proposer un protocole expérimental pour mesurer les valeurs de $r$ et $\rho$.

4. L’impédance d’entrée d’un voltmètre étant de $1\mathrm{M}\omega$ et la chute de tension maximale de l’ampèremètre de 0,2V, a-t-on eu raison de les considérer comme idéaux?

5. Calculer l’amplification $A=\frac{i_c}{i_b}$ quand un résistor $R_L$ est connecté entre les bornes C et E. A.N.: $R_L=1\mathrm{k}\mathrm{\Omega }$