Méthodes d’étude
Contents
Méthodes d’étude#
Les corrections sont en ligne.
Calculer une intensité par des considérations microscopiques.#
Cette méthode ne sera pas souvent utilisée dans ces chapitres mais est très utile pour comprendre le passage du microscopique au macroscopique.
Exercice
Estimer le nombre d’électrons par unité de volume pouvant participer à la conduction électrique. On donne :
Masse molaire du cuivre : \(M_{Cu} = 63.5 \rm{g.mol^{-1}}\)
Masse volumique du cuivre : \(\rho_{Cu} = 9 \times 10^3 \rm{kg.m^{-3}}\)
Correction
Les atomes de cuivre qui composent le métal ne perdent en général qu’un ou deux électrons pour former des ions. On peut donc considérer qu’il y a pour un atome de cuivre, un électron de conduction. La densité d’électron de conduction est donc du même ordre de grandeur que la densité d’atomes de cuivre.
\(n_{e} = n_{Cu} = N_A \frac{\rho_{Cu}}{M_{Cu}} = 6 \times 10^{23} \times \frac{9 \times 10^3}{63.5 \times 10^{-3}} = 10^{29} \rm{electrons.m^{-3}}\)
Exercice
On considère un fil de cuivre de section \(S = 1 \rm{mm^2}\) parcourue par une intensité \(I = 1 \rm{A}\). Estimer la vitesse des électrons en considérant qu’ils ont tous la même vitesse. Commenter cette vitesse.
Correction
Comptons combien d’électrons traversent une section \(S\) durant un temps \(\Delta t\)
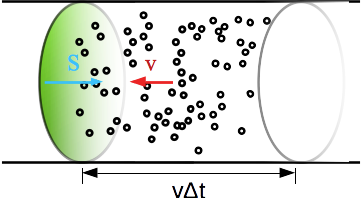
Fig. 15 Quantité de charge#
Considérons l’instant initial \(t\) et cherchons quelles sont les caractéristiques d’un électron qui va traverser la surface S entre t et \(t + \Delta t\). Il doit (avec les conventions de vitesse choisis sur le schéma - inverser la vitesse des électrons ne changerait pas la valeur de i en valeur absolue, cela ne ferait que changer le signe) :
être à droite (sur le schéma) de la section S
être à une distance inférieure à \(v \Delta t\) de la section S car la distance qu’il va parcourir est \(v \Delta t\)
Si ces deux conditions sont réunis, l’électron va immanquablement traverser la section S donc tous les électrons qui se trouvent dans le cylindre de base S et de hauteur \(v \Delta t\) à l’instant t traverseront la section S entre t et \(t + \Delta t\).
Utilisons la question précédente, la quantité d’électrons est : \(N_{e-} = -n_{e} S v \Delta t\) (le signe - vient du fait que les électrons se déplacent dans le sens inverse de l’orientation de la section) donc l’intensité est :
\(i = \frac{\Delta q}{\Delta t} = \frac{- (-e) n_{e} S v \Delta t}{\Delta t} = n_e e S v\)
Il vient une vitesse :
\(v = \frac{i}{n_e e S} = \frac{1}{\times 10^{29} \times 1.6 \times 10^{-19} \times 10^{-6}} = 6 \times 10^{-5} m.s^{-1}\)
On remarque que la vitesse est très faible, surtout comparée aux vitesses d’agitation thermique qui sont de l’ordre de plusieurs centaines de mètre par seconde. La conduction thermique correspond donc plutôt à une lente dérive des électrons tandis qu’ils s’agitent dans tous les sens.
Etudier un circuit électrique linéaire#
Par les lois de Kirchhoff#
Le but de cet exercice est d’apprendre à mettre en application tout ce qui a été vu précédemment. Nous utiliserons deus méthodes : la loi des noeuds en terme de potentiel. On pourra néanmoins s’entraîner à reprendre l’exercice en utilisant des tensions et la loi des mailles.
Exercice
On considère le circuit ci-dessous. Déterminer la tension \(U_{BC}\).
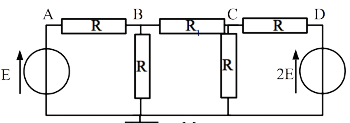
Correction - Lois des noeuds en terme de potentiel
On commence par paramétrer le système. On a au passage choisi une référence des potentiels (masse) au point M puisqu’on compte utiliser la loi des noeuds en terme de potentiel.
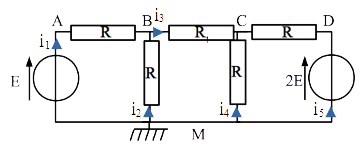
On écrit les lois des noeuds en différents points (il y a ici 3 noeuds car les deux du bas peuvent être regroupés, on écrit donc deux loi des noeuds):
On exprime les intensités en fonction des potentiels en utilisant les équations des dipôles:
On élimine les potentiels non recherchés (ici, on cherche \(U_{BC} = V_B - V_C\), on va donc éliminer \(V_A, V_D\) et \(V_M\)):
Il vient:
Réorganisons le système pour le résoudre.
soit en résolvant le système (s’entraîner impérativement à le faire):
d’où une tension:
Vérification du résultat
Homogénéité: On a bien une tension multipliée par un rapport de résistances, soit une tension.
Correction - Lois des mailles et des noeuds
On va travailler avec des tensions. On paramètre les intensités et tensions.
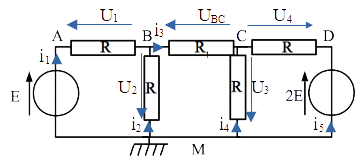
On a théoriquement 10 inconnues, mais on peut remarquer que chaque intensité est reliée à une tension par une relation \(i_i = U_i / R\) (ou \(R_1\)). Il reste donc 5 inconnues les 5 tensions. Il faut donc 5 équations : 3 lois des mailles et 2 lois de noeuds. Il vient (s’entraîner repérer de quel/le maille/noeud il est question et établir la loi correspondante):
soit en éliminant les intensités:
Il reste à éliminer successivement les tensions qui ne nous intéressent pas pour avoir à la fin une équation en \(U_{BC}\) seule. On trouve (s’entrainer à le faire):
Repérer et utiliser un pont diviseur de tension#
Le but de cet exercice est d’apprendre à utiliser un pont diviseur de tension. La méthode peut s’appliquer aussi au cas d’un pont diviseur de courant.
Exercice (très classique)
Déterminer la condition reliant les résistance pour que la tension \(U_{AB}\) soit nulle (on dit que le pont est alors équilibré).
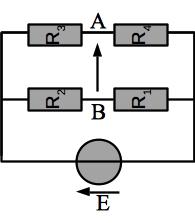
Fig. 16 Pont de Wheatstone#
Correction
Analyse du problème.
La grandeur qu’on doit exprimer est ici la tension \(U_{AB}\). On doit l’exprimer en fonction des grandeurs connues à savoir les résistances et E.
Il n’y a pas obligation d’utiliser un pont diviseur de tension mais le but est ici de montrer comment on l’applique.
On a (on a orienté toutes les tensions \(U_{Ri}\) de la droite vers la gauche comme E) : \(U_{AB} = U_{R4} - U_{R1}\). C’est pour calculer ces deux tensions qu’on peut utiliser des ponts diviseurs de tension.
Application d’un pont diviseur de tension.
On doit :
Repérer les résistances qui sont en série et repérer la tension au bornes du pont.
Repérer la résistance dont on veut déterminer la tension et appliquer la formule du pont diviseur de tension. Attention à l’orientation des tensions car la tensions \(U_k\) doit être orientée dans le même sens que la tension globale (ici E) pour appliquer la formule du pont.
Les résistance \(R_1\) et \(R_2\) sont en série : elles forment un pont diviseur de tension dont la tension aux bornes est E. Cela nous permet de calculer \(U_{R1}\):
Les résistance \(R_3\) et \(R_4\) sont en série : elles forment un pont diviseur de tension dont la tension aux bornes est E. Cela nous permet de calculer \(U_{R4}\):
Équilibre du pont
Il vient :
Le pont est donc équilibré quand :
Dipôles équivalents#
Dipôle équivalent par les équations d’évolution#
On se propose ici de voir comment déterminer un dipôle équivalent plus simple (une résistance ) à partir d’un maillage. On verra aussi l’utilisation des symétries.
Exercice
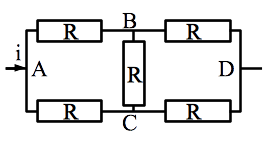
Déterminer la résistance équivalente au réseau de résistance ci-contre.
Correction
On va déterminer la relation tension-intensité. Mais pour simplifier le problème, remarquons que le maillage est symétrique par rapport à l’axe du fil. Cela implique que toutes le grandeurs sont symétrique. Ainsi, le potentiel au point B et au point C sont égaux et les intensités circulant dans les branches AB et AC (ou BD et CD) sont égales.
La loi des noeuds en A et D implique immédiatement que \(i_{AB} = i_{AC} = i/2 = i_{BD} = i_{CD} = i/2 \) (on a orienté les intensités en cohérence avec l’ordre des indices).
On peut maintenant calculer la tension entre A et D en fonction de i en passant par un chemin (par exemple le chemin ABD):
\(u_{AD} = u_{AB} + u_{BD} = R i/2 + R i/2 = R i\)
Par identification (\(u = R_{eq} =i\)), il vient que la résistance équivalente au maillage est R.
Dipôle équivalent par manipulation des schémas#
On se propose ici de voir comment déterminer un dipôle équivalent plus simple (une résistance ) à partir d’un maillage. Nous utilisons cette fois des transformations successives des circuits basés sur les résistances équivalentes établies précédemment.
Exercice
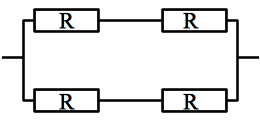
Déterminer la résistance équivalente au réseau de résistance ci-contre.
Exemple d’application
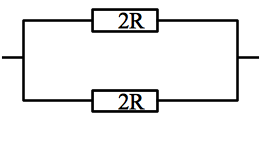
On remarque que dans chaque branche, les deux résistances R sont en série, donc équivalente à une résistance 2R.
On remarque que dans chaque branche, les deux résistances 2R sont en parallèle, donc équivalente à une résistance \(R_{eq} = \frac{1}{\frac{1}{2R}+\frac{1}{2R}} = R.\)
Donc le dipôle est équivalent à une seule résistance de valeur R.
Déterminer un modèle de Thévenin équivalent#
Cet exercice propose d’apprendre à montrer qu’un dispositif peut être remplacé par un modèle de Thévenin en déterminant ses caractéristiques. Nous étudierons deux méthodes: l’établissement de l’équation d’évolution comme utilisé précédemment pour la détermination d’un dipôle équivalent et le calcul de deux points particuliers.
Exercice
Montrer que le circuit ci-dessous est équivalent à un modèle de Thévenin entre les bornes A et B dont on déterminera les caractéristiques.
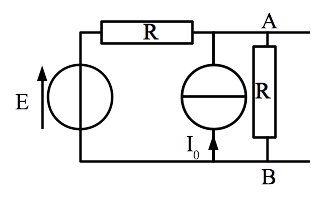
Correction
On commence par paramétrer le circuit et à bien réfléchir aux grandeurs:
qu’on doit chercher. Ici on veut exprimer la relation tension-intensité. On va donc chercher u en fonction de i ou i en fonction de u. Pour des raisons totalement arbitraires, on décide chercher u en fonction de i.
qu’on connaît: la fem E, le cem \(I_0\), la valeur de résistance R. L’intensité i devient aussi une grandeur qu’on “connait” puisqu’on veut exprimer u en fonction de i.
les grandeurs qui restent doivent être éliminées (il n’est même pas utile de les déterminer en fonction des données du problème puisqu’elle ne sont pas utiles à l’étude demandée). En général, ce sont des grandeurs que nous avons introduites, ici \(i_1, u_1, i_2\)
On a donc 4 inconnnues (\(u, i_1, u_1, i_2\)). Il faudra donc quatre équations.
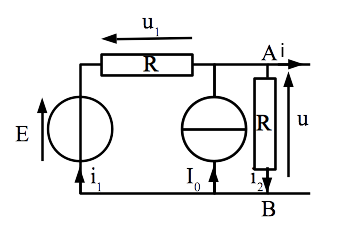
Orientation des grandeurs
On a orienté i et u en convention générateur de manière à pouvoir identifier la relation u(i) à la relation attendue du modèle de Thévenin en convention générateur \(u = E_{Th} - R_{Th} i\)
On a orienté \(i_2\) de cette façon pour que la résistance soit en convention récepteur. Le but est de pouvoir utiliser directement la loi d’Ohm (écrite en convention récepteur) sans se tromper dans les signes. Encore une fois, le choix de la convention étant arbitraire, on aurait pu choisir une convention générateur. Il est judicieux de choisir une convention récepteur, non pas pour des raisons physiques, mais pour ne pas se tromper dans les formules…
On réalise la mise en équation (nous utilisons ici les lois des mailles et des noeuds mais il est vivement conseillé de s’entraîner à cet exercice en appliquant la loi des noeuds en terme de potentiel):
(9)#\[\begin{align} i_1 + i_0 &= i + i_2\\ E - u_1 - u &= 0 \end{align}\]Avec les deux lois d’Ohm \(u_1 = R i_1\) et \(u = R i_2\) on dispose de 4 équations donc d’autant d’équations que inconnues.
La règle principale est d’éliminer les grandeurs qui ne nous intéresse pas ET DE GARDER JUSQU’AU BOUT LA GRANDEUR QU’ON VEUT CALCULER.. Ici, on va éliminer \(u_1\) et \(i_2\) en utilisant les lois d’Ohm. Il vient :
(10)#\[\begin{align} i_1 + i_0 &= i + \frac{u}{R}\\ E - R i_1 - u &= 0 \end{align}\]En multipliant par R la première équation et en sommant, il vient:
Par identification, on trouve:
(11)#\[\begin{align} E_{Th} &= \frac{E + R i_0}{2}\\ R_{Th} &= \frac{R}{2} \end{align}\]
Correction - Autre méthode
On propose d’utiliser une autre méthode pour déterminer les caractéristiques du modèle de Thévenin équivalent. Le principe est basé sur le fait qu’une caractéristique statique d’un dipôle linéaire est une droite. Il suffit donc de connaître deux points de la droite pour connaître ses caractéristiques.
On va choisir deux points simples à étudier:
Le cas où l’on impose i = 0 (on parle de coupe-circuit). On cherche u.
Le cas où l’on impose u = 0 (on parle de court-circuit). On cherche i.
Cas i = 0
La loi des noeuds s’écrit \(i_1 + i_0 = i_2 = \frac{u}{R}\)La loi des mailles s’écrit: \(E - R i_1 = u\)
Une combinaison linéaire pour éliminer \(i_1\) donne \(E + R i_0 = 2 u\)
Cas u = 0
La loi des noeuds s’écrit \(i_1 + i_0 = i + i_2 = i\)La loi des mailles s’écrit: \(E - R i_1 = u = 0\)
Une combinaison linéaire pour éliminer \(i_1\) donne \(E + R i_0 = R i\)
Synthèse. La droite du modèle de Thévenin doit donc passer par les points \((0;\frac{E}{R} + i_0)\) et \((\frac{E + R i_0}{2}; 0)\)
On cherche une droite de la forme \(u = E_{Th} - R_{Th} i\) passe par les deux point précédents (attention les coordonnées sont (u ; i)).
Une recherche mathématique classique du coefficient directeur donne \(R_{Th} = R / 2\).
La valeur de la fem est directement donnée au point i=0.
Etudes énergétiques#
Déterminer les comportements récepteurs/générateurs graphiquement.#
Il s’agit d’apprendre le principe de base de l’étude des comportements générateurs et récepteurs d’un dipôle et d’observer aussi que ces comportements peuvent changer en régime variable.
Exercice
On considère un dipôle D dans un circuit. Les évolutions de l’intensité qui le traverse et de la tension à ses bornes en convention générateur sont données ci-après. Déterminer les temps récepteurs et les temps générateurs, c’est-à-dire les moments où le dipôle se comporte comme un récepteur et les moments où le dipôle se comporte comme un générateur.
Remarque : pour cet exercice, peu importe quelle courbe représente l’intensité ou la tension.
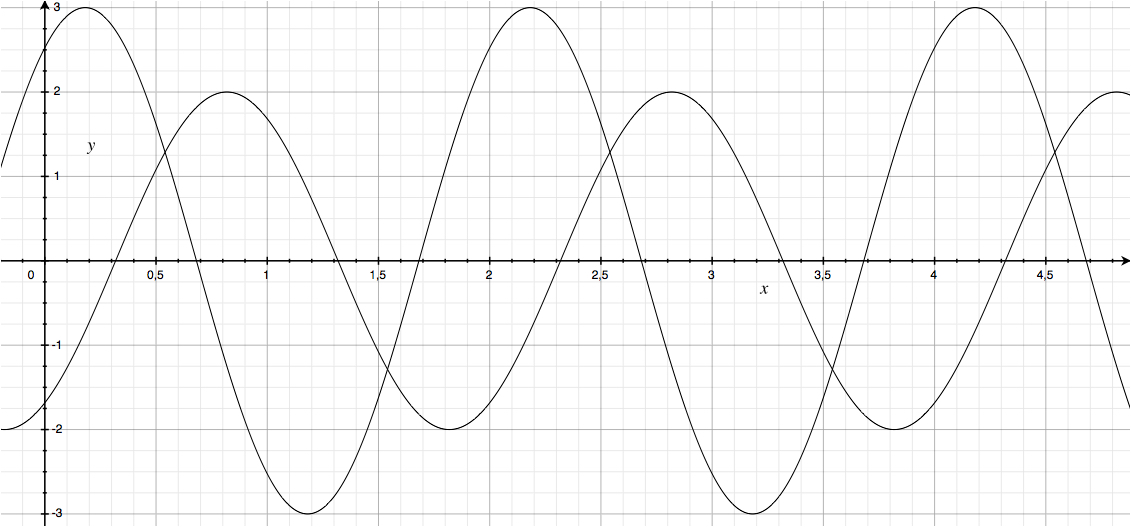
Correction
On rappelle que le comportement d’un dipôle est basé sur le signe de la puissance échangée en déterminant si celle-ci est fournie ou reçue.
Nous sommes en convention générateur, le produit \(ui\) est donc la puissance fournie par le dipôle au circuit. Si elle est positive (u et i sont de même signe), le dipôle se comporte comme un générateur, si elle est négative (u et i sont de signes opposés), le dipôle se comporte comme un récepteur.
On a ainsi pu représenter les instants générateurs (en vert) et récepteurs (en jaune) sur le graphique.
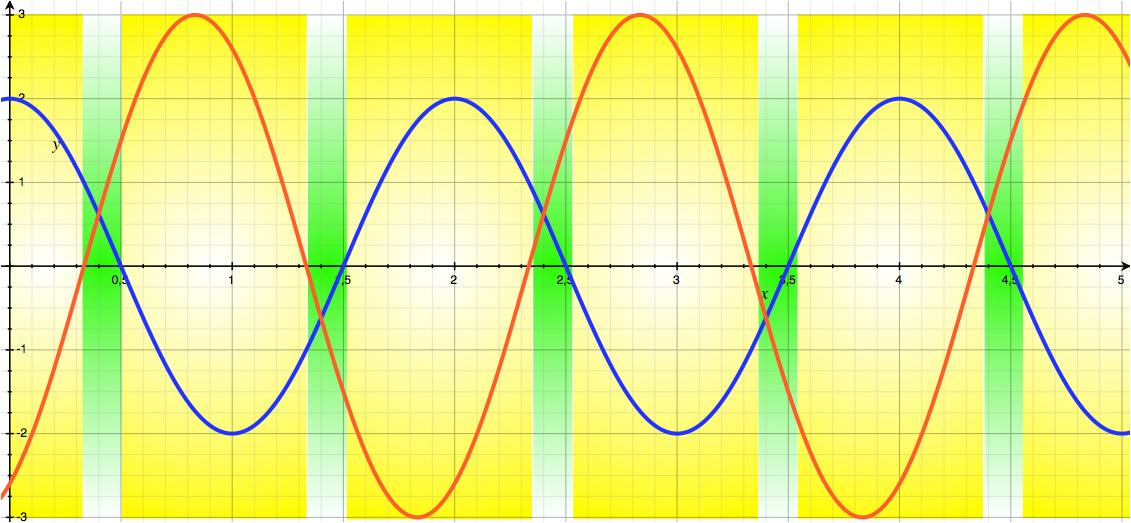
Remarque
Le dipôle ne se comporte toujours comme un récepteur ou un générateur, il peut passer d’un comportement à un autre.
Le signe des tensions et intensités ne détermine pas le comportement physique, c’est bien le signe du produit qui est important.
La durée des temps générateurs et récepteurs ne permet pas de dire seule si le dipôle fournit globalement (sur le temps long de toute l’expérience) de l’énergie ou s’il reçoit globalement de l’énergie. Il faudrait l’expression mathématique de u et i (ici vraisemblablement des sinusoïdes). Nous allons voir comme procéder pour déterminer des comportements globaux qui conduisent à une étude en énergie et non en puissance. Ici, on montrerait que le dipôle se comporte globalement comme un récepteur. Mais cela ne rend pas faux, le choix de la convention générateur.
Déterminer analytiquement les comportements générateurs/récepteurs#
Il s’agit ici de voir comment déterminer une puissance instantanée puis l’énergie échangée durant une période donnée. Les équations données ici correspondent au dipôles étudiées précédemment.
Exercice
On considère un dipôle D orientée en convention générateur. On a trouvé que l’intensité qui circulait dans le dipôle a pour expression : \(i(t) = i_m \sin(\pi t - \frac{\pi}{3})\) et que la tension à ses bornes est \(u(t) = u_m \sin(\pi t + \frac{\pi}{2})\) avec \(u_m > 0\) et \(i_m > 0\)
Exprimer la puissance instantanée \(p(t) = u(t) i(t)\). S’agit-il d’une puissance reçue ou fournie ?
Montrer que \(p(t)\) est un signal sinusoïdal dont on précisera les caractéristiques. On note T la période de \(p(t)\)
Déterminer l’énergie fournie par le dipôle durant une période T. Le dipôle a-t-il un comportement globalement générateur ou récepteur ?
Correction
Q1. Calcul de la puissance instantanée
\(p(t) = i_m u_m \sin(\pi t - \frac{\pi}{3}) \sin(\pi t + \frac{\pi}{2})\).Nous sommes en convention générateur, donc \(p(t)\) est la puissance fournie par le dipôle au circuit.
Il s’agit d’utiliser les formules trigonométriques (à connaitre). Ainsi :
\[\begin{align*} p(t) &= i_m u_m \sin(\pi t - \frac{\pi}{3}) \sin(\pi t + \frac{\pi}{2})\\ &= \frac{i_m u_m}{2} \left ( - \cos(2 \pi t + \frac{\pi}{6}) + \cos(\frac{5 \pi}{6}) \right ) \end{align*}\]\(p(t)\) est donc bien sinusoïdal et ses caractéristiques sont :
amplitude : \(\frac{i_m u_m}{2} \)
pulsation : \(2 \pi \rm{rad.s^{-1}}\) donc période 1s et fréquence 1Hz (on remarquera que ce n’est pas la période de u et i)
phase à l’origine : \(\frac{\pi}{6} + \pi\) (à cause du signe moins)
valeur moyenne : \(\frac{i_m u_m}{2}\cos(\frac{5 \pi}{6})\)
Q3. Calcul d’énergie
On rappelle la relation \(p = \frac{dE}{dt}\) où p est la puissance instantanée et E l’énergie (ici l’énergie échangée avec le circuit). On obtient donc l’énergie échangée par intégration de \(p(t)\) sur une période (\(T = 1s\)):\[\begin{align*} E = \int_{t=0}^{t=T} p(t) dt = \int_{t=0}^{t=T} \frac{i_m u_m}{2} \left (- \cos(2 \pi t + \frac{\pi}{6}) + \cos(\frac{5 \pi}{6}) \right )dt\\ E = \frac{i_m u_m}{2} \left [ -\frac{1}{2 \pi} \cos(2 \pi t + \frac{\pi}{6}) \right ]_{t=0}^{t=T} + \frac{i_m u_m}{2} \cos(\frac{5 \pi}{6}) T\\ E = \frac{i_m u_m}{2} \cos(\frac{5 \pi}{6}) T < 0 \end{align*}\]Le dipôle fournit globalement une énergie négative, c’est-à-dire qu’il reçoit une énergie \(\vert E \vert\): il est donc globalement récepteur.
Remarque
Attention, il faut se rappeler qu’il peut y avoir des temps où le dipôle possède un comportement générateur. Mais globalement, il reçoit de l’énergie plus qu’il n’en fournit.
Déterminer les comportements de dipôles dans un circuit#
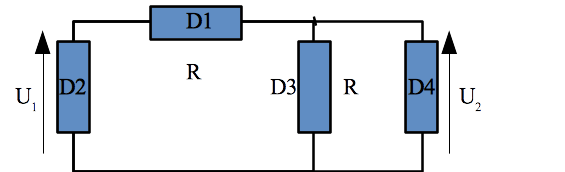
On travaille ici en régime indépendant du temps de manière à pouvoir utiliser simplement les lois de Kirchhoff. On considère le circuit ci-après et on donne les caractéristiques suivantes :
\(D_2\) et \(D_4\) sont des accumulateurs : leur tension est imposées de l’extérieur. La tension \(U_1\) aux bornes de \(D_2\) est connue et positive. La tension \(U_2\) est réglable (mais constante durant la manipulation) et de signe quelconque.
\(D_1\) et \(D_3\) sont deux conducteurs ohmiques : en convention récepteur la relation intensité-tension est : \(u = Ri\)
Exercice
Déterminer, suivant les valeurs de \(U_2\) les comportements récepteurs/générateurs des deux dipôles \(D_2\) et \(D_4\).
Correction
Comme on l’a vu précédemment, il faut choisir déterminer le signe de la puissance échangée. Pour cela, il faut :
Paramétrer le circuit en nommant les intensités et tensions (ou potentiels) mises en jeu. En effet, contrairement à l’exercice précédent où nous avons utiliser les lois de Kirchhoff, toutes les grandeurs ne sont pas explicitement définies. Et ce sera en général le cas.
Mettre en équation le problème en utilisant les relations intensités-tension et les lois de Kirchhoff.
Identifier la(les) grandeur(s) qu’on cherche, identifier les grandeurs qu’on connaît (les données de l’énoncé qu’on peut utiliser dans le résultat final) et les grandeurs qu’on a introduit nous même (et qui doivent être éliminées).
On résout le système en cherchant à obtenir ce qu’on veut.
On veut utiliser ensuite ce qu’on appelle une loi des noeuds en terme de potentiel, on paramètre donc des intensités et des points de potentiels puis nous devrons:
Ecrire la loi des noeuds voulues
Ecrire les intensités en fonction des potentiel si c’est possible.
Exprimer les potentiels en fonction eds grandeurs connues ou recherchées.
On en profite aussi pour choisir un point de potentiel nul (la masse). On prend \(V_M = 0\).
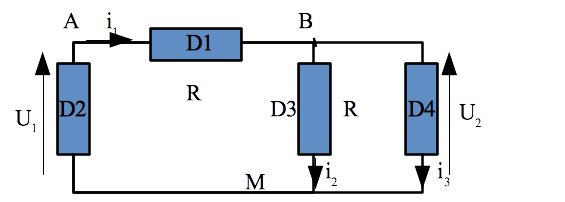
La loi des noeuds s’écrit \(i_1 = i_2 + i_3\) or :
\[\begin{align*} i_1 = \frac{U_{AB}}{R} = \frac{V_A - V_B}{R} = \frac{U_1 - U_2}{R}\\ i_2 = \frac{U_{BM}}{R} = \frac{V_B - V_M}{R} = \frac{U_2}{R}\\ i_3 = ? \end{align*}\]Remarque : il arrive que certaines intensités ne soient pas exprimables en fonction des potentiels.
*De plus : \(V_B = U_2 + V_M = U_2\) et \(V_A = U_1 + V_M = U_1\) Il vient :
(12)#\[\begin{equation} \frac{U_1- U_2}{R} =\frac{U_2}{R} + i_3 \end{equation}\]Il convient de se demander que doit-on calculer. Cette étape est fondamentale car son absence est souvent cause de beaucoup d’erreurs. Elle peut être faite avant ou après le paramétrage et souvent avant même la mise en équation. (On la fait ici pour profiter des grandeurs nommées).
On cherche : les puissances échangées par \(D_2\) (\(p_2\)) et \(D_4\) (\(p_4\)) et plus exactement leur signe. Ce sont les grandeurs dont on doit trouver une “formule” en fonction du reste.
On connaît: Les grandeurs connues sont : \(R, U_1\) et \( U_2\) qui sera notre paramètre variable pour l’étude des signes des puissances. Ces grandeurs pourront appraître dans les “formules” finales qu’on veut établir.
Toutes les autres grandeurs doivent disparaître.
4.
Les puissances s’expriment comme : \(p_2 = U_1 i_1\) et \(p_4 = U_2 i_3\) donc c’est la connaissance de \(i_1\) et \(i_3\) qui est importante (et surtout leur signe).On a directement :
\(i_3 = \frac{U_1 - 2 U_2}{R}\) et \(i_1 = i_2 + i_3 =\frac{U_1 - U_2}{R}\)
On remarque que \(i_3\) change de signe pour \(U_2 = \frac{U_1}{2}\) et \(i_1\) change de signe pour \(U_2 = U_1\). Nous allons utiliser un tableau de signe pour faire la synthèse des résultats et déterminer les signes de \(p_2\) et \(p_4\).
Attention : pour analyser ces signes, il faut avoir conscience des conventions d’orientation : \(D_2\) est en convention générateur, on calcul donc une puissance fournie. \(D_4\) est en convention récepteur, on calcule donc une puissance reçue.

Vérification et interprétation des résultats.
Il s’agit de conseil de relecture. Homogénéité : On vérifie que les intensités trouvées sont bien homogènes. Ici, il s’agit d’une somme de tensions sur une résistance : les relations sont donc bien homogènes.
Interprétation physique : On porte notre attention sur les puissances.
Quand \(U_2\) est négative, les deux sources de tensions tendent à faire circuler les électrons dans le même sens. Il n’y a pas de compétition et les deux fonctionnements en générateur
Quand \(U_2\) est positive, il y a compétition. Si \(U_2\) est trop faible (ici inférieure à \(U_1\)), il va fonctionner en récepteur.
En augmentant, il devient assez puissant pour fonctionner en générateur mais \(U_1\) étant encore important, il fonctionne aussi en générateur. Les deux dipôles alimentant alors les deux résistances.
En augmentant encore, \(U_2\) devient suffisamment important pour faire fonctionner \(D_2\) en récepteur.
