Caractéristiques d’un système d’ordre 2

Système d’ordre 2: Forme canonique

Important

Forme canonique des systèmes d’ordre 2

L’équation différentielle qui régit l’évolution d’un système d’ordre 2 peut se mettre une des formes suivantes:

(13)\[\begin{align} \frac{\rm{d^2}X}{\rm{dt^2}}(t) + \frac{\omega_0}{Q} \frac{\rm{d}X}{\rm{dt}}(t) + \omega_0^2 X(t) = F(t)\\ \frac{\rm{d^2}X}{\rm{dt^2}}(t) + 2 \xi \omega_0 \frac{\rm{d}X}{\rm{dt}}(t) + \omega_0^2 X(t) = F(t) \end{align}\]

On appelle

• \(Q\): le facteur de qualité du système

• \(\xi\): le coefficient d’amortissement du système

• \(\omega_0\): la pulsation propre du système

Relation entre les paramètres

Il est conseillé de s’entraîner à exprimer les paramètres précédents en fonction de \(\omega_0\) et Q (ou \(\omega_0\) et \(\xi\)).

Important

Type de régimes

La forme mathématique correspondant à la solution dépend de la valeur du facteur de qualité Q (ou du coefficient d’amortissement \(\xi\)) car ce dernier influe sur la valeur du discriminant de l’équation caractéristique \(\Delta\). A chaque expression différente correspond un type de régime:

	\(\Delta\)	Q	\(\xi\)	Forme ESSM
Régime apériodique	> 0	< 1/2	> 1	\(A \exp{r_1 t} + B \exp{r_2 t}\)
Régime critique	= 0	= 1/2	= 1	\(\exp{r_0 t} \left ( A t + B\right )\)
Régime pseudo-périodique	< 0	> 1/2	< 1	\(\exp{\lambda t} \left ( A \cos(\Omega t ) + B \sin(\Omega t ) \right )\)

On rappelle que :

• \(r_1\) et \(r_2\) sont les solutions de l’équation caractéristiques

• \(r_0\) est la solution double lorsque le discriminant est nul

• \(\lambda\) et \(\Omega\) sont respectivement la partie réelle de \(r_1\) et \(r_2\) et la partie imaginaire (en valeur absolue) de \(r_1\) et \(r_2\) lorsque le discriminant est négatif. On appelle \(\Omega\) la pseudo-pulsation du système.

Différents régimes de fonctionnement

Régime apériodique

Solution de l’équation homogène
On rappelle que la solution de l’équation homogène dans le cas où \(\Delta > 0\), c’est-à-dire \(Q < 1/2\) (ou \(\xi > 1\) est:

\[ X(t) = A \exp^{r_1 t} + B \exp^{r_2 t} \]

avec:

\[\begin{align*} r_1 = - \frac{\omega_0}{2Q} + \sqrt{\frac{\omega_0^2}{4Q^2} - \omega_0^2}\\ r_2 = - \frac{\omega_0}{2Q} - \sqrt{\frac{\omega_0^2}{4Q^2} - \omega_0^2} \end{align*}\]

On pourrait montrer (HP) qu’une telle expression ne peut avoir qu’un seul extremum local (ou 0).

Analyse des expressions
Remarquons que dans le cas où les coefficients sont positifs, les deux racines sont négatives: on retrouve le principe de stabilité du système.

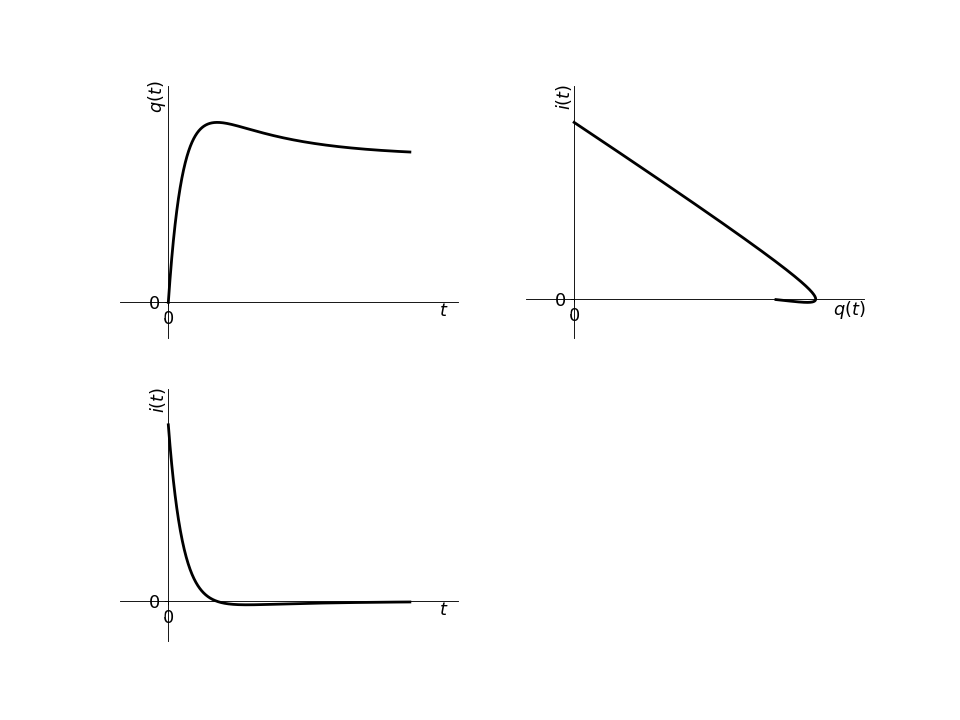
Tracés temporels et portrait de phase

Régime critique

Solution de l’équation homogène
On rappelle que la solution de l’équation homogène dans le cas où \(\Delta = 0\), c’est-à-dire \(Q = 1/2\) (ou \(\xi = 1\) est:

\[ X(t) = \exp^{r_0 t} \left ( At + B\right) \]

avec:

\[ r_0 = - \frac{\omega_0}{2Q} = - \omega_0 \]

On pourrait montrer (HP) qu’une telle expression ne peut avoir qu’un seul extremum local (ou 0).

Analyse des expressions
Remarquons que dans le cas où les coefficients sont positifs, la racine double est négative: on retrouve le principe de stabilité du système.

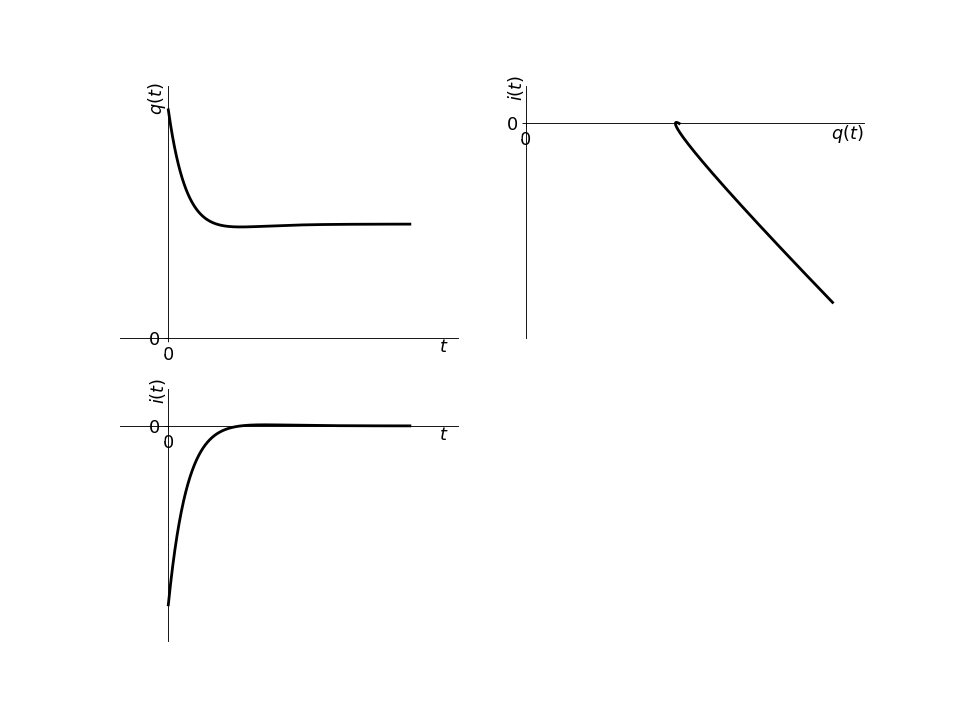
Tracés temporels et portrait de phase

Remarquons qu’il y a beaucoup de similarités avec le régime apériodique en terme de tracé. Pris séparément, on ne peut pas savoir si un tel tracé vient d’un régime apériodique ou critique.

Nous verrons en activité un moyen de comparer les deux tracés (quand on a les deux).

Régime pseudo-périodique

Solution analytique

Les signaux étant réels, on n’utilise pas la forme complexe de la solution.

Solution de l’équation homogène
On rappelle que la solution de l’équation homogène dans le cas où \(\Delta < 0\), c’est-à-dire \(Q > 1/2\) (ou \(\xi < 1\) est:

\[\begin{align*} X(t) &= \exp^{-\lambda t}\left( A \sin{\Omega t} + B \cos{\Omega t}\right)\\ &= \exp^{-\lambda t}\left( C \sin{(\Omega t + \phi)} \right)\\ \end{align*}\]

avec:

\[\begin{align*} \lambda &= Re(r_{1,2}) = - \frac{\omega_0}{2Q}\\ \Omega &= \left\vert Im(r_{1,2}) \right\vert = \omega_0 \sqrt{1 - \frac{1}{4Q^2}} \end{align*}\]

Analyse des expressions
Remarquons que dans le cas où les coefficients sont positifs, le coefficient de l’exponentielle (issue de la partie réelle des racines) est négatif: on retrouve le principe de stabilité du système.

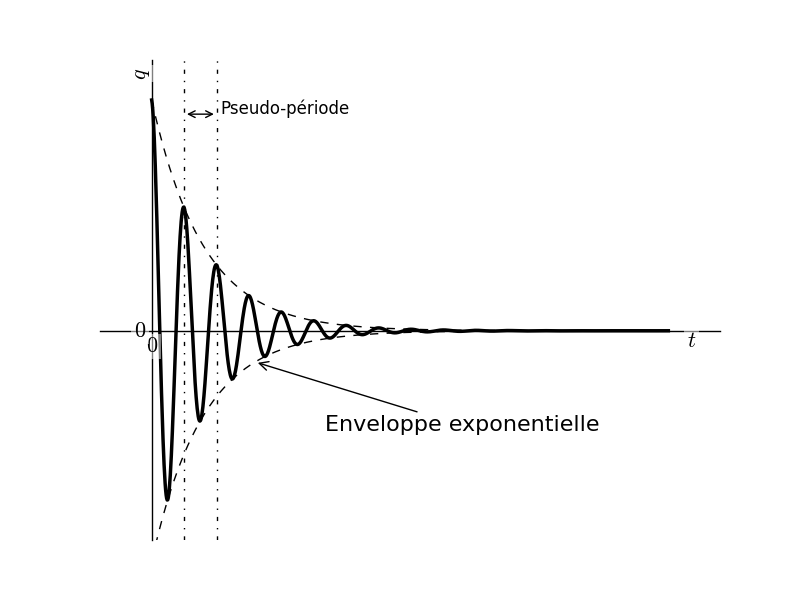
Tracé temporelle

Pseudo-période et période propre

Il ne faut pas confondre la pseudo-période qu’on peut obtenir d’un tracé temporel et qui est reliée à la pseudo-pulsation et la période propre, reliée à la pulsation propre et qui n’apparaît pas directement dans les tracés temporel.

La période propre, comme la pulsation propre est un élément caractéristique issu de la forme canonique de l’équation : \(T_0 = \frac{2\pi}{\omega_0}\).

A l’inverse, la pseudo-période n’intervient pas dans la mise sous forme canonique mais apparaît dans les mesures expérimentales qu’on peut être amené à faire sur un système en régime pseudo-périodique.

Pour relier les deux, il faut le facteur de qualité.

Tracé temporelle
L’expression \(X(t) = \exp^{-\lambda t}\left( D \sin^{\Omega t + \phi} \right)\) permet de dessiner facilement l’évolution de X(t) en régime pseudo-périodique.

En effet, on remarque qu’il s’agit d’un signal sinsoïdal de pulsation \(\Omega\) ou plutôt pseudo-sinusoïdal car l’amplitude décroît de manière exponentielle.

Pour représenter X(t), il faut d’abord représenter son enveloppe exponentielle: \(D \exp^{- \frac{\omega_0 t}{2Q}}\). On représente alors à l’intérieur de l’enveloppe un sinusoïde (dont l’amplitude décroît) de pseudo-période \(T = \frac{2 \pi}{\Omega}\).

Régime pseudo-périodique: Décrément logarithmique

Amortissement et décroissance exponentielle

Dans le cas d’un régime pseudo-périodique, l’amplitude du pseudo-sinusoïde décroît de manière exponentielle. C’est la vitesse de décroissance qui va déterminer dans ce régime la force de l’amortissement.

Comme cette décroissance est exponentielle, nous utilisons un indicateur particulier pour quantifier l’amortissement.

Important

Décrément logarithmique.

Pour un régime pseudo-périodique de pseudo-période T, on définit le décrément logarithmique \(\delta\) par:

\[ \delta = \ln \left( \frac{u(t) - u(t=+\infty)}{u(t+T) - u(t=+\infty)}\right) \]

Interprétation

On calcule l’écart à la valeur finale à deux instants t et t+T (ce second écart est plus faible pour un système stable). En faisant le rapport, on obtient un nombre d’autant plus grand que l’amortissement est fort. Le décrément est donc une mesure l’amortissement en régime pseudo-périodique.

Le fait que la décroissance soit exponentielle explique que l’on prenne le logarithmique du rapport. Nous allons voir que cela simplifie l’expression.

Analyse

On peut analyser l’expression précédente en remarquant que plus Q augmente, plus \(\delta\) diminue. Il vient que en régime pseudo-périodique, plus Q est grand, plus l’amortissement est faible. On retrouve d’ailleurs ce principe avec le temps caractéristique qu’on a calculer précédemment.

Important

Relation entre le décrément logarithmique et le facteur de qualité On peut montrer que (‘sentraîner à le faire - correction en ligne):

$\( \delta = \frac{2\pi}{\sqrt{4Q^2 - 1}} \)$\end{basic}

Démonstration

\[\begin{align*} \delta &= \ln \left( \frac{u(t) - u(t=+\infty)}{u(t+T) - u(t=+\infty)}\right)\\ &= \ln \left( \frac{e^{-\lambda t} \left(C \cos{\Omega t + \varphi} \right)}{e^{-\lambda (t+T)} \left(C \cos{\Omega (t + T) + \varphi} \right)}\right)\\ &= \ln \left( \frac{e^{-\lambda t} \left(\cos{\Omega t + \varphi} \right)}{e^{-\lambda (t+T)} \left(\cos{\Omega t + \Omega T + \varphi} \right)}\right)\\ &= \ln \left( \frac{e^{-\lambda t} \left(\cos{\Omega t + \varphi} \right)}{e^{-\lambda (t+T)} \left(\cos{\Omega t + 2\pi + \varphi} \right)}\right)\\ \end{align*}\]

soit :

\[\begin{align*} \delta &= \ln \left( \frac{e^{-\lambda t} \left(\cos{\Omega t + \varphi} \right)}{e^{-\lambda (t+T)} \left(\cos{\Omega t + \varphi} \right)}\right)\\ &= \ln \left( \frac{e^{-\lambda t}}{e^{-\lambda (t+T)}}\right)\\ &= \ln \left( e^{\lambda T}\right)\\ &= \lambda T\\ \end{align*}\]

soit :

\[\begin{align*} \delta &= \frac{\omega_0}{2Q} \frac{2\pi}{\omega_0 \sqrt{1 - \frac{1}{4Q^2}}}\\ &= \frac{2\pi}{2Q\sqrt{1 - \frac{1}{4Q^2}}}\\ &= \frac{2\pi}{\sqrt{4Q^2 - 1}} \end{align*}\]

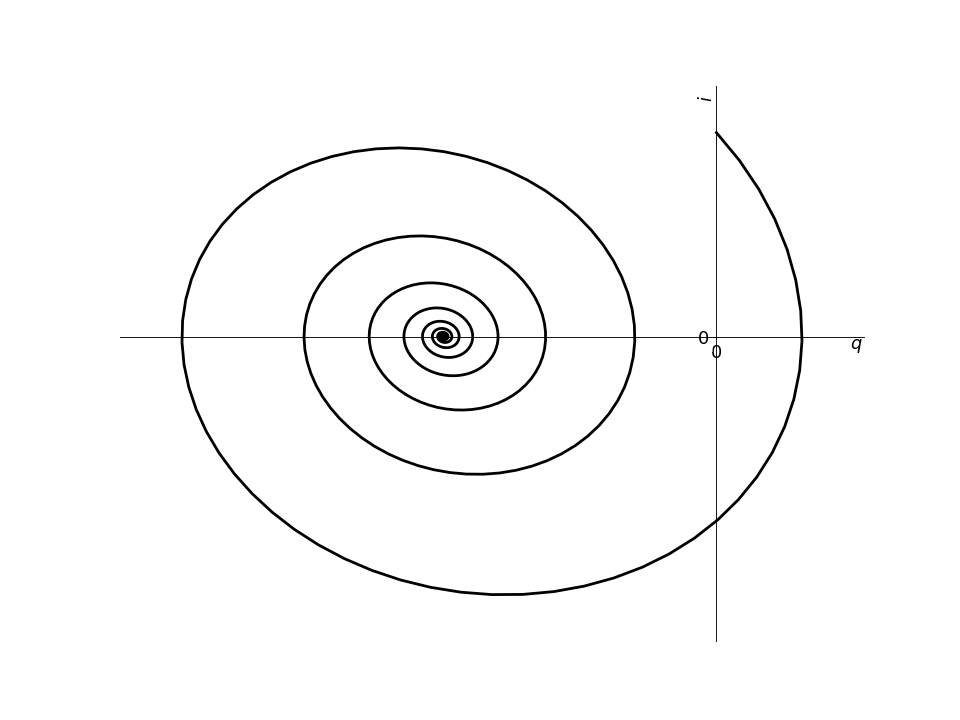
Portrait de phase (en ligne)

Allure du portrait de phase

Le portrait de phase en régime pseudo-périodique est une spirale elliptique convergeant vers le régime forcé.

Si l’on représente la dérivée \(\dot X(t)\) en fonction de la fonction X(t), la spirale tourne dans le sens horaire.