Exemple : Etude d’un système d’ordre 1
Contents
Exemple : Etude d’un système d’ordre 1#
On se propose de retrouver les caractéristiques précédentes sur l’exemple suivant:
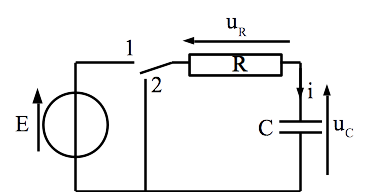
L’interrupteur étant en position 1 depuis un temps long, il bascule à t=0 en position 2.
Mise en équation
Déterminer l’équation différentielle qui régit l’évolution de \(u_C\) pour \(t>0\).
Correction
La loi des mailles s’écrit: \(u_R + u_C = 0 = R i + u_C\).
En utilisant l’équation d’évolution du condensateur, il vient:
(14)#\[\begin{equation} \frac{\rm{d}u_C}{\rm{dt}}(t) + \frac{1}{RC} u_C(t) = 0 \end{equation}\]On a donc \(\tau = RC\)
Evolution temporelle
Déterminer \(u_C(t)\) et \(i(t)\) pour \(t>0\) et tracé leur allure temporelle.
Correction - uC(t)
La solution générale est donc \(A e^{-t/\tau}\) avec \(\tau = RC\).
Le second membre étant nul, il n’y a pas de solution particulière à ajouter.
Il faut déterminer la condition initiale (système d’ordre 1 donc il n’y a qu’une condition initiale).
On peut étudier le système à \(t=0^-\) en considérant qu’on est en régime forcé. La seule grandeur continue est la tension aux bornes du condensateur. On va déterminer sa valeur.
Le condensateur étant assmilable à un interrupteur ouvert, l’intensite i est nulle donc la tension aux bornes de la résistance aussi. Il vient \(u_C(t=0^-) = E\)
Par continuité \(u_C(t=0^+) = E\).
La condition initiale permet d’écrire A = E soit:
(15)#\[\begin{equation} u_C(t) = E \exp^{-t/\tau} \end{equation}\]
Correction - i(t)
Pas besoin de tout réétudier. Il suffit d’utiliser la relation \(i = C \frac{\rm{d}u_C}{\rm{dt}}\):
(16)#\[\begin{equation} i(t) = -\frac{E}{R} \exp^{-t/\tau} \end{equation}\]
Allures temporelles
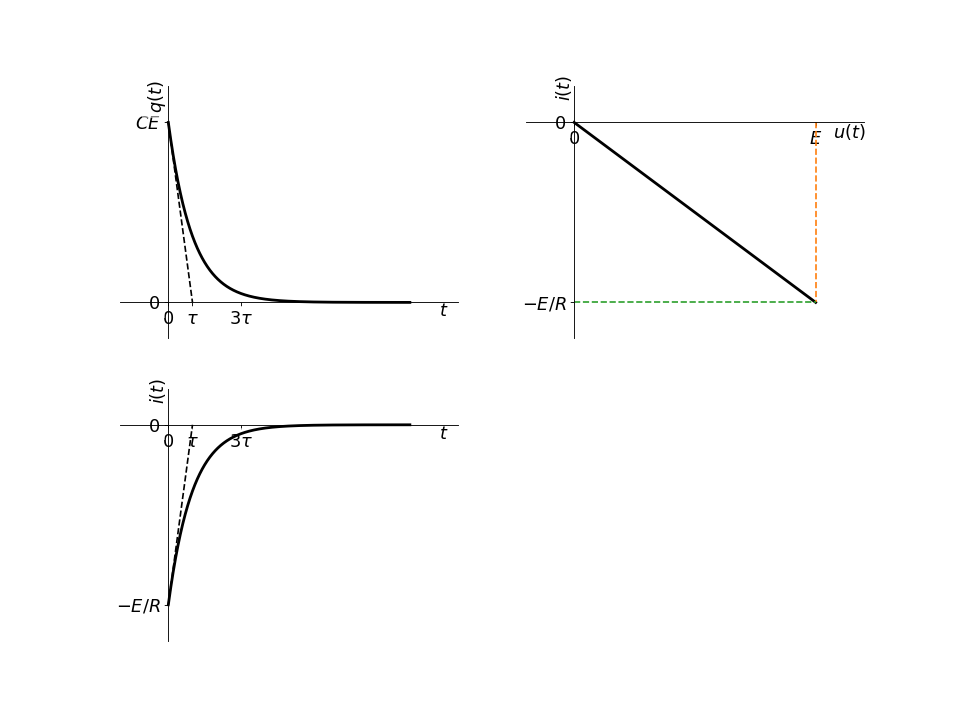
On a représenté la charge et non la tension mais on rappelle que les deux sont proportionnelles.
Etude énergétique#
Bilan de puissance et d’énergie
Réaliser un bilan de puissance du circuit RC précédent.
Réaliser un bilan d’énergie du circuit RC précédent entre \(t=0\) et \(t=+\infty\).
Bilan de puissance
Faire un bilan de puisance revient à trouver une relations entre les différentes puissance mise en jeu à un instant. Il suffit en général de partir d’une des équations (loi des noeuds ou des mailles).
Partons de la loi des mailles: \(u_R + u_C = 0\) et multiplions là par i. On obtient des puissances reçues: \(p_J(t) + p_C(t) = 0\) avec \(p_J(t)\) la puissance perdue par effet Joule dans la résistance et \(p_C(t)\) la puissance reçue par le condensateur.
La puissance dissipée par effet Joule dans R est entièrement fournie par C.
D’ailleurs, par le calcul, remarquons que \(p_C(t) = - \frac{E^2}{R} \exp^{-\frac{2t}{RC}} < 0\) donc le condensateur fournie de la puissance durant toute l’expérience. Cette puissance fournie \(-p_C(t)\) égale la puissance dissipée à chaque instant dans la résistance \(p_J(t)\)
Bilan d’énergie
Il s’agit de calculer les énergies reçue/fournie par chaque dipôle pour les comparer.
Energie fournie par le condensateur
On peut calculer l’énergie fournie par le condensateur de deux manières: en intégrant la puissance qu’il fournit ou en utilisant la variation d’énergie stockée.S’il faut savoir faire les deux dans un cas simple comme un circuit d’ordre 1, il vaut mieux privilégier l’utilisation de l’énergie stockée si on a le choix. Ici, l’énergie fournie par le condensateur est:
(17)#\[\begin{equation} \Delta E_C = E_L(0) - E_L(t=+\infty) = \frac{1}{2}C u_C(t=0)^2 - \frac{1}{2}C u_C(t=+\infty)^2 = \frac{C E^2}{2} \end{equation}\]
Energie dissipée par effet Joule dans R
Pour la résistance, on n’a pas le choix, l’énergie dissipée ne peut se calculer qu’en intégrant la puissance reçue soit:(18)#\[\begin{equation} E_J = \int_{t=0}^{t=+\infty} \frac{u_R^2(t)}{R} dt = \int_{t=0}^{t=+\infty} \frac{E^2}{R} \exp^{-\frac{2t}{RC}} dt = \frac{CE^2}{2} \end{equation}\]
Bilan énergétique
On observe que l’énergie fournie par le condensateur est entièrement dissipée par effet Joule dans la résistance, ce qui est logique puisque cette correspondance était déjà valable à chaque instant.
Application à la réponse indicielle d’un circuit RC#
Nous allons étudier la réponse indicielle qui permettra de rappeler la méthode pour la recherche de la solution particulière. Il est conseillé de s’entraîner à faire l’exercice avant de regarder les réponses.
Exercice
On considère toujours le circuit RC mais après un temps long en position 2, l’interrupteur bascule à t=0 en position 1.
Déterminer avec peu de calculs l’état final de \(u_C(t)\)
Déterminer l’équation différentielle qui régit l’évolution de \(u_C(t)\) puis déterminer \(u_C(t)\).
En déduire i(t).
Réaliser un bilan de puissance et un bilan énergétique sur l’ensemble du circuit.
Correction
Q1. Nouveau régime forcé
On peut considérer le système comme stable et le régime forcé sera indépendant du temps car E est constant.Le condensateur se comporte alors comme un interrupteur ouvert et i=0. Il vient \(u_C = E\)
Q2. Mise en équation
Cette fois la loi des mailles s’écrit: \(E - R i(t) - u_C(t) = 0\). On utilise à nouveau la relation tension-intensité du condensateur, il vient:(19)#\[\begin{equation} \frac{\rm{d}u_C}{\rm{dt}}(t) + \frac{1}{RC} u_C(t) = \frac{E}{RC} \end{equation}\]On doit déterminer les conditions initiales. Dans le régime forcé indépendant du temps avant t=0, on cherche la grandeur continue, ici la tension aux bornes du condensateur. Le condensateur se comporte comme un interrupteur ouvert donc l’intensité est nulle et donc \(u_C(t=0^-) = u_R(t=0^-) = 0\)
Par continuité \(u_C(t=0^+) = 0\)
La solution générale ESSM est toujours \(A \exp^{-t/RC}\)
On cherche une solution particulière constante \(U_0\). En l’introduisant dans l’équation différentielle, il vient \(0 + \frac{U_0}{RC} = \frac{E}{RC}\) soit \(U_0 = E\)
La solution est donc: \(A \exp^{-t/RC} + E\)
On utilise la condition initiale qui donne A = -E donc:
(20)#\[\begin{equation} u_C(t) = E (1 - \exp^{-t/\tau}) \end{equation}\]Q3. Intensité
Il suffit de dériver et de multiplier par C:(21)#\[\begin{equation} i(t) = \frac{E}{R} \exp^{-t/\tau} \end{equation}\]
Q4. Etude énergétique
Bilan de puissance: la loi des mailles \(E = u_R + u_C\) multiplié par i donne: \(P_E = P_J + P_C\). On pourra remarquer que cette fois \(P_C > 0\)On observe que la puissance fournie par le générateur va en partie est stockée par le condensateur et en partie dissipée par la résistance.
Bilan énergétique:
On commence par l’énergie fournie par le générateur:
(22)#\[\begin{equation} E_E= \int_{t=0}^{t=+\infty} Ei(t) dt = \int_{t=0}^{t=+\infty} \frac{E^2}{R} \exp^{-\frac{t}{RC}} dt = CE^2 \end{equation}\]Ensuite l’énergie dissipée par la résistance:
(23)#\[\begin{equation} E_J = \int_{t=0}^{t=+\infty} R i^2(t) dt = \int_{t=0}^{t=+\infty} \frac{E^2}{R} \exp^{-\frac{2t}{RC}} dt = \frac{CE^2}{2} \end{equation}\]Enfin l’énergie stockée par le condensateur:
(24)#\[\begin{equation} \Delta E_C = E_C(t=+\infty) - E_C(t=0) = \frac{1}{2}C u_C(t=\infty)^2 - \frac{1}{2}C u_C(t=0)^2 = \frac{C E^2}{2} \end{equation}\]
