Mise en cascade des filtres (en ligne)

Mise en cascade. Généralités

Rappel : Hypothèse d’étude des filtres

On rappelle qu’on étudie toujours les filtres en supposant que l’intensité de sortie est nulle. Ce n’est pas forcément vrai si la sortie est branchée sur un dispositif résistif ou si l’on place deux filtres en cascade.

Une conséquence est que si l’on met deux filtres en cascade, les calculs des fonctions de transfert des filtres séparés ne sont a priori plus valables.

Exemple

• Si l’on considère un filtre RC passe-bas, la fonction de transfert est \(\underline{H} = \frac{1}{1 + j RC \omega}\).

  • Si l’on place à la suite deux filtre RC passe-bas identique, la fonction de transfert ne sera pas \(\underline{H}^2\).

Quadripôle et impédances

Modélisation d’un quadripôle

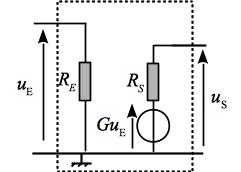
Un quadripôle fait le lien entre un premier et une second circuit. Du point du vue du premier circuit, il est assimilable à une résistance (résistance d’entrée). Du point de vue du circuit de sortie, il est assmilable à un modèle de Thévenin de fem \(\underline{H}\underline{e}\) et de résistance \(R_S\) appelée résistance de sortie.

En toute rigueur, les résistances sont parfois remplacées par des impédances pour affiner le modèle. En général, une modélisation en terme de résistance suffira.

Exemple

• Considérons à nouveau un filtre RC passe-bas. Si l’on annule l’intensité de sortie, l’impédance équivalente présentée au circuit d’entrée est \(\underline{Z_e} = R + \frac{1}{jC \omega}\).

• Pour le circuit de sortie, la fem équivalente est \(\frac{\underline{e}}{1 + j RC \omega}\) et d’impédance de sortie \(\underline{Z_s} = \frac{R}{1 + j RC \omega}\)

Mise en cascade des filtre et impédances

Important

Mise en cascade

• Deux filtres mis en cascade auront des comportement indépendants si l’impédance de sortie du premier est très faible devant l’impédance d’entrée du second.

• Dans ces conditions, on peut étudier les deux filtres séparément et obtenir la fonction de transfert complète par multiplication.

Démonstration

La principale problématique est de pouvoir utiliser la fonction de transfert du premier filtre. Pour celà, il faut que la chute de tension occasionnée par la résistance de sortie du premier filtre soit nulle (ou quasi-nulle). Un calcul de cette chute de tension (par un pont diviseur de tension par exemple) donne \(\underline{i} = \frac{R_{s1}\underline{H}\underline{e}}{R_{s1} + R_{e2}}\) avec \(R_{s1}\) la résistance de sortie du premier filtre et \(R_{e2}\) la résistance d’entrée du second filtre. La chute de tension sera nulle si \(R_{s1} \ll R_{e2}\)

Mise en pratique: utilisation d’un suiveur.

Lorsqu’on veut mettre en cascade deux filtres qui ne vérifient la condition précédente, on va intercaler un suiveur. Un suiveur est un montage de gain unitaire (s = e) mais qui possède une impédance d’entrée très grande et une impédance de sortie très faible. Celà permet de réaliser la condition de mise en cascade.

Rappel : Un suiveur est un montage simple utilisant un amplificateur linéaire intégré.