Activités : Typologie des filtres#

Pour chaque filtre, démontrer les caractéristiques - qui sont aussi à connaitre par coeur - à partir de la forme canonique.

Filtre passe-bas d’ordre 1#

Important

Forme canonique

Un filtre passe bas d’ordre 1 peut se mettre sous la forme:

\[\begin{align*} \underline{H} = \frac{H_0}{1 + j x} \end{align*}\]

avec la pulsation réduite \(x = \frac{\omega}{\omega_0}\) et la pulsation propre \(\omega_0\).

Caractéristiques
Les caractéristiques que vous devez savoir calculer/prouver sont:

  • ses limites haute et basse fréquence qui permettent de reconnaître un tel filtre: la limite HF est nulle et la limite BF est non nulle.

  • l’expression de son gain réel, de son gain en décibel et de sa phase

  • le gain réel est strictement décroissant.

  • SI \(H_0 > 0\): La phase passe de 0 à \(-\pi / 2\) et elle vaut \(-\pi/4\) à la pulsation propre.

  • La pulsation de coupure est égale à la pulsation propre.

  • Le diagramme de Bode admet une asymptote horizontale à basse fréquence et une asymptote oblique de pente \(-20 dB/decade\) à haute fréquence.

Diagramme de Bode
On retrouve les caractéristiques précédentes sur le diagramme de Bode.

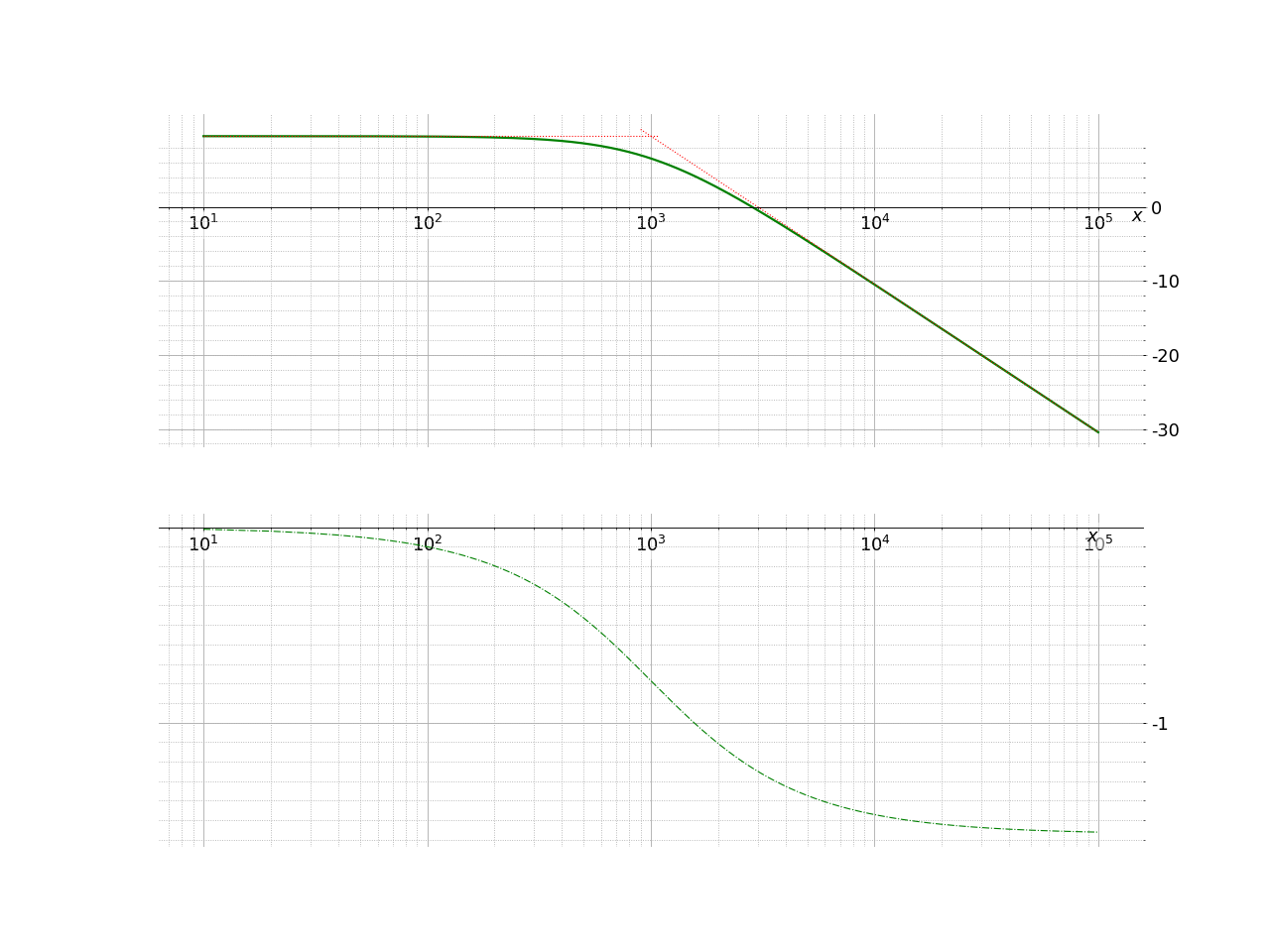
../_images/filtre_cano_o1_pbas.png

Fig. 18 Filtre passe-bas d’ordre 1#

Filtre passe-haut d’ordre 1#

Important

Forme canonique

Un filtre passe haut d’ordre 1 peut se mettre sous la forme:

\[\begin{align*} \underline{H} = \frac{jH_0 x}{1 + j x} \end{align*}\]

avec la pulsation réduite \(x = \frac{\omega}{\omega_0}\) et la pulsation propre \(\omega_0\).

Caractéristiques
Les caractéristiques que vous devez savoir calculer/prouver sont:

  • ses limites haute et basse fréquence qui permettent de reconnaître un tel filtre: la limite HF est non nulle et la limite BF est nulle.

  • l’expression de son gain réel, de son gain en décibel et de sa phase

  • le gain réel est strictement croissant.

  • la pulsation de coupure est égale à la pulsation propre.

  • Si \(H_1 > 0\): La phase passe de \(\pi / 2\) à 0 et elle vaut \(\pi/4\) à la pulsation propre.

  • Le diagramme de Bode admet une asymptote horizontale à haute fréquence et une asymptote oblique de pente \(20 dB/decade\) à basse fréquence.

Diagramme de Bode
On retrouve les caractéristiques précédentes sur le diagramme de Bode.

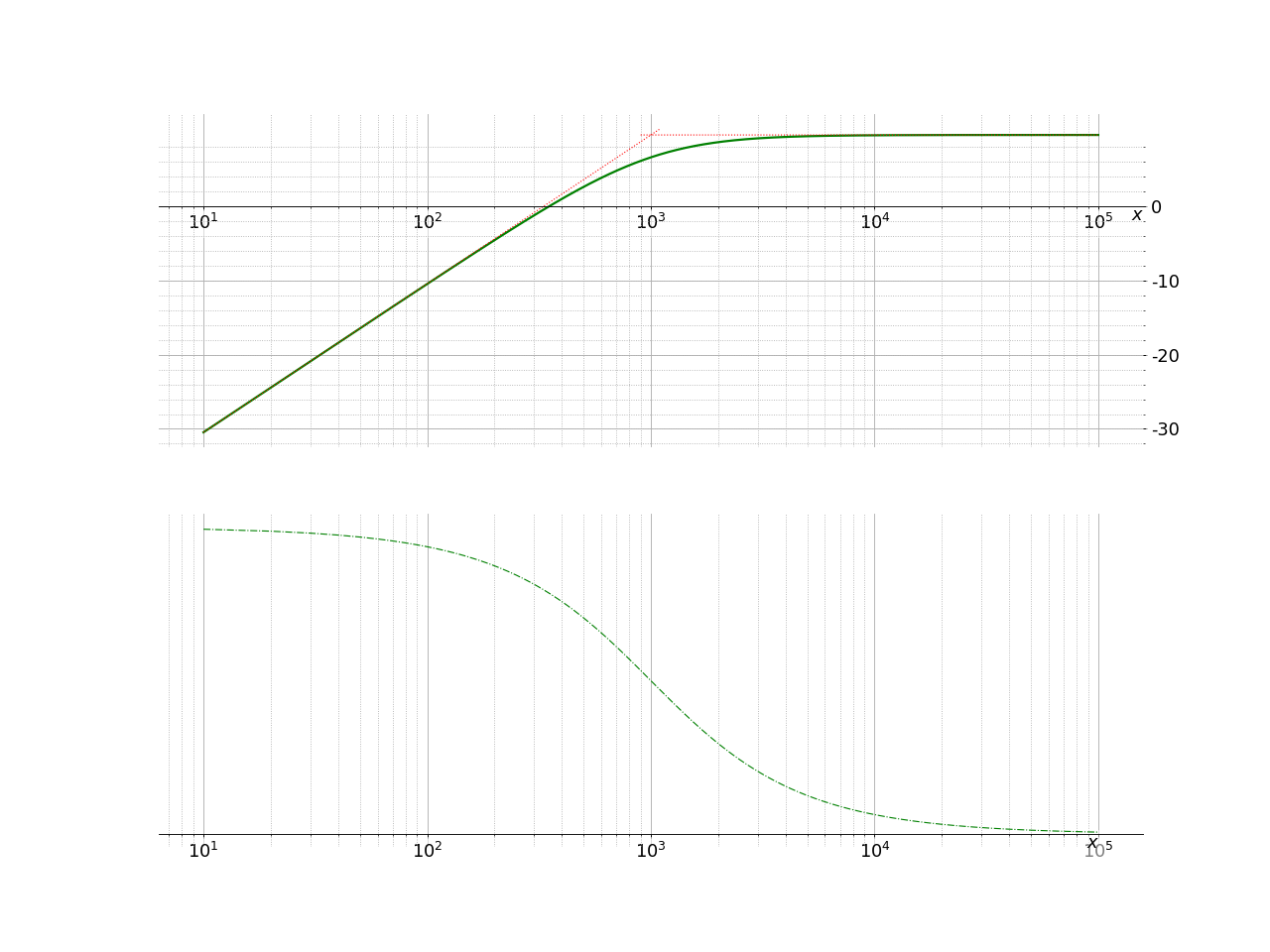
../_images/filtre_cano_o1_phaut.png

Fig. 19 Filtre passe-haut d’ordre 1#

Filtre passe-bas d’ordre 2#

Important

Forme canonique

Un filtre passe bas d’ordre 2 peut se mettre sous la forme:

\[\begin{align*} \underline{H} = \frac{H_0}{1 - x^2 + j \frac{x}{Q}} \end{align*}\]

avec la pulsation réduite \(x = \frac{\omega}{\omega_0}\), le facteur de qualité Q et la pulsation propre \(\omega_0\).

Caractéristiques
Les caractéristiques que vous devez savoir calculer/prouver sont:

  • ses limites haute et basse fréquence qui permettent de reconnaître un tel filtre: la limite HF est nulle et la limite BF est non nulle.

  • l’expression de son gain réel, de son gain en décibel et de sa phase

  • l’existence d’une résonance conditionnée à un facteur de qualité tel que \(Q > \frac{1}{\sqrt{2}}\). La fréquence de résonance dépend du facteur de qualité. Elle tend vers 0 quand Q décroit et vers la pulsation propre quand Q augmente.

  • La phase passe de 0 à \(-\pi\) (ou de \(\pi\) à 0 si \(H_0 < 0\)). Elle vaut \(-\pi/2\) (ou \(\pi/2\)) à la pulsation propre.

  • Le diagramme de Bode admet une asymptote horizontale à basse fréquence et une asymptote oblique de pente \(-40 dB/decade\) à haute fréquence.

[Diagramme de Bode()]
On retrouve les caractéristiques précédentes sur le diagramme de Bode. Plusieurs tracés sont représentés pour différentes valeurs de Q.

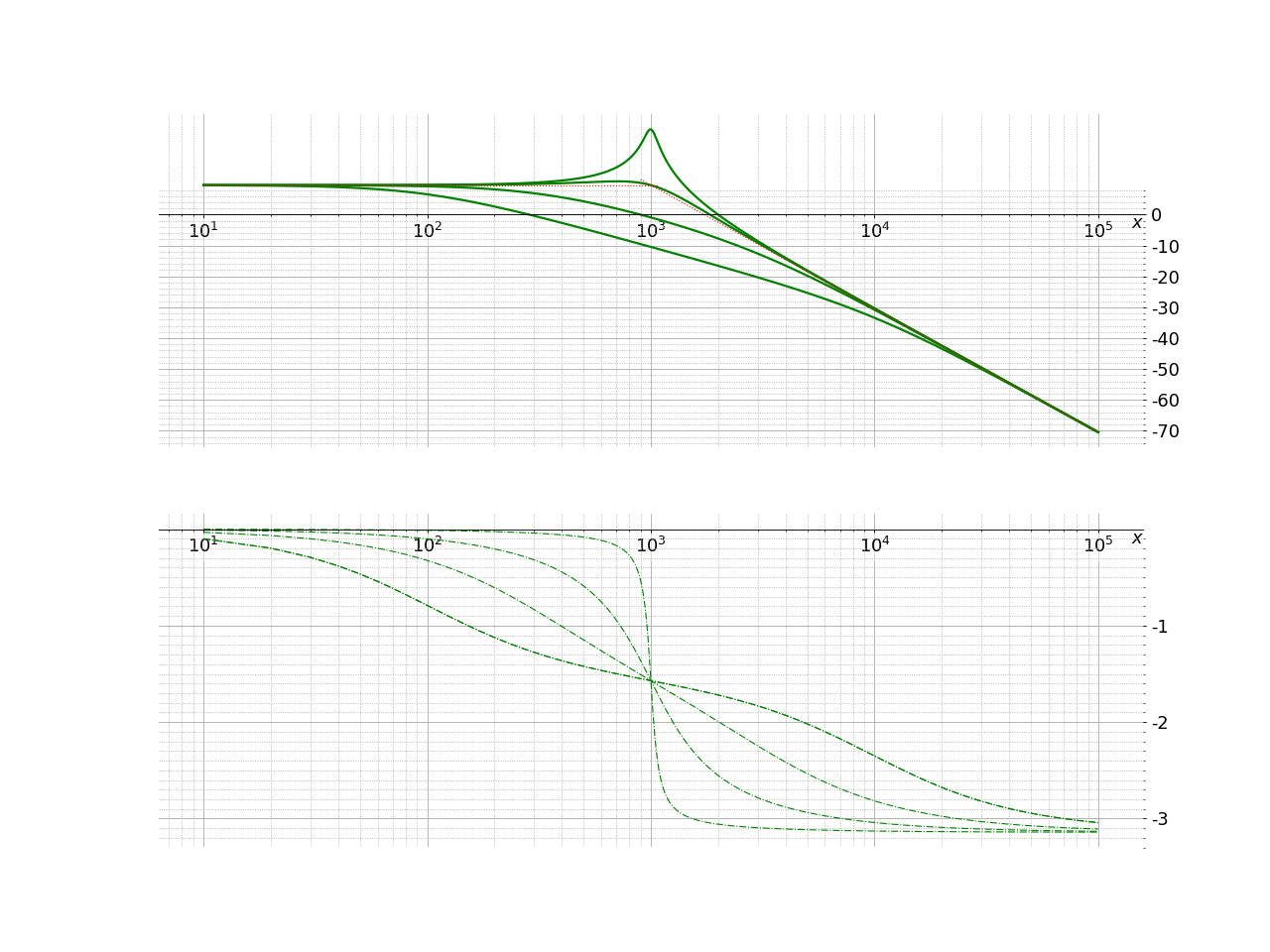
../_images/filtre_cano_o2_pbas.png

Fig. 20 Filtre passe-bas d’ordre 2#

Filtre passe-haut d’ordre 2#

Important

Forme canonique

Un filtre passe haut d’ordre 2 peut se mettre sous la forme:

\[\begin{align*} \underline{H} = \frac{- H_1 x^2}{1 - x^2 + j \frac{x}{Q}} \end{align*}\]

avec la pulsation réduite \(x = \frac{\omega}{\omega_0}\), le facteur de qualité Q et la pulsation propre \(\omega_0\).

Caractéristiques
Les caractéristiques que vous devez savoir calculer/prouver sont:

  • ses limites haute et basse fréquence qui permettent de reconnaître un tel filtre: la limite HF est non nulle et la limite BF est nulle.

  • l’expression de son gain réel, de son gain en décibel et de sa phase

  • l’existence d’une résonance conditionnée à un facteur de qualité tel que \(Q > \frac{1}{\sqrt{2}}\). La fréquence de résonance dépend du facteur de qualité. Elle tend vers l’infini quand Q décroit et vers la pulsation propre quand Q augmente.

  • La phase passe de \(\pi\) à 0 (ou de 0 à \(-\pi\) si \(H_1 < 0\)). Elle vaut \(\pi/2\) (ou \(- \pi/2\)) à la pulsation propre.

  • Le diagramme de Bode admet une asymptote horizontale à haute fréquence et une asymptote oblique de pente \(40 dB/decade\) à basse fréquence.

Diagramme de Bode
On retrouve les caractéristiques précédentes sur le diagramme de Bode. Plusieurs tracés sont représentés pour différentes valeurs de Q.

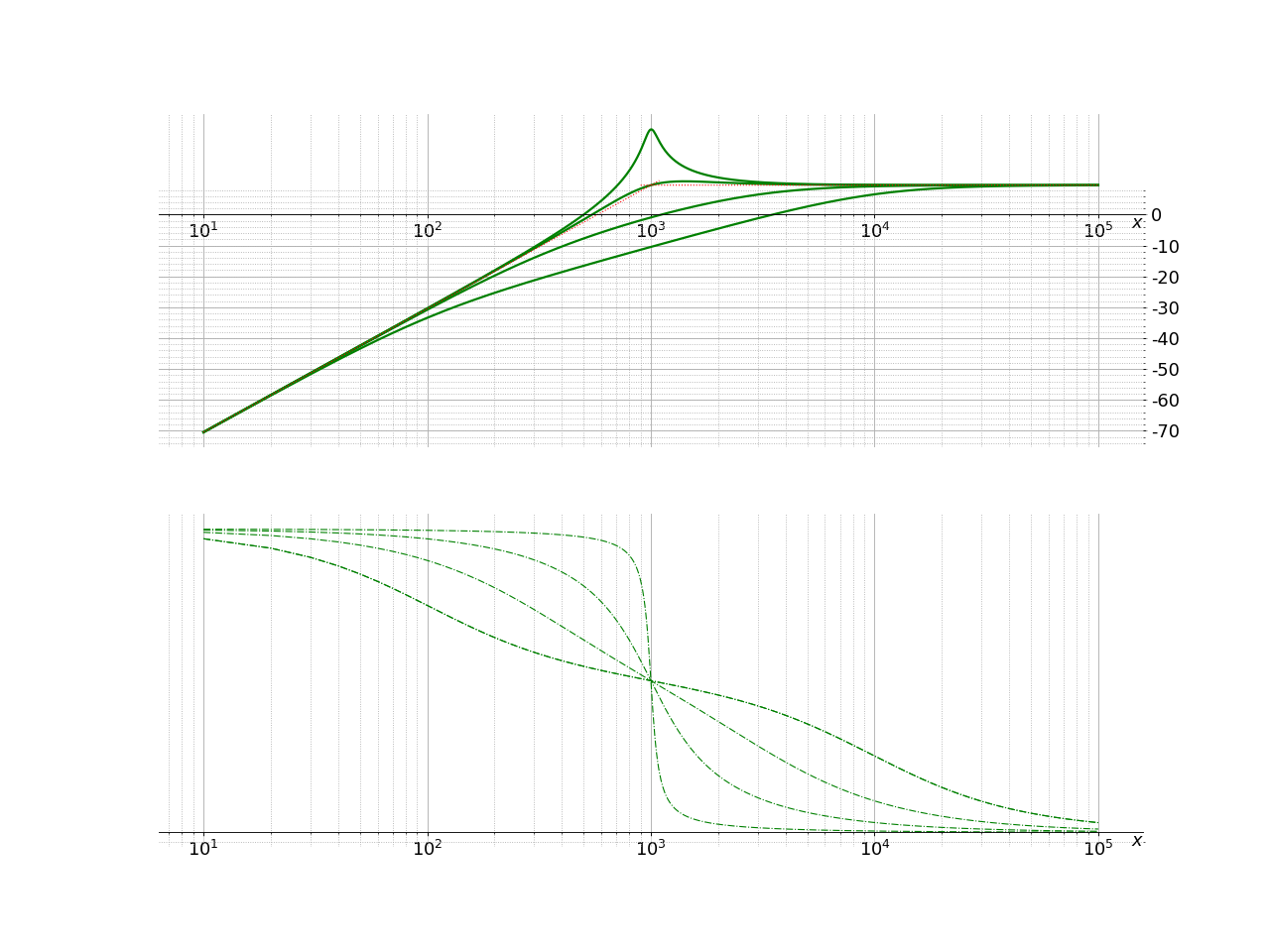
../_images/filtre_cano_o2_phaut.png

Fig. 21 Filtre passe-haut d’ordre 2#

Filtre passe-bande d’ordre 2#

Important

Forme canonique

Un filtre passe bande d’ordre 2 peut se mettre sous la forme:

\[\begin{align*} \underline{H}& = \frac{H_2}{1 + jQ \left(x - \frac{1}{x}\right)}\\ & = \frac{j H_2 \frac{x}{Q}}{1 - x^2 + j \frac{x}{Q}} \end{align*}\]

avec la pulsation réduite \(x = \frac{\omega}{\omega_0}\), le facteur de qualité Q et la pulsation propre \(\omega_0\).

Caractéristiques
Les caractéristiques que vous devez savoir calculer/prouver sont:

  • ses limites haute et basse fréquence qui permettent de reconnaître un tel filtre: la limite HF est nulle et la limite BF est nulle.

  • l’expression de son gain réel, de son gain en décibel et de sa phase

  • l’existence d’une résonance quelque soit la valeur du facteur de qualité. La fréquence de résonance est toujours la pulsation propre.

  • La bande passante possède une largeur \(\Delta \omega = \frac{\omega_0}{Q}\). Les pulsations de coupure sont symétriques sur un diagramme de Bode: \(\omega_{c1} \times \omega_{c2} = \omega_0^2\).

  • Si \(H_2 > 0\): La phase passe de \(\pi / 2\) à \(-\pi/2\) et elle vaut 0 à la pulsation propre, on dit que les signaux entrée et sortie sont en phase.

  • Le diagramme de Bode admet une asymptote oblique à basse fréquence de pente \(20 \rm{dB/decade}\) et une asymptote oblique de pente \(-20 dB/decade\) à haute fréquence.

Diagramme de Bode
On retrouve les caractéristiques précédentes sur le diagramme de Bode. Plusieurs tracés sont représentés pour différentes valeurs de Q (\(H_2\) et \(\omega_0\) étant fixés).

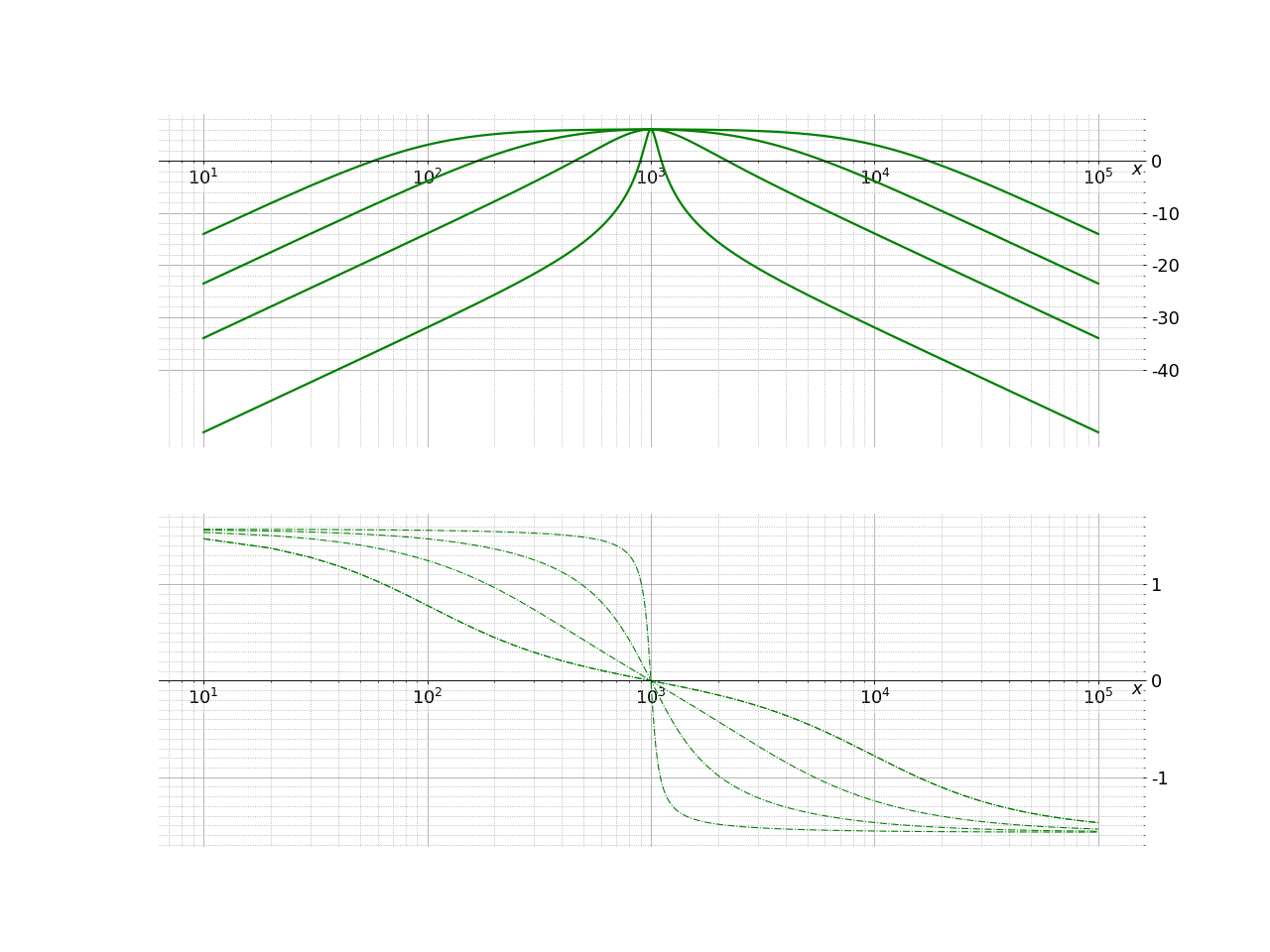
../_images/filtre_cano_o2_pbande.png

Fig. 22 Filtre passe-bande d’ordre 2#

Filtre coupe-bande d’ordre 2#

Important

Forme canonique

Un filtre coupe bande d’ordre 2 peut se mettre sous la forme:

\[\begin{align*} \underline{H}& = \frac{H_3 (1 - x^2)}{1 - x^2 + j \frac{x}{Q}} \end{align*}\]

avec la pulsation réduite \(x = \frac{\omega}{\omega_0}\), le facteur de qualité Q et la pulsation propre \(\omega_0\).

Caractéristiques
Les caractéristiques que vous devez savoir calculer/prouver sont:

  • ses limites haute et basse fréquence qui permettent de reconnaître un tel filtre: la limite HF et la limite BF sont égales et non nulles.

  • l’expression de son gain réel, de son gain en décibel et de sa phase

  • l’existence d’une anti-résonance: le gain s’annule à la pulsation propre.

  • La bande coupée (définie comme la bande de fréquence où le gain est inférieure au gain maximal divisé par \(\sqrt{2}\)) possède une largeur \(\Delta \omega = \frac{\omega_0}{Q}\). Les pulsations de coupure sont symétriques sur un diagramme de Bode: \(\omega_{c1} \times \omega_{c2} = \omega_0^2\).