Entrainement
Contents
Entrainement#
Etude fréquentielle#
Antirésonance
On considère un dipôle RLC série alimenté par une tension sinusoïdale. On s’intéresse à la tension u aux borne de l’ensemble L+C en régime sinusoïdal forcé.
Déterminer l’amplitude complexe de u puis son amplitude réelle. En déduire la valeur maximale de l’amplitude réelle \(u_{\max}\).
Montrer que l’amplitude s’annule pour une pulsation qu’on déterminera. On parle d’antirésonance.
On définit la bande coupée comme la bande de fréquence pour laquelle l’amplitude réelle \(u_m(\omega)\) soit telle que \(u_m(\omega) \leq \frac{u_{\max}}{\sqrt{2}}\). Préciser sa largeur.
Point utile pour cet exercice
\(\Longrightarrow\) Etude d’un circuit en RSF
\(\Longrightarrow\) Résonance et bande passante
Eléments de réponse (sans justification)
\(\underline{u} = \frac{1-x^2}{1 - x^2 + j \frac{x}{Q}}E\) avec \(x = \frac{\omega}{\omega_0}\), \(\omega_0 = \sqrt{\frac{1}{LC}}\) et \(Q = \frac{1}{R}\sqrt{\frac{L}{C}}\).
L’amplitude de u est maximale aux fréquences extrêmes et s’annule à la pulsation propre. La largeur de la bande coupée est \(\frac{\omega_0}{Q}\).
Etude d’une réponse#
Détection
On considère un circuit constitué d’une résistance R en série avec un condensateur C. L’ensemble est reliée à une source de tension \(e(t)\) fournissant une tension: \(e(t) = e_m \sin \omega_1 t \sin \omega_2 t\) avec \(\omega_1 = 1.01 \omega_2 = \frac{50}{RC}\).
Déterminer la tension aux bornes du condensateur en régime forcé. Simplifier l’expression par approximation en utilisant les ordres de grandeurs des pulsations mises en jeu.
Point utile pour cet exercice
\(\Longrightarrow\) Etude d’un circuit en RSF
\(\Longrightarrow\) Réponse d’un filtre linéaire
\(\Longrightarrow\) Manipulation des complexes
Eléments de réponse (sans justification)
\(u(t) = \frac{e_m}{2}\left ( \frac{1}{\sqrt{1 + 100.5^2}} \cos (2.01 \omega_2 t - arctan(100.5)) - \frac{1}{\sqrt{1 + 0.5^2}} \cos (0.01 \omega_2 t - arctan(0.5))\right )\)
\(u(t) \approx \frac{e_m}{2} \cos(0.01 \omega_2 t)\)
Etude de circuits#
Circuits couplées
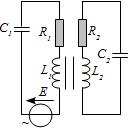
On considère le circuit ci-dessous. Les deux bobines sont sous influence mutuelle, c’est-à-dire qu’à la tension habituelle d’une bobine s’ajoute pour la bobine du circuit \(\alpha (\alpha \in \{1,2\})\), une tension \(M \frac{\rm{d}i_{\beta}}{\rm{dt}}\) avec \(\beta \in \{2,1\}\)
On supposera de plus que les composants sont égaux deux à deux. Déterminer en régime sinusoïdal forcé les représentations complexes des courants circulant dans chaque circuit puis les charges aux armatures des condensateurs.
Point utile pour cet exercice
\(\Longrightarrow\) Etude d’un circuit en RSF
\(\Longrightarrow\) Manipulation des complexes
Eléments de réponse (sans justification)
\(\underline{i_1} = \frac{\left (\frac{1}{jC \omega} + R + jL\omega \right) E}{{\left (\frac{1}{jC \omega} + R + jL\omega \right)}^2 - {(jM\omega)}^2}\)
\(\underline{i_1} = \frac{jM\omega E}{{\left (\frac{1}{jC \omega} + R + jL\omega \right)}^2 - {(jM\omega)}^2}\)
Les charges s’obtiennent en divisant par \(j \omega\): s’entrainer à simplifier ces diverses expressions.
Adaptation d’impédance
On considère le circuit ci-dessous. On veut que le dipôle composé des composants L, C variables et \(R_u\) fixée soit équivalent à une résistance pure \(R_g\) fixée.
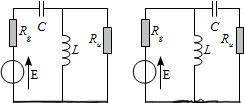
Déterminer suivant les valeurs relatives de \(R_u\) et \(R_g\) le circuit permettant cette réalisation et les valeurs de L et C à choisir.
Déterminer dans les conditions précédentes la puissance instantanée puis la puissance moyenne reçue par le dipôle équivalent.
Point utile pour cet exercice
\(\Longrightarrow\) Etude d’un circuit en RSF
\(\Longrightarrow\) Manipulation des complexes
\(\Longrightarrow\) Impédances usuelles
Eléments de réponse (sans justification)
Circuit 1 si \(R_u > R_g\). Il faut que \(L = \frac{R_u}{\omega}\sqrt{\frac{R_g}{R_u - R_g}}\) et \(C = \frac{1}{\omega R_g}\sqrt{\frac{R_g}{R_u - R_g}}\)
Circuit 2 si \(R_u < R_g\). Il faut que \(L = \frac{R_g}{\omega}\sqrt{\frac{R_u}{R_g - R_u}}\) et \(C = \frac{1}{\omega R_u}\sqrt{\frac{R_u}{R_g - R_u}}\)
Dans les deux cas, la puissance moyenne reçue est \(\frac{E^2}{8 R_g}\)
Système actif.#
Exercice
On considère le circuit ci-dessous. L’amplificateur linéaire intégré est supposé idéal fonctionnant en régime linéaire. Dans ces conditions, les courants entrant aux bornes + et - de l’amplificateur linéaire intégré sont nuls et la différence de potentiel \(\epsilon = V_+ - V_- = 0\).
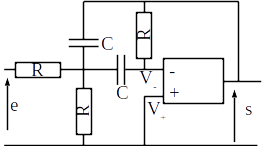
Déterminer par une étude rapide les comportements haute et basse fréquence du système pour la tension s.
Déterminer la tension s en régime sinusoïdal forcé et faire son étude fréquentielle (amplitude réelle et déphasage avec l’entrée). On pensera à vérifier la cohérence avec l’étude rapide précédente et à mettre la représentation complexe de s sous forme canonique.
Point utile pour cet exercice
\(\Longrightarrow\) Etude d’un circuit en RSF
\(\Longrightarrow\) Manipulation des complexes
\(\Longrightarrow\) Amplificateur linéaire intégré
Eléments de réponse (sans justification)
s et nulle à haute et basse fréquence.
\(\underline{s} = \frac{-\frac{\underline{e}}{2}}{1 j Q (x - \frac{1}{x})}\) avec \(x = \frac{\omega}{\omega_0}\), \(\omega_0 = \frac{\sqrt{2}}{RC}\) et \(Q = \frac{1}{\sqrt{2}}\). Il faut ensuite passer en réel pour répondre à la question.
