Intérêt de l’étude fréquentielle (en ligne)¶
Cette partie ne présente pas d’élements à apprendre mais sert à comprenre l’intérêt du régime sinusoïdal forcé. Il est donc important de bien comprendre les raisonnements.
Rappel: Linéarité¶
Principe de linéarité
On rappelle qu’un système linéaire est un système dont les équations différentielles décrivant l’évolution des grandeurs sont linéaires. Pour ce faire, il doit être composé uniquement de dipôle linéaires.
Soit une fonction \(f(t) = f_1(t) + f_2(t)\) et une équation différentielle homogène en y(t) \(f(y^{(k)},...,y',y)=0\). Si on peut trouver deux solutions particulières \(y_1(t)\) et \(y_2(t)\) respectivement pour les équations différentielles \(f(y^{(k)},...,y',y)=f_1(t)\) et \(f(y^{(k)},...,y',y)=f_2(t)\), alors la fonction \(y(t) = y_1(t) + y_2(t)\) est solution particulière de l’équation différentielle \(f(y^{(k)},...,y',y)=f(t)\).
Intérêt en physique
L’intérêt en physique est qu’on va pouvoir étudier la réponse forcée d’un système linéaire (on rappelle qu’il s’agit d’une solution particulière de l’équation avec second membre) à des entrées simples puis déduire son comportement pour des réponses plus complexes. Et comme on va le voir, on va pouvoir ramener l’étude d’un système physique linéaire à l’étude de sa réponse à une entrée sinusoïdale, on parlera d’étude fréquentielle.
Rappel: Décomposition spectrale¶
Etude fréquentielle.
On rappelle que l’on peut décomposer un signal \(s(t)\) comme une somme de signaux sinusoïdaux de fréquences différentes. Si l’on a principalement traité le cas de décomposition discrète, on peut rappeler que l’on peut décomposer un signal comme une somme continue de fréquence.
Si l’on étudie la réponse forcée d’un signal sinusoïdal de fréquence quelconque f et d’amplitude quelconque u pour un système linéaire, on peut déterminer la réponse forcée du système à tout signal.
En effet, la réponse forcée à un signal sinusoïdal de fréquence quelconque donne la réponse forcée à tout sinusoïde (logique !).
Et comme tout signal se décompose comme une somme de sinusoïdes, il vient que la réponse forcée d’un système linéaire à un tel signal sera la somme (principe de linéarité) des réponses forcées à chaque sinusoïdes (décomposition spectrale) obtenues grâce à l’étude de la réponse d’un sinusoïde quelconque.
Il vient qu’il suffit d’étudier la réponse forcée d’un système linéaire à une entrée sinusoïdale. On parlera d’étude fréquentielle.
Exemple
On va montrer le principe sur un exemple: l’étude d’une réponse d’un circuit RC. On synthétisera le principe d’étude par la suite. Il n’est pas conseillé de réfléchir à l’exercice au préalable. Passez directement à la correction.
On considère le circuit ci-dessous où la tension E est sous la forme \(e(t) = u_{1m} \cos \omega_1 t + u_{2m} \cos \left(\omega_2 t + \frac{\pi}{3}\right)\).
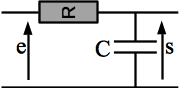
Déterminons le régime forcé du dipôle RC dans le circuit précédent. On déterminera la tension \(s(t)\) aux bornes du condensateur.
Méthode de résolution
On présente ici la méthode générale qui nécessite la détermination d’une solution particulière avec un second membre sinusoïdale. On se contentera ici de donner directement la réponse à cette question pour préciser les méthodes par la suite.
Méthode générale
L’étude d’un tel circuit est basé sur plusieurs étapes (attention, on ne réalisera quelque fois que certaines étapes suivants les besoins):
Étudier la réponse du circuit en régime forcé pour une grandeur sinusoïdale quelconque. C’est l’étude fréquentielle à proprement parler.
Décomposer le signal d’entrée étudié en une somme de sinusoïdes (ici, c’est déjà fait - on rappelle la nécessité de linéariser lorsqu’on est en présence d’un produit de sinusoïdes).
Déterminer la réponse forcée à chaque composante sinusoïdale du signal puis en déduire la réponse forcée pour le signal d’entrée complet en utilisant la linéarité du système.
1. Etude fréquentielle
On considère une entrée sinusoïdale \(e(t) = e_m \cos \left (\omega t \right)\). On cherche le régime forcé vers lequel tend le circuit. On observe expérimentalement qu’il s’agit d’un régime sinusoïdal forcé, c’est-à-dire que toutes les grandeurs du circuit vont osciller de manière sinusoïdale à la même pulsation que l’entrée, soit une pulsation \(\omega\).
Une étude de ce régime forcé (elle sera expliquée par la suite, c’est le coeur du chapitre) montre que le régime forcé est alors:
Note
On observe ici les deux grandeurs importantes qu’on cherchera à déterminer lors d’une étude fréquentielle - on rappelle étude de la réponse forcée à un sinusoïde: l’amplitude de la sortie et le déphasage entrée-sortie. Ces deux grandeurs dépendent de la fréquence et l’étude fréquentielle consiste en général à étude cette dépendance.
2.3. Décomposition et réponse complète
Ici, la décomposition spectrale est déjà faite. On va étudier la réponse à chaque composant.
Première composante \(u_{1m} \cos \omega_1 t\).
Ici, l’amplitude de l’entrée est \(u_{1m}\), la pulsation \(\omega_1\) et la phase \(\omega_1 t\). Il vient que l’amplitude de sortie sera \(\frac{u_{1m}}{\sqrt{1 + {(RC \omega_1)}^2}}\)
Le déphasage \(- \arctan RC \omega _1\).
Soit un signal en sortie: \(s_1(t) = \frac{u_{1m}}{\sqrt{1 + {(RC \omega_1)}^2}} \cos \left ( \omega_1 t - \arctan RC \omega _1\right)\)
Deuxième composante \(u_{2m} \cos \omega_2 t + \frac{\pi}{3}\).
Ici, l’amplitude de l’entrée est \(u_{2m}\), la pulsation \(\omega_2\) et la phase \(\omega_2 t + \frac{\pi}{3}\). Il vient que l’amplitude de sortie sera \(\frac{u_{2m}}{\sqrt{1 + {(RC \omega_2)}^2}}\)
Le déphasage \(- \arctan RC \omega _2\).
Soit un signal en sortie: \(s_2(t) = \frac{u_{2m}}{\sqrt{1 + {(RC \omega_2)}^2}} \cos \left ( \omega_2 t + \frac{\pi}{3} - \arctan RC \omega _2\right)\)
La réponse au signal \(e(t)\) sera donc:
Bilan
On présente ici la méthode générale d’étude donnée précédemment. Il reste une partie qui a été donnée sans explication: l’étude fréquentielle à proprement parler. Il s’agit:
d’observer qu’un régime sinusoïdal forcé est un régime où les grandeurs oscillent à la même pulsation que l’entrée. (Cette observation sera affirmée en cours puis observée en TP).
d’apprendre à chercher la réponse forcée et plus précisément ses caractéristiques: amplitude et phase (ou déphasage avec l’entée). Nous verrons que la méthode utilisée change des études précédents: on introduira les grandeurs complexes.
d’étudier ses caractéristiques pour connaître le comportement fréquentiel (c’est-à-dire par rapport à la fréquence) du système (aux hautes fréquences, aux basses fréquences… ) de manière à prévoir, même qualitativement son comportement face à un signal plus complexe (amplification, filtrage… )
Linéarité et spectre¶
Important
Linéarité et spectre Un système linéaire ne peut ajouter de composante spectrale à un signal, c’est-à-dire que les composantes spectrales d’un signal en sortie d’un système linéaire sont forcément celle du signal d’entrée.