.ipynb .md .pdf

Binder

Contents

Caractéristiques d’un système d’ordre 2

On rappelle que dans un système d’ordre 2, les dérivées sont au maximum des dérivées secondes des grandeurs. Nous allons voir que le régime transitoire possède trois régimes possibles suivant les valeurs des composantes du circuit. On pourra se ramener pour déterminer le type de régime (apériodique, pseudo-périodique ou critique) à étudier la valeur d’un paramètre : le facteur de qualité (ou de manière équivalente le coefficient d’amortissement).

L’étude de la réponse temporelle permettra de montrer qu’il peut y avoir des dépassement et que cette fois la rapidité du système dépend du type de régime. Nous verrons notamment dans une activité que les régimes les plus rapides sont les régimes proches du régime critique.

Nous apprendrons aussi à étudier plus particulièrement les caractéristiques de chaque régime, notamment du régime pseudo-périodique (au moyen du décrément logarithmique pour ce dernier) et nous verrons comment distinguer ce régime des autres de manière graphique.

Un bilan énergétique sera aussi proposé.

Nous allons présenter des généralités sur les systèmes d’ordre 2 et nous les mettrons en avant sur un exemple coulissant basé sur le circuit suivant (appelé circuit RLC série en régime libre) :

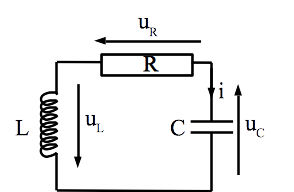
Cette fois, on suppose les conditions initiales connues à t=0 :

(70)$$\begin{array}{rl}i(t=0)& =i_0\\ u_C(t=0)& =0\end{array}$$

Système d’ordre 2: Différents régimes de fonctionnement

Système d’ordre 2: Forme canonique

Important

Fondamental : Forme canonique des systèmes d’ordre 2

L’équation différentielle qui régit l’évolution d’un système d’ordre 2 peut se mettre une des formes suivantes:

(71)$$\begin{array}{r}\frac{{\mathrm{d}}^2\mathrm{X}}{\mathrm{d}{\mathrm{t}}^2}(t)+\frac{{\omega }_0}{Q}\frac{\mathrm{d}\mathrm{X}}{\mathrm{d}\mathrm{t}}(t)+{\omega }_0^{2}X(t)=F(t)\\ \frac{{\mathrm{d}}^2\mathrm{X}}{\mathrm{d}{\mathrm{t}}^2}(t)+2\xi {\omega }_0\frac{\mathrm{d}\mathrm{X}}{\mathrm{d}\mathrm{t}}(t)+{\omega }_0^{2}X(t)=F(t)\end{array}$$

On appelle

• $Q$: le facteur de qualité du système

• $\xi$: le coefficient d’amortissement du système

• ${\omega }_0$: la pulsation propre du système

Exercice Cas du circuit RLC série: La tension uC

On peut appliquer une loi des mailles: $u_L+u_R+u_C=0$ soit $L\frac{\mathrm{d}\mathrm{i}}{\mathrm{d}\mathrm{t}}+Ri+u_C=0$. Il reste à utiliser $i=C\frac{\mathrm{d}{\mathrm{u}}_{\mathrm{C}}}{\mathrm{d}\mathrm{t}}$, il vient en organisant):

(72)$$\frac{{\mathrm{d}}^2{\mathrm{u}}_{\mathrm{C}}}{\mathrm{d}{\mathrm{t}}^2}+\frac{R}{L}\frac{\mathrm{d}{\mathrm{u}}_{\mathrm{C}}}{\mathrm{d}\mathrm{t}}+\frac{1}{LC}{u}_C=0$$

Il reste à identifier les facteurs:

$$\begin{array}{rlrlrl}{\omega }_0^2& =\frac{1}{LC}& ⟹& & {\omega }_0& =\frac{1}{\sqrt{LC}}\\ \frac{{\omega }_0}{Q}& =\frac{R}{L}& ⟹& & Q& =\frac{1}{R}\sqrt{\frac{L}{C}}\end{array}$$

Anciennes équations

Il est conseillé d’essayer de mettre sous forme canonique l’équation trouvée dans le chapitre précédent à titre d’entraînement.

Il est aussi conseillé de vérifier l’homogénéité des résultats et leur cohérence physique, même quand cela n’est pas fait dans le cours.

Système d’ordre 2: type de régime

Important

Fondamental : Type de régimes

La forme mathématique correspondant à la solution dépend de la valeur du facteur de qualité Q (ou du coefficient d’amortissement $\xi$) car ce dernier influe sur la valeur du discriminant de l’équation caractéristique $\mathrm{\Delta }$. A chaque expression différente correspond un type de régime:

	$\mathrm{\Delta }$	Q	$\xi$	Forme ESSM
Régime apériodique	> 0	< 1/2	> 1	$A\exp r_{1}t+B\exp r_{2}t$
Régime critique	= 0	= 1/2	= 1	$\exp r_{0}t(At+B)$
Régime pseudo-périodique	< 0	> 1/2	< 1	$\exp \lambda t(A\cos (\mathrm{\Omega }t)+B\sin (\mathrm{\Omega }t))$

On rappelle que :

• $r_1$ et $r_2$ sont les solutions de l’équation caractéristiques

• $r_0$ est la solution double lorsque le discriminant est nul

• $\lambda$ et $\mathrm{\Omega }$ sont respectivement la partie réelle de $r_1$ et $r_2$ et la partie imaginaire (en valeur absolue) de $r_1$ et $r_2$ lorsque le discriminant est négatif. On appelle $\mathrm{\Omega }$ la pseudo-pulsation du système.

Relation entre les paramètres

Il est conseillé de s’entraîner à exprimer les paramètres précédents en fonction de ${\omega }_0$ et Q (ou ${\omega }_0$ et $\xi$).

Système d’ordre 2 : Régime apériodique

Régime apériodique: Solution analytique

Solution de l’équation homogène
On rappelle que la solution de l’équation homogène dans le cas où $\mathrm{\Delta }>0$, c’est-à-dire $Q<1/2$ (ou $\xi >1$ est:

(73)$$X(t)=A{\exp }^{r_{1}t}+B{\exp }^{r_{2}t}$$

avec:

$$\begin{array}{r}{r}_1=-\frac{{\omega }_0}{2Q}+\sqrt{\frac{{\omega }_0^2}{4Q^2}-{\omega }_0^2}\\ r_2=-\frac{{\omega }_0}{2Q}-\sqrt{\frac{{\omega }_0^2}{4Q^2}-{\omega }_0^2}\end{array}$$

Analyse des expressions
Remarquons que dans le cas où les coefficients sont positifs, les deux racines sont négatives: on retrouve le principe de stabilité du système.

Ces racines (la moins grande) seront aussi associées au temps caractéristiques qui dépend donc de ${\omega }_0$ et de Q.

On pourrait montrer (HP) qu’une telle expression ne peut avoir qu’un seul extremum local (ou 0).

Exemple de tracés temporels et portrait de phase

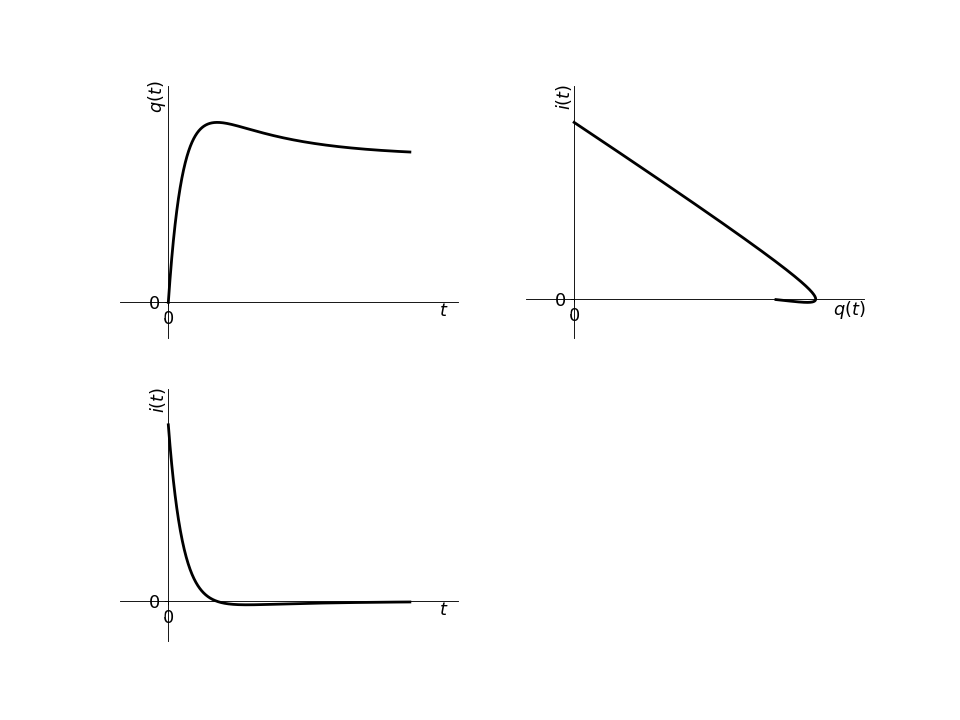
Exemple : Cas du RLC série: Détermination complète

On se propose de rechercher les constantes d’intégration dans le cas particuliers du RLC série en régime libre. (Il est conseillé de s’entraîner à le faire seul avant de regarder la réponse).

On a les expressions:

$$\begin{array}{rl}{u}_C(t)& =A{\exp }^{r_{1}t}+B{\exp }^{r_{2}t}\\ i(t)=C\frac{\mathrm{d}{\mathrm{u}}_{\mathrm{C}}}{\mathrm{d}\mathrm{t}}& =CA{r}_1{\exp }^{r_{1}t}+CB{r}_2{\exp }^{r_{2}t}\end{array}$$

soit les conditions initiales:

$$\begin{array}{rl}{u}_C(t=0)& =A+B=0⟹A=-B\\ i(t=0)& =C(r_1-r_2)A=i_0⟹A=\frac{i_0}{C(r_1-r_2)}\end{array}$$

Il vient les expressions:

$$\begin{array}{rl}{u}_C(t)& =\frac{i_0}{C(r_1-r_2)}({\exp }^{r_{1}t}-{\exp }^{r_{2}t})\\ i(t)=C\frac{\mathrm{d}{\mathrm{u}}_{\mathrm{C}}}{\mathrm{d}\mathrm{t}}& =\frac{C{i}_0}{C(r_1-r_2)}(r_1{\exp }^{r_{1}t}-r_2{\exp }^{r_{2}t})\end{array}$$

Régime critique

Régime critique: Solution analytique

Solution de l’équation homogène
On rappelle que la solution de l’équation homogène dans le cas où $\mathrm{\Delta }=0$, c’est-à-dire $Q=1/2$ (ou $\xi =1$ est:

(74)$$X(t)={\exp }^{r_{0}t}(At+B)$$

avec:

(75)$$r_0=-\frac{{\omega }_0}{2Q}=-{\omega }_0$$

Analyse des expressions
Remarquons que dans le cas où les coefficients sont positifs, la racine double est négative: on retrouve le principe de stabilité du système.

Cette racine sera aussi associée au temps caractéristiques qui dépend donc de ${\omega }_0$ et de Q.

On pourrait montrer (HP) qu’une telle expression ne peut avoir qu’un seul extremum local (ou 0).

Exemple de tracés temporels et portrait de phase

Remarquons qu’il y a beaucoup de similarités avec le régime apériodique en terme de tracé. Pris séparément, on ne peut pas savoir si un tel tracé vient d’un régime apériodique ou critique.

Nous verrons en activité un moyen de comparer les deux tracés (quand on a les deux).

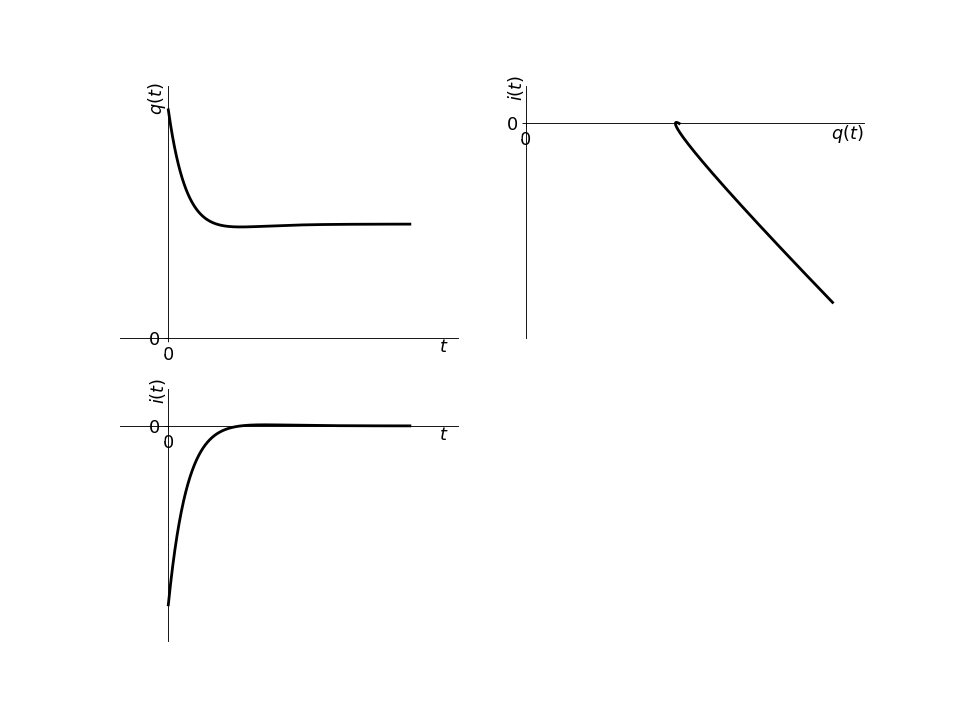
Exercice Cas du RLC série : Détermination complète

On se propose de rechercher les constantes d’intégration dans le cas particuliers du RLC série en régime libre. (Il est conseillé de s’entraîner à le faire seul avant de regarder la réponse).

On a les expressions:

$$\begin{array}{rl}{u}_C(t)& ={\exp }^{r_{0}t}(At+B)\\ i(t)=C\frac{\mathrm{d}{\mathrm{u}}_{\mathrm{C}}}{\mathrm{d}\mathrm{t}}& =C{\exp }^{r_{0}t}(r_{0}At+r_{0}B+A)\end{array}$$

soit les conditions initiales:

$$\begin{array}{rl}{u}_C(t=0)& =B=0\\ i(t=0)& =CA=i_0⟹A=\frac{i_0}{C}\end{array}$$

Il vient les expressions:

$$\begin{array}{rl}{u}_C(t)& =\frac{i_0}{C}{\exp }^{{\omega }_{0}t}t\\ i(t)=C\frac{\mathrm{d}{\mathrm{u}}_{\mathrm{C}}}{\mathrm{d}\mathrm{t}}& =i_0{\exp }^{{\omega }_{0}t}({\omega }_{0}t+1)\end{array}$$

Régime pseudo-périodique

Régime pseudo-périodique: Solution analytique

Solution de l’équation homogène
On rappelle que la solution de l’équation homogène dans le cas où $\mathrm{\Delta }<0$, c’est-à-dire $Q>1/2$ (ou $\xi <1$ est:

$$\begin{array}{rl}X(t)& ={\exp }^{-\lambda t}(A\sin \mathrm{\Omega }t+B\cos \mathrm{\Omega }t)\\ & ={\exp }^{-\lambda t}(C\sin (\mathrm{\Omega }t+\varphi ))\end{array}$$

avec:

$$\begin{array}{rl}\lambda & =Re(r_{1,2})=-\frac{{\omega }_0}{2Q}\\ \mathrm{\Omega }& =|Im(r_{1,2})|={\omega }_0\sqrt{1-\frac{1}{4Q^2}}\end{array}$$

Analyse des expressions
Remarquons que dans le cas où les coefficients sont positifs, le coefficient de l’exponentielle (issue de la partie réelle des racines) est négatif: on retrouve le principe de stabilité du système.

Ce coefficient (la moins grande) sera aussi associé au temps caractéristiques qui dépend donc de ${\omega }_0$ et de Q.

Nous étudierons plus en détail la forme temporelle.

Cas du RLC série : Détermination complète

On se propose de rechercher les constantes d’intégration dans le cas particuliers du RLC série en régime libre. (Il est conseillé de s’entraîner à le faire seul avant de regarder la réponse).

On a les expressions:

$$\begin{array}{rl}{u}_C(t)& ={\exp }^{-\lambda t}(A{\sin }^{\mathrm{\Omega }t}+B{\cos }^{\mathrm{\Omega }t})\\ i(t)=C\frac{\mathrm{d}{\mathrm{u}}_{\mathrm{C}}}{\mathrm{d}\mathrm{t}}& =C{\exp }^{-\lambda t}((-\lambda A-\mathrm{\Omega }B){\sin }^{\mathrm{\Omega }t}+(-\lambda B+\mathrm{\Omega }A){\cos }^{\mathrm{\Omega }t})\end{array}$$

soit les conditions initiales:

$$\begin{array}{rl}{u}_C(t=0)& =B=0\\ i(t=0)& =C\mathrm{\Omega }A=i_0⟹A=\frac{i_0}{C\mathrm{\Omega }}\end{array}$$

Il vient les expressions:

$$\begin{array}{rl}{u}_C(t)& ={\exp }^{-\lambda t}\left(\frac{i_0}{C\mathrm{\Omega }}{\sin }^{\mathrm{\Omega }t}\right)\\ i(t)& ={\exp }^{-\lambda t}(-\lambda \frac{i_0}{\mathrm{\Omega }}{\sin }^{\mathrm{\Omega }t}+i_0{\cos }^{\mathrm{\Omega }t})\end{array}$$

Vérification de résultats

Homogénéité : On pourra observer que $\lambda$ et $\mathrm{\Omega }$ sont de même unité ($s^{-1}$) et que $C\mathrm{\Omega }$ est bien homogène à R (utiliser le fait que RC est homogène à un temps).

Régime pseudo-périodique: Tracé temporelle

Tracé temporelle
L’expression $X(t)={\exp }^{-\lambda t}\left(D{\sin }^{\mathrm{\Omega }t+\varphi }\right)$ permet de dessiner facilement l’évolution de X(t) en régime pseudo-périodique.

En effet, on remarque qu’il s’agit d’un signal sinsoïdal de pulsation $\mathrm{\Omega }$ ou plutôt pseudo-sinusoïdal car l’amplitude décroît de manière exponentielle.

Pour représenter X(t), il faut d’abord représenter son enveloppe exponentielle: $D{\exp }^{-\frac{{\omega }_{0}t}{2Q}}$. On représente alors à l’intérieur de l’enveloppe un sinusoïde (dont l’amplitude décroît) de pseudo-période $T=\frac{2\pi }{\mathrm{\Omega }}$.

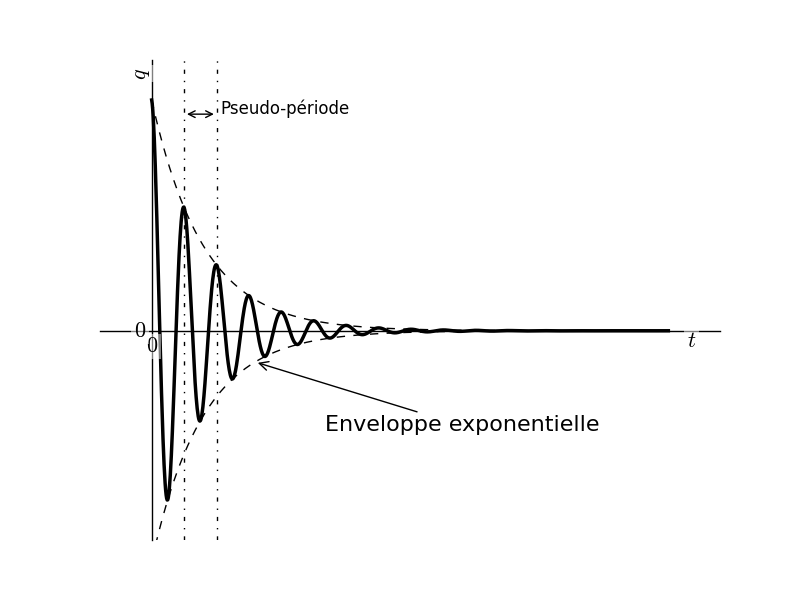
Attention

Pseudo-période et période propre

Il ne faut pas confondre la pseudo-période qu’on peut obtenir d’un tracé temporel et qui est reliée à la pseudo-pulsation et la période propre, reliée à la pulsation propre et qui n’apparaît pas directement dans les tracés temporel.

La période propre, comme la pulsation propre est un élément caractéristique issu de la forme canonique de l’équation : $T_0=\frac{2\pi }{{\omega }_0}$.

A l’inverse, la pseudo-période n’intervient pas dans la mise sous forme canonique mais apparaît dans les mesures expérimentales qu’on peut être amené à faire sur un système en régime pseudo-périodique.

Pour relier les deux, il faut le facteur de qualité.

Temps caractéristisque
L’analyse précédente permet de déterminer assez simplement le temps caractéristique du système. En effet, c’est l’exponentielle décroissante qui gouverne l’évolution du signal. Donc le temps caractéristique est: ${\tau }_c=\frac{2Q}{{\omega }_0}$

Régime pseudo-périodique: Décrément logarithmique

Amortissement et décroissance exponentielle
Dans le cas d’un régime pseudo-périodique, l’amplitude du pseudo-sinusoïde décroît de manière exponentielle. C’est la vitesse de décroissance qui va déterminer dans ce régime la force de l’amortissement.

Comme cette décroissance est exponentielle, nous allons utiliser un indicateur particulier pour quantifier l’amortissement.

Important

Définition : Décrément logarithmique.

Pour un régime pseudo-périodique de pseudo-période T, on définit le décrément logarithmique $\delta$ par:

(76)$$\delta =\ln \left(\frac{u(t)-u(t=+\mathrm{\infty })}{u(t+T)-u(t=+\mathrm{\infty })}\right)$$

Interprétation
On calcule l’écart à la valeur finale à deux instants t et t+T (ce second écart est plus faible pour un système stable). En faisant le rapport, on obtient un nombre d’autant plus grand que l’amortissement est fort. Le décrément est donc une mesure l’amortissement en régime pseudo-périodique.

Le fait que la décroissance soit exponentielle explique que l’on prenne le logarithmique du rapport. Nous allons voir que cela simplifie l’expression.

Important

Fondamental : Relation entre le décrément logarithmique et le facteur de qualité

On peut montrer que:

(77)$$\delta =\frac{2\pi }{\sqrt{4Q^2-1}}$$

Démonstration

$$\begin{array}{rl}\delta & =\ln \left(\frac{u(t)-u(t=+\mathrm{\infty })}{u(t+T)-u(t=+\mathrm{\infty })}\right)\\ & =\ln \left(\frac{e^{-\lambda t}(C\cos \mathrm{\Omega }t+\phi )}{e^{-\lambda (t+T)}(C\cos \mathrm{\Omega }(t+T)+\phi )}\right)\\ & =\ln \left(\frac{e^{-\lambda t}(\cos \mathrm{\Omega }t+\phi )}{e^{-\lambda (t+T)}(\cos \mathrm{\Omega }t+\mathrm{\Omega }T+\phi )}\right)\\ & =\ln \left(\frac{e^{-\lambda t}(\cos \mathrm{\Omega }t+\phi )}{e^{-\lambda (t+T)}(\cos \mathrm{\Omega }t+2\pi +\phi )}\right)\end{array}$$

soit :

$$\begin{array}{rl}\delta & =\ln \left(\frac{e^{-\lambda t}(\cos \mathrm{\Omega }t+\phi )}{e^{-\lambda (t+T)}(\cos \mathrm{\Omega }t+\phi )}\right)\\ & =\ln \left(\frac{e^{-\lambda t}}{e^{-\lambda (t+T)}}\right)\\ & =\ln \left(e^{\lambda T}\right)\\ & =\lambda T\end{array}$$

soit :

$$\begin{array}{rl}\delta & =\frac{{\omega }_0}{2Q}\frac{2\pi }{{\omega }_0\sqrt{1-\frac{1}{4Q^2}}}\\ & =\frac{2\pi }{2Q\sqrt{1-\frac{1}{4Q^2}}}\\ & =\frac{2\pi }{\sqrt{4Q^2-1}}\end{array}$$

Remarque

Analyse
On peut analyser l’expression précédente en remarquant que plus Q augmente, plus $\delta$ diminue. Il vient que en régime pseudo-périodique, plus Q est grand, plus l’amortissement est faible. On retrouve d’ailleurs ce principe avec le temps caractéristique qu’on a calculer précédemment.

Attention

Portée de l’étude précédente

Tout ce qui est établi ici (définition du décrément logarithmique, son expression en fonction de Q, sens à donner à Q) n’est vrai que si le régime est un régime pseudo-périodique.. Sinon, on ne peut pas faire une telle analyse (on ne peut d’ailleurs pas définit de pseudo-période.

Régime pseudo-périodique: Portrait de phase

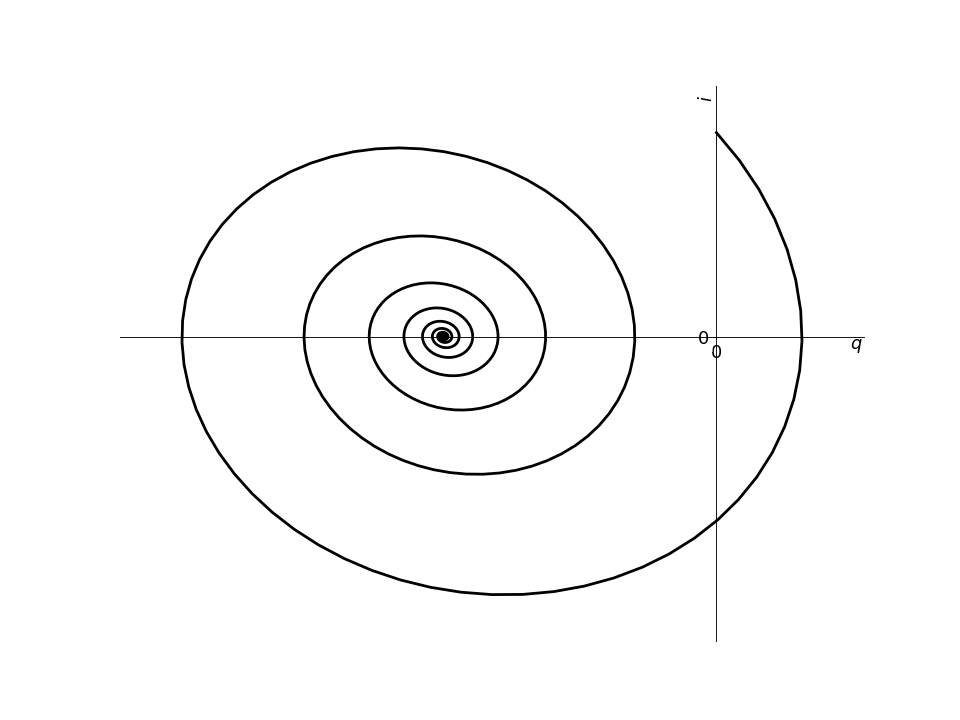
Allure du portrait de phase
Le portrait de phase en régime pseudo-périodique est une spirale elliptique convergeant vers le régime forcé.

Si l’on représente la dérivée $\dot{X}(t)$ en fonction de la fonction X(t), la spirale tourne dans le sens horaire.

Réponse indicielle d’un RLC série

On se propose de faire la synthèse des études précédentes sur l’exemple d’une réponse indicielle. On en profitera aussi pour voir la détermination des constantes avec l’autre forme de la solution en régime pseudo-périodique. Il est conseillé de s’entraîner à faire l’exercice avant de regarder les réponses.

Exercice

On considère le circuit suivant (E est constant). A t=0, le condensateur est complètement déchargé et aucun courant ne circule dans le circuit.

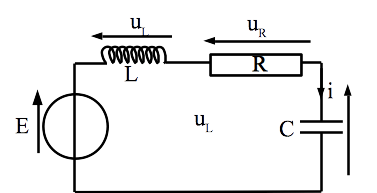
1. Exprimer la tension aux bornes du condensateur dans le nouveau régime forcé.

2. Déterminer l’équation différentielle qui régit l’évolution de la tension aux bornes du condensateur. En déduire les expressions du facteur de qualité et de la pulsation propre. Les comparer au cas du régime libre.

3. Déterminer l’expression de la tension aux bornes du condensateur pour t>0 dans le cas d’un régime pseudo-périodique.

4. Déterminer l’expression de la tension aux bornes du condensateur pour t>0 dans le cas d’un régime apériodique.

5. Déterminer l’expression de la tension aux bornes du condensateur pour t>0 dans le cas d’un régime critique.

Correction

Q1. Nouveau régime forcé
On peut considérer que le nouveau régime forcé est indépendant du temps (puisque E est constant). Le condensateur se comporte donc comme un interrupteur ouvert et l’intensité est donc nulle. Il vient que la tension aux bornes de la résistances est nulle.

La bobine elle se comporte comme un fil. La loi des mailles donne donc que $u_C(t=+\mathrm{\infty })=E$

Q2. Mise en équation
On peut écrire la loi des mailles $E=u_C+u_R+u_L=u_C+Ri+L\frac{\mathrm{d}\mathrm{i}}{\mathrm{d}\mathrm{t}}=0$. Soit avec $i=C\frac{\mathrm{d}{\mathrm{u}}_{\mathrm{C}}}{\mathrm{d}\mathrm{t}}$:

(78)$$\frac{{\mathrm{d}}^2{\mathrm{u}}_{\mathrm{C}}}{\mathrm{d}{\mathrm{t}}^2}+\frac{R}{L}\frac{\mathrm{d}{\mathrm{u}}_{\mathrm{C}}}{\mathrm{d}\mathrm{t}}+\frac{1}{LC}{u}_C=\frac{1}{LC}E$$

Il vient ${\omega }_0=\frac{1}{LC}$ et $Q=\frac{1}{R}\sqrt{\frac{L}{C}}$ soit les mêmes expressions que dans le cas du régime libre. C’est normal puisqu’il s’agit du même système (RLC série) confronté à une entrée différente (nulle dans un cas et égale à E dans l’autre).

Q3. Expression temporelle - Cas pseudo-périodique
La solution générale ESSM est alors:

(79)$$u_{c,0}(t)=D{\exp }^{-\frac{{\omega }_{0}t}{2Q}}(\cos \mathrm{\Omega }t+\phi )$$

avec $\mathrm{\Omega }={\omega }_0\sqrt{1-\frac{1}{4Q^2}}$ la pseudo-pulsation du système.

On recherche une solution particulière de l’équation avec second membre. On la cherche sous forme constante $u_C=U_0$. Les dérivées étant nulles, on trouve directement $U_0=E$. La solution complète est donc:

(80)$$u_c(t)=D{\exp }^{-\frac{{\omega }_{0}t}{2Q}}(\cos \mathrm{\Omega }t+\phi )+E$$

Il reste à utiliser les conditions initiales en utilisant le fait que $i=C\frac{\mathrm{d}{\mathrm{u}}_{\mathrm{C}}}{\mathrm{d}\mathrm{t}}$:

$$\begin{array}{rl}{u}_c(t=0)& =D\cos \phi +E=0\\ i(t=0)& =CD(-\mathrm{\Omega }\sin \phi -\frac{{\omega }_0}{2Q}\cos \phi )=0\\ ⟹\phi & =-\arctan \frac{{\omega }_0}{2Q\mathrm{\Omega }}=-\arctan \frac{1}{\sqrt{4Q^2-1}}\\ ⟹D& =-\frac{E}{\cos \phi }=-\frac{2Q}{\sqrt{4Q^2-1}}E\end{array}$$

Q4. Expression temporelle - Cas apériodique
La solution générale ESSM est alors:

(81)$$u_{c,0}(t)=A{\exp }^{r_{1}t}+B{\exp }^{r_{2}t}$$

avec $r_{1,2}=-\frac{{\omega }_0}{2Q}(1-\sqrt{1-4Q^2})$.

On recherche une solution particulière de l’équation avec second membre. On la cherche sous forme constante $u_C=U_0$. Les dérivées étant nulles, on trouve directement $U_0=E$. La solution complète est donc:

(82)$$u_c(t)=A{\exp }^{r_{1}t}+B{\exp }^{r_{2}t}+E$$

Il reste à utiliser les conditions initiales en utilisant le fait que $i=C\frac{\mathrm{d}{\mathrm{u}}_{\mathrm{C}}}{\mathrm{d}\mathrm{t}}$:

$$\begin{array}{r}{u}_c(t)=A+B+E=0\\ u_c(t)=A{r}_1+B{r}_2=0\\ ⟹A=-\frac{r_2}{r_2-r_1}E\\ ⟹B=-\frac{r_1}{r_1-r_2}E\end{array}$$

Q5. Expression temporelle - Cas critique
La solution générale ESSM est alors:

(83)$$u_{c,0}(t)={\exp }^{-\frac{{\omega }_{0}t}{2Q}}(At+B)$$

avec $r_{1,2}=-\frac{{\omega }_0}{2Q}(1-\sqrt{1-4Q^2})$.

On recherche une solution particulière de l’équation avec second membre. On la cherche sous forme constante $u_C=U_0$. Les dérivées étant nulles, on trouve directement $U_0=E$. La solution complète est donc:

(84)$$u_c(t)={\exp }^{-\frac{{\omega }_{0}t}{2Q}}(At+B)+E$$

Il reste à utiliser les conditions initiales en utilisant le fait que $i=C\frac{\mathrm{d}{\mathrm{u}}_{\mathrm{C}}}{\mathrm{d}\mathrm{t}}$:

$$\begin{array}{r}{u}_c(t)=B+E=0⟹B=-E\\ u_c(t)=-\frac{{\omega }_0}{2Q}B+A=0⟹A=-\frac{{\omega }_0}{2Q}E\end{array}$$

Vérification

On rappelle les vérification d’usage : Nouveau régime permanent et homogénéité. Il est conseillé de vérifier aussi l’homogénéité au niveau de l’équation différentielle, de Q (sans dimension) et de ${\omega }_0$.

Lorsqu’on détermine des conditions initiales, si le calcul est relativement complexe, il est aussi conseillé de vérifié qu’elles vérifient bien le système de départ.

previous

Caractéristiques d’un système d’ordre 1

next

Activités d’application