Système linéaire¶

Le but est de voir comment utiliser la méthode d’intégration d’Euler explicite pour étudier le régime transitoire d’un système d’équations. On a alors un système d’équations différentielles. On s’intéresse au pont de Wien en régime libre :

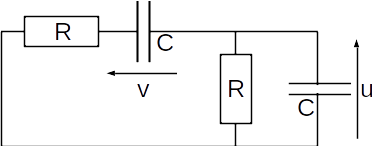
Circuit de Wien

Exercice :

Montrer par le calcul que ce circuit est régit par le système d’équation suivant :

\[\begin{split} {\rm{d} \over \rm{d}t} \begin{pmatrix} u\\ v \end{pmatrix} = \begin{pmatrix} - {1 \over RC} v - {2 \over RC} u\\ - {1 \over RC} v - {1 \over RC} u \end{pmatrix} \end{split}\]

On peut alors utiliser un schéma d’Euler explicite sur le vecteur :

\[\begin{split} Y(t)= \begin{pmatrix} u(t)\\ v(t) \end{pmatrix} \end{split}\]

dont la dérivée s’écrit :

(86)¶\[\begin{equation} {\rm{d}Y \over \rm{d}t} = F(Y, t) \end{equation}\]

avec :

\[\begin{split} F(Y, t) = \begin{pmatrix} - {1 \over RC} v - {2 \over RC} u\\ - {1 \over RC} v - {1 \over RC} u \end{pmatrix} \end{split}\]

_On rappelle que d’un point de vue vectoriel :

u = Y[0] et v = Y[1]_.
F prend comme argument un vecteur Y et renvoie un vecteur de taille 2.
On a techniquement pas besoin du temps puisque F ne dépend pas explicitement du temps mais on prendra l’habitutde de le mettre comme argument même si on ne l’utilise pas (pour des fonctions comme odeint).

Exercice :
Pour les études numériques, on prend \(R=1k\Omega\) et \(C= 1nF\).

Ecrire une fonction F(Y, t) qui prend comme argument le vecteur Y et l’instant t et qui renvoie un vecteur numpy de taille 2 correspondant au vecteur donné précédemment.

Ecrire une fonction euler(F, Y0, tf, pas) qui prend comme argument la fonction F, un vecteur Y0 donnant les conditions initiales \(u(0), v(0)\), et qui réalise l’intégration d’Euler par pas d’intégration de \(t=0\) à tf.Elle renverra un tableaux numpy à deux colonnes contenant pour chaque lignes les valeurs de Y aux temps \(t_k\) et un vecteur numpy contenant les temps \(t_k\).

Obtenir l’expression théorique de \(u(t)\) et \(v(t)\) par le calcul pour un jeu de conditions initiales \(u0, v0\) puis créer deux fonctions u_th(t, Y0) et v_th(t, Y0) qui renvoie un vecteur des valeurs de u (ou v) par l’expression théorique obtenue pour un vecteur de valeurs de temps t.

Obtenir puis tracer l’évolution temporelle de \(u(t)\) et \(v(t)\) par intégration numérique ainsi que par calcul théorique et comparer les deux tracés. On adaptera le pas d’intégration pour limiter les écarts. On prend \(u(0) = 0; v(0) = v_0 = 1V\).

Indications utiles :

Pensez à utiliser l’étude théorique pour choisir un temps tf adapté.

Electrocinétique

Système linéaire¶