Méthodes d’analyse d’un régime transitoire¶

Nous avons vu quelques caractéristiques du régime transitoire comme son temps caractéristique ou encore l’étude de régime forcé. L’étude du régime transitoire passe par l’étude de la réponse temporelle qu’il convient de déterminer. Pour cela il faut:

déterminer l’équation qui régit l’évolution de la grandeur qui nous intéresse. Nous verrons qu’il s’agit d’une équation différentielle et qu’elle possède certaines propriétés importantes
déterminer les conditions initiales qui permettront de déterminer les constantes d’intégration lors de la résolution. Il faut noter que souvent, ces dernières ne sont pas données mais doivent être déterminées.
Déterminer l’évolution temporelle (u(t) ou i(t) ou le deux) de la grandeur qui nous intéresse. Cela passe par la résolution de l’équation différentielle établie précédemment en utilisant les conditions initiales.

Mise en équation¶

Pour déterminer analytiquement l’évolution d’une grandeur, il faut pouvoir déterminer l’équation différentielle qui régit l’évolution de cette grandeur. Nous allons voir globalement les méthodes à disposition et les informations qu’on peut tirer de telles études.

Méthode: Déterminer l’équation différentielle (Lois de Kirchhoff)¶

On se propose ici de voir comment déterminer l’équation différentielle qui régit l’évolution d’une grandeur au moyen des lois de Kirchhoff.

Exercice

On considère le circuit suivant. L’interrupteur est ouvert depuis un temps long. A t=0, on ferme l’interrupteur.

Déterminer l’équation différentielle qui régit l’évolution de la tension aux bornes du condensateur.

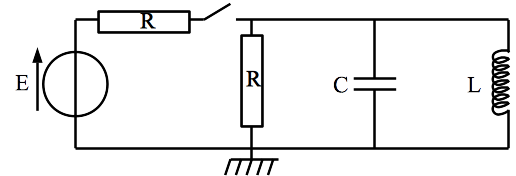
Correction

Paramétrage
Comme d’habitude, on commence par paramétrer le système. Les grandeurs introduites sont présentées sur le graphique.

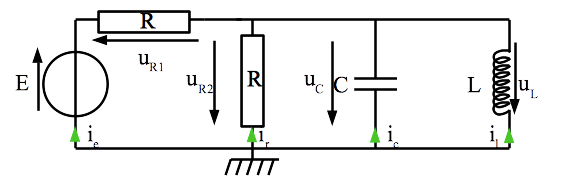
Rappelons aussi que les deux noeuds du haut peuvent être “rassemblés en un seul, ce qui évite d’avoir à considérer l’intensité qui circule dans la branche du haut au milieu.

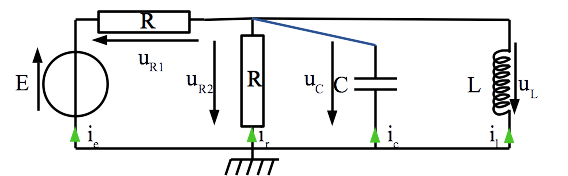
Mise en équation
On utilise les lois de Kirchhoff. Les deux points à bien faire attention sont:

Bien déterminer quelle sont les grandeurs qui entrent en jeu dans l’utilisation de relations tension-intensité pour C et L (ce n’est pas juste i ou u, c’est l’intensité qui circule dans le condensateur (resp. dans la bobine) et la tension aux bornes du condensateur (resp. de la bobine). On cherche ensuite leur expression sur le schéma pour écrire la bonne équation d’évolution.
Bien faire attention aux conventions. Le mieux, si on a le choix, est d’orienter C et L (comme R) en convention récepteur de manière à pouvoir utiliser les équations d’évolutions sont faire de faute de signe.
Ne pas forcément vouloir éliminer toutes les tensions ou toutes les intensités. Cette fois, on ne peut pas toujours exprimer une tension en fonction d’une intensité ou vice-versa à cause des dérivées.

Il convient par contre de bien penser à faire la différence entre ce qui nous intéresse de ce qu’on veut éliminer.

On rappelle que les grandeurs connues sont E, R, L et C et que la grandeur qu’on cherche est \(u_C\).

Toutes les intensités sont à éliminer, ainsi que les autres tensions.

Nous avons directement éliminer les tensions aux bornes des résistances et de la bobines car on sait qu’on ne les cherche pas ET qu’on peut les éliminer facilement à partir des équations d’évolutions.

A l’inverse, on élimine l’intensité qui circule dans le condensateur (et pas sa tension) car elle permet d’introduire directement la grandeur (\(u_C\)) qu’on recherche en éliminant une grandeur inintéressante (\(i_c\)).

Remarquons aussi qu’au niveau du choix des mailles, on a choisi trois mailles faisant directement intervenir \(u_C\) plutôt que des tensions (et indirectement des intensités) qu’on voudra faire disparaître.

(26)¶\[\begin{align} i_e + i_r + C \frac{\rm{d}u_C}{\rm{dt}} + i_l &= 0 \\ E - R i_e + u_C &= 0 \\ R i_r - u_C &= 0 \\ u_C - L \frac{\rm{d}i_l}{\rm{dt}} &= 0 \end{align}\]

On a 4 inconnues et 4 équations. Le système peut donc être résolu.

Manipulation du système
Une fois le système mis en place, il convient de réfléchir à une stratégie avant de se lancer (on rappelle que les grandeurs à éliminer sont les trois intensités). Remarquons que le choix des mailles a permis d’avoir un système simple car chacune des lois des mailles permet d’écrire une intensité (ou sa dérivée) en fonction de \(u_C\):

(27)¶\[\begin{align} i_e + i_r + C \frac{\rm{d}u_C}{\rm{dt}} + i_l &= 0 \\ i_e &= \frac{E + u_C}{R}\\ i_r &= \frac{u_C}{R} \\ \frac{\rm{d}i_l}{\rm{dt}} &= \frac{u_C}{L} \end{align}\]

Il suffit ensuire de remplacer dans la loi des noeuds (première équation) les différentes intensités.

(28)¶\[\begin{equation} \frac{E + u_C}{R} + \frac{u_C}{R} + C \frac{\rm{d}u_C}{\rm{dt}} + i_l = 0 \end{equation}\]

Dans le cas de \(i_l\), puisqu’on connaît sa dérivée, on va dériver la loi des noeuds pour faire apparaître \(\frac{\rm{d}i_l}{\rm{dt}}\).

Ne pas chercher à intégrer une grandeur (à cause des constantes d’intégration).

(29)¶\[\begin{equation} \frac{\frac{\rm{d}u_C}{\rm{dt}}}{R} + \frac{\frac{\rm{d}u_C}{\rm{dt}}}{R} + C \frac{\rm{d^2}u_C}{\rm{dt^2}} + \frac{u_C}{L} = 0 \end{equation}\]

Organisation de l’équation
Il convient d’organiser (en fonction des dérivées) l’équation correctement. Nous verrons plus tard qu’il existe même une forme “canonique” sous laquelle mettre l’équation pour faire apparaître des grandeurs particulières.

(30)¶\[\begin{equation} \frac{\rm{d^2}u_C}{\rm{dt^2}} + \frac{2}{RC} \frac{\rm{d}u_C}{\rm{dt}} + \frac{1}{LC} u_C = 0 \end{equation}\]

Analyse de l’équation

Homogénéité: Puisqu’une dérivée temporelle revient à diviser par un temps, on attend devant la dérivée première un facteur homogène à des \(s^{-1}\) (pour être homogène avec la dérivée seconde) et devant la fonction \(u_C\) un facteur homogène à des \(s^{-2}\).

On peut montrer que le produit RC est homogène à un temps (utiliser les équations d’évolutions de R et C). et que le produit LC est homogène à un temps au carré (idem). L’expression est bien homogène.

Sens physique: Le système est d’ordre 2. C’est ce qu’on attend d’un circuit possèdant un condensateur et une bobine.

Dans le système (sans la tension d’entrée), il n’y a que des dipôles passifs. On attend donc que le système soit stable.

Nous verrons par la suite qu’on peut déterminer si un système est stable où non. Vous pourrez alors reprendre l’équation obtenue et vérifier qu’elle correspond à un système stable.

Nouveau régime forcé: Une autre vérification possible qui peut même faire l’objet d’une étude à part entière est le régime forcé. On rappelle qu’on peut en effet déterminer le régime forcé à partir du schéma. On trouve \(u_{C,force} = 0\) (s’entraîner à le prouver).

On peut retrouver un régime forcé indépendant du temps en cherchant une solution constante à l’équation différentielle précédente.

Soit en cherchant \(u_C(t) = U_0\) l’équation \(0 + 0 + \frac{1}{LC} U_0 = 0\). On trouve bien la bonne expression: l’équation est cohérente.

Attention

Erreurs de calculs

Il y a de nombreuses erreurs de calculs possibles qu’on retrouve fréquemment dans ce genre d’étude. Citons notamment le fait de ne pas annuler la dérivée de E (qui est une constante).

De même à la fin, on a diviser par C. Il faut penser à diviser tous les termes de l’équation, y compris ceux de droite.

Méthode: Déterminer l’équation différentielle (utilisation des potentiels)¶

La loi des noeuds en terme de potentiels peut aussi être utilisée. Elle demande simplement quelques ajustements en fonction de ce qu’on utilise.

Exercice

On considère le circuit de l’exercice précédent. Déterminer l’équation différentielle qui régit l’évolution de l’intensité qui circule dans la bobine quand on fermé l’interrupteur.

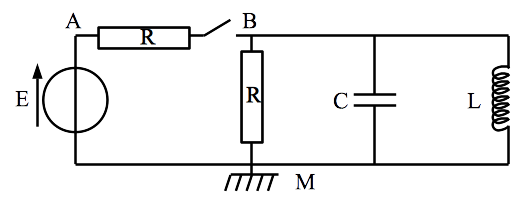
Correction

Paramétrage
Comme d’habitude, on paramètre les points de potentiels et on “choisit” une références des potentiels (elle est déjà imposée, ici M).

Au passage, on a \(V_A = E\)

Remarque: Aviez-vous bien remarqué qu’il n’y avait que 3 points de potentiels différents ?

Il n’y a qu’une seule inconnue \(V_B\). Ce n’est pas ce qu’on cherche (cette méthode aurait été beaucoup plus judicieuse pour chercher \(u_C\) mais nous voulons montrer que quelque soit la méthode, on peut aboutir). Il faudra établir ensuite une relation entre \(V_B\) et \(i_l\)

Mise en équation
On applique la loi des noeuds au point B. Il vient:

(31)¶\[\begin{equation} i_e + i_r + i_c + i_l = 0 \end{equation}\]

Pour la résistance et le condensateur, on peut directement utiliser la relation intensité-tension pour éliminer les intensités.

(32)¶\[\begin{equation} \begin{cases} i_e &= \frac{V_A - V_B}{R} = \frac{E - V_B}{R}\\ i_r &= \frac{V_M - V_B}{R} = - \frac{V_B}{R}\\ i_c &= C \frac{\rm{d}(V_M-V_B)}{\rm{dt}} = - C \frac{\rm{d}V_B}{\rm{dt}}\\ \end{cases} \Longrightarrow \frac{E - V_B}{R} - \frac{V_B}{R} - C \frac{\rm{d}V_B}{\rm{dt}} + i_l = 0 \end{equation}\]

Pour la bobine, c’est différent car on relie la dérivée de l’intensité à la différence de potentiel: \(V_M - V_B = L \frac{\rm{d}i_l}{\rm{dt}}\). Il va donc falloir dériver la loi des noeuds pour faire apparaître \(V_B\)

(33)¶\[\begin{equation} - \frac{2}{R} \frac{\rm{d}V_B}{\rm{dt}} - C \frac{\rm{d^2}V_B}{\rm{dt}^2} - \frac{1}{L} V_B = 0 \end{equation}\]

Remarquons qu’on obtient assez logiquement l’équation différentielle pour \(u_C\) obtenue précédemment (puisque \(u_C = V_B - 0\)). On voit que cette méthode pour déterminer \(u_C\) est de difficultés équivalente à la méthode présentée précédemment.

Du potentiel à l’intensité
Il est important de noter qu’on ne peut utiliser l’équation de la bobine car elle relie le potentiel à la dérivée de l’intensité. Il faudrait donc intégrer l’équation ce qui nécessiterait des constantes d’intégration (qu’on ne connaît pas nécessairement).

On va utiliser l’équation (obtenue des équations précédentes):

(34)¶\[\begin{equation} i_l = C \frac{\rm{d}V_B}{\rm{dt}} + \frac{2}{R} V_B - \frac{E}{R} \end{equation}\]

On va établir une expression pour chaque terme de la somme précédente et sommer l’ensemble. Ainsi (on a simplement réorganisé puis manipulé - multiplication et dérivation - l’équation en \(V_B\) obtenue précédemment):

(35)¶\[\begin{align} \frac{\rm{d^2} (\frac{2}{R} V_B)}{\rm{dt}^2} + \frac{2}{RC} \frac{\rm{d} (\frac{2}{R} V_B)}{\rm{dt}} + \frac{1}{LC} (\frac{2}{R} V_B) &= \frac{2}{R} \times 0 = 0\\ \frac{\rm{d^2} (C \frac{\rm{d}V_B}{\rm{dt}})}{\rm{dt}^2} + \frac{2}{RC} \frac{\rm{d} (C \frac{\rm{d}V_B}{\rm{dt}})}{\rm{dt}} + \frac{1}{LC} (C \frac{\rm{d}V_B}{\rm{dt}}) &= C \frac{\rm{d}0}{\rm{dt}} = 0\\ \end{align}\]

soit en sommant:

(36)¶\[\begin{equation} \frac{\rm{d^2} (C \frac{\rm{d}V_B}{\rm{dt}} + \frac{2}{R} V_B)}{\rm{dt}^2} + \frac{2}{RC} \frac{\rm{d} (C \frac{\rm{d}V_B}{\rm{dt}} + \frac{2}{R} V_B)}{\rm{dt}} + \frac{1}{LC} (C \frac{\rm{d}V_B}{\rm{dt}} + \frac{2}{R} V_B) = 0 + 0 \end{equation}\]

Il ne reste plus qu’à ajouter à gauche est à droite le terme \(\frac{-E}{RLC}\) et on obtient l’équation en \(i_l\) (on a rajouter aussi ce termes dans les dérivées temporelles sans modification puisqu’il s’agit d’un terme constant):

(37)¶\[\begin{align} &\frac{\rm{d^2} (C \frac{\rm{d}V_B}{\rm{dt}} + \frac{2}{R} V_B -\frac{E}{R})}{\rm{dt}^2} + \frac{2}{RC} \frac{\rm{d} (C \frac{\rm{d}V_B}{\rm{dt}} + \frac{2}{R} V_B -\frac{E}{R})}{\rm{dt}} + \frac{1}{LC} (C \frac{\rm{d}V_B}{\rm{dt}} + \frac{2}{R} V_B -\frac{E}{R})= -\frac{1}{LC} \frac{E}{R}\\ \Longrightarrow& \frac{\rm{d^2} i_l}{\rm{dt}^2} + \frac{2}{RC} \frac{\rm{d} i_l}{\rm{dt}} + \frac{1}{LC} i_l = -\frac{E}{RLC} \end{align}\]

Vérification de l’équation

Les vérifications sont similaires au cas précédent. On pensera à vérifier notamment le régime forcé.

Commentaire sur l’utilisation de la loi des noeuds.

Malgré ce que laisse à penser cet exemple volontairement complexe (cf. suite), la loi des noeuds en terme de potentiel permet souvent de simplifier les problème quand on cherche à déterminer une tension ou un potentiel (on peut s’en rendre avec la détermination de \(V_B\)). Quand on cherche à déterminer une intensité. Il faut réfléchir. Suivant les cas, une méthode sera préférable ou pas…

Remarques sur les équation différentielles obtenues¶

Equations obtenues
Rappelons les deux équations obtenues. On donne aussi les équation d’évolution des trois autres intensités (s’entraîner à les déterminer est un bon exercice).

(38)¶\[\begin{equation} \frac{\rm{d^2} i_l}{\rm{dt}^2} + \frac{2}{RC} \frac{\rm{d} i_l}{\rm{dt}} + \frac{1}{LC} i_l = -\frac{E}{RLC} \end{equation}\]

(39)¶\[\begin{equation} \frac{\rm{d^2}u_C}{\rm{dt^2}} + \frac{2}{RC} \frac{\rm{d}u_C}{\rm{dt}} + \frac{1}{LC} u_C = 0 \end{equation}\]

(40)¶\[\begin{equation} \frac{\rm{d^2}i_r}{\rm{dt^2}} + \frac{2}{RC} \frac{\rm{d}i_r}{\rm{dt}} + \frac{1}{LC} i_r = 0 \end{equation}\]

(41)¶\[\begin{equation} \frac{\rm{d^2}i_c}{\rm{dt^2}} + \frac{2}{RC} \frac{\rm{d}i_c}{\rm{dt}} + \frac{1}{LC} i_c = 0 \end{equation}\]

(42)¶\[\begin{equation} \frac{\rm{d^2}i_e}{\rm{dt^2}} + \frac{2}{RC} \frac{\rm{d}i_e}{\rm{dt}} + \frac{1}{LC} i_e = \frac{E}{RLC} \end{equation}\]

Explications
Il ne s’agit pas ici de démontrer cette propriété (qui ne peut être utilisée telle qu’elle de toute façon) mais d’en expliquer un peu les raisons et les implications.

La raison est qu’on peut toujours obtenir une grandeur en fonction d’une (des autres) par des relations linéaires. Et l’on commence à faire des combinaisons linéaires d’une grandeur avec ses dérivées, elle sera toujours solution de la même équation différentielle.

On a vu ce principe quand on cherché \(i_l\) à partir de l’équation en \(V_B\). Notons qu’en pratique on le fait rarement.

Régime forcé à partir de l’équation différentielle.
Comme nous l’avons précisé dans les exercices, on peut déterminer un régime forcé indépendant du temps à partir des équations.

On rappelle que cela n’a de sens que si le régime forcé EST indépendant du temps. Lorsqu’on a établi l’équation différentielle, on peut vérifier si c’est le cas en regardant si le second membre est constant. Si c’est le cas, le régime forcé le sera aussi et on peut le déterminer en cherchant une solution particulière de l’équation avec second membre sous la forme d’une constante.

Variation du second membre
Avec la méthode présentée ci-dessus, li est évident que le second membre doit varier puisque le comportement de chaque grandeur sera a priori différent en régime forcé.

Il faut donc bien noter cette différence entre l’équation homogène, qui caractérise le régime transitoire et le second membre qui va permettre de déterminer le régime forcé .

Attention à ne pas confondre: il est évident que l’équation homogène (donc les caractéristiques du système) influe AUSSI sur le régime forcé. Mais le second membre n’influe pas lui sur la rapidité du régime transitoire ou le type de régime (nous les détaillerons par la suite mais on peut déjà relier ces “types” de régime à la solution mathématique de l’équation homogène).

Ajoutons aussi que le second membre dépend de E et c’est logique puisque le régime forcé dépend de la grandeur d’entrée.

Les conditions initiales…
Si l’on relie les remarques précédentes à l’étude habituelle d’une équation différentielle, on remarque que:

la recherche de la solution générale ESSM - associée à l’équation homogène - ne dépend que des caractéristiques du système.
la recherche du régime forcé - associée à la solution particulière de l’équation avec second membre - dépend des caractéristiques du circuit, de la grandeur d’entrée et de la grandeur considérée dans le circuit.
Reste enfin les constantes d’intégration qui sont beaucoup plus “accidentelles”: elles vont dépendre de toutes les grandeurs citées précédemment mais aussi de l’état initial du système (et donc souvent de l’état dans lequel était le système AVANT de subir une perturbation).

Détermination des conditions initiales¶

Combien de condition initiales¶

Conditions initiales
On rappelle que pour pouvoir résoudre de manière unique une équation différentielle, il faut connaître la valeur de la fonction (voire de ses dérivées) en certains points.

Il faut donc déterminer (ou connaître) les valeurs des grandeurs qui nous intéressent à certains instants.

Très souvent, on les détermine au moment (initial) où la perturbation se produit, c’est pourquoi on parle de conditions initiales.

Nombre de conditions initiales
Le principe est simple. C’est l’ordre de l’équation qui va déterminer le nombre de conditions initiales nécessaires.

Dans l’exemple précédent, le système est d’ordre 2. Il faut donc 2 conditions initiales (si possible la valeur de la fonction et de sa dérivée, c’est le plus simple).

Continuité des grandeurs¶

Problème de continuité
Comme nous l’avons évoqué précédemment, le système est souvent soumis à une brusque variation de la grandeur d’entrée, souvent modélisée par un échelon.

Cela signifie que la grandeur d’entrée au temps \(t_0\) où se produit la perturbation est discontinue. Il vient que les autres grandeurs du système __sont a priori discontinues en \(t_0\).

C’est un gros problème car il nous faut déterminer les constantes d’intégration à partir de valeurs des signaux après la perturbation (conditions initiales). Et en général, on ne connaît bien le système qu’avant la perturbation (parce qu’il était “au repos” dans un état depuis un temps long\footnote{Temps long —La notion de temps long est important pour l’étude de régimes transitoires. Elle signifie qu’on a attendue assez longtemps pour que le régime transitoire soit terminée. On peut considérer alors qu’on est en régime forcé.

Remarque: Un temps “long” signifie qu’on a attendu un temps grand devant le temps caractéristique du système considéré.

Il faut noter que dans le cas de circuit électrique, le temps caractéristique est de l’ordre de quelques millisecondes voire beaucoup moins. Dans ces conditions, un dixième de seconde est… un temps long !

}).

Pour résoudre ce problème, on va utiliser des grandeurs dont on sait qu’elle sont par propriété continues.

Important

Fondamental : Grandeurs nécessairement continues

La tension aux bornes d’un condensateur est une grandeur nécessairement continue.
L’intensité qui circule dans une bobine est une grandeur nécessairement continue.

Démonstration
La dérivée de ces deux grandeurs intervient dans les relations intensité tension de la bobine et du condensateur. Elles sont donc dérivables et donc nécessairement continues.

Méthode: Déterminer des conditions initiales¶

Cet exercice explique comment déterminer les conditions initiales nécessaires à la résolution de l’équation différentielle.

Exercice

On considère le circuit. L’interrupteur est ouvert depuis un temps long. A t=0, on ferme l’interrupteur. On rappelle qu’on a déterminé l’équation différentielle pour \(u_C\) et \(i_l\) pour t > 0 (prendre les notations précédentes). Déterminer les conditions initiales nécessaires à la résolution de ces équations.

Correction

Quelles grandeurs déterminer dans l’ancien régime forcé
Le but n’est pas de caractériser entièrement l’ancien régime forcé mais de déterminer les grandeurs qui nous permettent d’avoir des informations sur les conditions initiales, c’est-à-dire sur __l’instant \(t=0^+\).

A cause de la discontinuité introduite par la fermeture brutale de l’interrupteur, les grandeurs peuvent être discontinue à t=0. On ne peut donc obtenir des information à \(t=0^+\) des informations qu’on a à \(t=0^-\) que des grandeurs continues par propriétés: la tension aux bornes du condensateur et l’intensité circulant dans la bobine..

Les grandeurs qu’il convient de calculer dans l’ancien régime forcé sont donc ces grandeurs.

Grandeurs avant fermeture de l’interrupteur
L’étude de l’ancien régime permanent donne \(u_C(t=0^-) = 0\) (la bobine assimilable à un fil impose une tension nulle aux bornes du condensateur) et \(i_l(t=0^-) = 0\) (loi des mailles).

Ces grandeurs étant continues, il vient \(\boxed{i_l(t=0^+)= 0}\) et \(\boxed{u_C(t=0^+) = 0}\)

Attention

Lien entre grandeurs étudiés et grandeurs continues

IL N’Y EN A AUCUN…

Le fait qu’on s’intéresse à \(u_C\) et \(i_l\) et que ce sont ces grandeurs qu’on calcule dans l’ancien régime permanent n’a aucun rapport.

On calcule ces grandeurs parce qu’elles sont continues.

Etude du circuit à t=0. Cas de la bobine.
On rappelle qu’il faut les valeurs de deux grandeurs puisque le circuit est d’ordre 2 (cf. les équations établies précédemment). Techniquement, on dispose déjà de deux grandeurs. On peut donc résoudre. Cela dit, il peut être plus simple d’étudier le circuit pour obtenir la valeur de \(i_l(t=0^+) = 0\) et de \(\frac{\rm{d}i_l}{\rm{dt}}(t=0^+)\) pour résoudre l’équation différentielle comme on a l’habitude de le faire (ce n’est pas obligatoire si on sait bien manipuler les expressions ensuite).

Ici, on connaît déjà la valeur de l’intensité (\(i_l(t=0^+) = 0\)) et \(\frac{\rm{d}i_l}{\rm{dt}}(t=0^+) = \frac{u_L}{L} = \frac{u_C}{L} = 0\)

On dispose donc des deux conditions initiales pour résoudre l’équation.

Etude du circuit à t=0. Cas du condensateur.
Cette fois, on connaît \(u_C(t=0^+) = 0\) mais pas sa dérivée. Il va falloir utiliser les lois de Kirchhoff.

On a \(\frac{\rm{d}u_C}{\rm{dt}}(t=0^+) = \frac{i_c(t=0^+)}{C}.\) Utilisons la loi des noeuds \(i_e + i_r + i_l + i_c = 0\)

On a déjà \(i_l = 0\). Remarquons que \(i_r = \frac{u_{R2}}{R} = \frac{u_{C}}{R} = 0\) donc \(i_c = - i_e\).

On peut de plus écrire une loi des mailles \(E - R i_e + R i_r = 0\) soit \(i_e = \frac{E}{R}\).

Il vient: \(\frac{\rm{d}u_C}{\rm{dt}}(t=0^+) = - \frac{E}{RC}\)

Attention

Etude à un instant

On ne peut pas utiliser les relations des bobines et condensateurs car ces relations font intervenir des dérivées. Or on étudie le circuit en un point, pas sur une durée. On n’a pas d’information sur la fonction \(u_C\), uniquement se son image en t=0.

Et ce qu’on a calculé est bien l’image de la dérivée de \(u_C\) à \(t=0^+\).

On remarquera que cette dérivée n’est pas continue.

Pour ne pas se tromper

Il est conseillé de préciser si l’on calcule une valeur d’une fonction à un instant donné ou bien si l’on la calcule pour tout instant t sur intervalle.

Une bonne manière de ne pas se tromper est de bien écrire \(u(t=0^+)\) ou \(u(t)\) suivant les besoins.

Etude de l’évolution temporelle¶

Rappel : Méthode de résolution
On rappelle ici la méthode de résolution d’une équation différentielle. Insistons sur le fait que l’ordre de résolution est fondamental.

Déterminer à partir de l’équation homogène la solution générale de l’équation sans second membre.
Déterminer une solution particulière de l’équation avec second membre. En physique, on cherchera une solution particulière correspondant au régime forcé.. Ainsi, si le second membre est constant, on cherchera une solution constante. Ne pas utiliser la méthode de la variation de la constante en physique.
En déduire la solution générale de l’équation avec second membre en sommant les deux fonctions précédentes.
Déterminer les constantes d’intégration à partir des conditions initiales.

Autre études
A partir de la solution déterminée précédemment, on peut être amené à:

Tracer l’évolution temporelle.
Analyser un tracé temporel donné pour l’associer au système ou déterminer certaines caractéristiques (conditions initiales, régime forcé, type de régime pour un circuit d’ordre 2 - cf. suite - … )
Faire un bilan de puissance ou un bilan énergétique en déterminant la puissance reçue/fournie ou l’énergie reçue/fournie par les différents dipôles.
…

Méthode: Déterminer l’évolution temporelle.¶

Exercice

On redonne ci-dessous l’équation différentielle qui régit l’évolution de \(u_C\) ainsi que les conditions initiales. Déterminer \(u_C(t)\) pour t>0 en supposant \(R > \sqrt{\frac{L}{C}}\)

(43)¶\[\begin{equation} \frac{\rm{d^2}u_C}{\rm{dt^2}} + \frac{2}{RC} \frac{\rm{d}u_C}{\rm{dt}} + \frac{1}{LC} u_C = 0 \end{equation}\]

Conditions initiales: \(u_C(t=0^+) = 0\) et \(\frac{\rm{d}u_C}{\rm{dt}}(t=0^+) = -\frac{E}{RC}\)

Correction

Résolution de l’équation
On commence par chercher la solution de l’équation homogène. L’équation caractéristique est: \(r^2 + \frac{2}{RC} r + \frac{1}{LC} = 0\) soit comme solution:

(44)¶\[\begin{equation} r = -\frac{1}{RC} \pm j \sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} \end{equation}\]

La condition donnée dans l’énoncé implique un discriminant négatif, d’où l’utilisation des complexes. On rappelle qu’en physique \(j^2 = -1\)

Il vient la solution (on sépare les parties imaginaires et parties réelles) et l’on obtient directement la solution car il n’y a pas de second membre:

(45)¶\[\begin{equation} u_{C} (t) = {\exp}^{- \frac{t}{RC}} \left(A \cos \left(\sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} t \right) + B \sin \left(\sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} t \right)\right) \end{equation}\]

Il ne reste plus qu’à introduire les conditions initiales (Pour la seconde, on a déjà utilisé le fait que A = 0):

(46)¶\[\begin{align} u_{C} (t=0^+) &= A = 0\\ \frac{\rm{d}u_C}{\rm{dt}}(t=0^+) &= B \sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} = - \frac{E}{RC} \end{align}\]

Il vient:

(47)¶\[\begin{equation} u_{C} (t) = - \frac{E}{RC \sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}}} {\exp}^{- \frac{t}{RC}} \sin \left(\sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} t \right) \end{equation}\]

Vérification du résultat

Homogénéité: on doit vérifier plusieurs points: le facteur devant l’exponentielle doit être homogène à une tension et les deux facteurs dans l’exponentielle et le sinus doivent être homogène à des inverses de temps.

On peut utiliser le fait que RC est homogène à un temps (ce qu’on attend pour l’exponentielle) et LC homogène à un temps au carré. Il vient directement que l’argument de la racine est bien une somme de terme homogène à des \(s^{-2}\) donc la racine est homogène à des \(s^{-1}\) comme on l’attend dans le sinusoïde et au dénominateur du premier facteur (E est une tension, le dénominateur doit être sans dimension).

Sens physique: Il est important de vérifier: les conditions initiales et le nouveau régime forcé

Les conditions initiales correspondent bien à la valeur de la fonction et de sa dérivée à t=0.

Quand au nouveau régime forcé, on prend la limite à l’infini. On trouve bien 0.

Exemple d’autres études¶

Nous allons voir ici l’exemple d’autres études à partir soit de l’équation différentielle, soit de la forme temporelle. On rappelle qu’on peut aussi obtenir des information du circuit même (en régime forcé par exemple). Il est conseillé d’essayer de faire cet exercice avant de regarder la réponse.

Exercice

On rappelle que l’équation qui régit l’évolution de i(t) est:

(48)¶\[\begin{equation} \frac{\rm{d^2} i_l}{\rm{dt}^2} + \frac{2}{RC} \frac{\rm{d} i_l}{\rm{dt}} + \frac{1}{LC} i_l = -\frac{E}{RLC} \end{equation}\]

Conditions initiales: \(i_l(t=0^+) = 0\) et \(\frac{\rm{d}i_l}{\rm{dt}}(t=0^+) = 0\)

Déterminer \(i_l(t)\) dans l’hypothèse \(R > \sqrt{\frac{L}{C}}\).
En déduire la puissance reçue par le bobine p(t).
Déterminer l’énergie reçue par la bobine entre \(t=0\) et \(t=+\infty\).

Correction

Q1. Résolution de l’équation différentielle.
La solution générale de l’équation homogène est:

(49)¶\[\begin{equation} i_{l,0} (t) = {\exp}^{- \frac{t}{RC}} \left(A \cos \left(\sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} t \right) + B \sin \left(\sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} t \right)\right) \end{equation}\]

On cherche une solution particulière constante à l’équation avec second membre \(i_{L,1}(t) = I_0\). L’équation à résoudre (les dérivées temporelles s’annulent):

(50)¶\[\begin{equation} \frac{1}{LC} I_0 = - \frac{E}{RLC} \Longrightarrow I_0 = -\frac{E}{R} \end{equation}\]

La solution générale de l’équation avec second membre (identique à l’exercice précédent) est donc:

(51)¶\[\begin{equation} i_{l} (t) = {\exp}^{- \frac{t}{RC}} \left(A \cos \left(\sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} t \right) + B \sin \left(\sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} t \right)\right) - \frac{E}{R} \end{equation}\]

Les conditions initiales donnent le système d’équations:

(52)¶\[\begin{align} i_{l} (t=0^+) = A - \frac{E}{R} = 0 &\Longrightarrow A = \frac{E}{R}\\ \frac{\rm{d}i_l}{\rm{dt}} (t=0^+) = -\frac{E}{R^2C} + \sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} B = 0 &\Longrightarrow B = \frac{E}{R^2C\frac{1}{LC} - \frac{1}{{(RC)}^2}} \end{align}\]

On en déduit l’expression de l’intensité \(i_l(t)\) et de la tension \(u_L(t)\):

(53)¶\[\begin{align} i_{l} (t) &= {\exp}^{- \frac{t}{RC}} \left(\frac{E}{R} \cos \left(\sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} t \right) + \frac{E}{R^2C\sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}}} \sin \left(\sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} t \right)\right) - \frac{E}{R}\\ u_{L} (t) &= -\frac{EL}{R} {\exp}^{- \frac{t}{RC}} \left(\frac{1}{{(RC)}^2\sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}}} + \sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} \right) \sin \left(\sqrt{\frac{1}{LC} - \frac{1}{{(RC)}^2}} t \right) \end{align}\]

Vérification du résultat

S’entraîner comme précédemment à vérifier l’homogénéité du résultat et les informations physiques qu’on attend.

Attention

Erreur fréquentes

L’erreur fréquentes que les élèves font est de chercher les constantes d’intégration AVANT la solution particulière. C’est faux (ici on trouvera \(i_l(t) =0\) ce qui est évidemment incohérent).

Puissance reçue
Nous sommes en convention récepteur donc la puissance reçue est:

(54)¶\[\begin{align} p(t) &= i_{l}(t) \times u_L(t) \\ &= - L I_A^2 \left ({\exp}^{- \frac{2t}{\tau}} \left(\cos \left(\Omega t \right) + \frac{1}{\tau \Omega} \sin \left(\Omega t \right)\right)\left(\frac{1}{\tau^2 \Omega} + \Omega \right ) \sin \left(\Omega t \right) - \right )\\ & \times {\exp}^{- \frac{t}{\tau}} \left(\frac{1}{\tau^2 \Omega} + \Omega \right ) \sin \left(\Omega t \right) \end{align}\]

On a introduit les grandeurs suivantes : \(\tau = RC\) et \(\Omega =\sqrt{ \frac{1}{LC} - \frac{1}{{(RC)}^2}}\). Ce dernier terme est d’ailleurs très utilisé, on l’appelle la pseudo-période. Nous en reparlerons par la suite.

Variation d’énergie dans une bobine
Première méthode: intégrer l’expression précédente entre 0 et l’infini… … … On attendra pas un calcul aussi lourd (bien qu’il soit faisable et très formateur !).

Deuxième méthode (à appliquer) : Il faut se rappeler que l’énergie reçue par la bobine est stockée et qu’on connaît l’expression de cette énergie stockée. Ainsi, l’énergie reçue sera la différence entre l’énergie stockée au final et l’énergie stockée initialement.

(55)¶\[\begin{equation} \Delta E_L = E_L(t=+\infty) - E_L(t=0) = \frac{1}{2}L I(t=\infty)^2 - \frac{1}{2}L I(t=0)^2 = \frac{L E^2}{2R^2} \end{equation}\]

Analyse des formes des solutions¶

Rappel des expressions
On rappelle les expressions trouvées pour la tension aux bornes du condensateur et pour l’intensité circulant dans la bobine. On pourra pour élargir encore les observations calculer les autres grandeurs du circuits.

Seconde différence
Une seconde différence concerne les constantes d’intégration (en vert). Elles vont aussi dépendre de l’état initial (en plus de toutes les dépendances citées précédemment).

Remarquons que ce sont les seules grandeurs qui vont garder trace du l’état initial: ni la forme de la solution générale ESSM, ni le régime forcé ne va dépendre de l’état initial. Ce sont les grandeurs qui donnent le moins d’information sur le comportement général du système.

Electrocinétique

Méthodes d’analyse d’un régime transitoire¶

Mise en équation¶

Méthode: Déterminer l’équation différentielle (Lois de Kirchhoff)¶

Méthode: Déterminer l’équation différentielle (utilisation des potentiels)¶

Remarques sur les équation différentielles obtenues¶

Détermination des conditions initiales¶

Combien de condition initiales¶

Continuité des grandeurs¶

Méthode: Déterminer des conditions initiales¶

Etude de l’évolution temporelle¶

Etude de l’évolution temporelle¶

Méthode: Déterminer l’évolution temporelle.¶

Exemple d’autres études¶

Analyse des formes des solutions¶