Filtre: définition et caractéristiques¶
Filtrage: Principe¶
Quadrupôle
Un quadripôle est un composant qui présente 2 bornes d’entrée et 2 bornes de sortie.
Définition : Fonction de transfert/Filtre
On définit la fonction de transfert \(\underline{H}(j \omega) = \frac{\underline{s}}{\underline{e}}\) comme le rapport des amplitudes complexes des tensions d’entrée \(e\) et de sortie \(s\) en régime sinusoïdal forcé de pulsation \(\omega\) quand la sortie est ouverte.
Un filtre est un quadripôle dont la fonction de transfert dépend explicitement de la pulsation \(\omega\).

Remarque
Une fonction de transfert n’a de sens que si le système est stable et linéaire.
Si la condition de linéarité est indispensable, il arrive d’étudier un système en régime sinusoïdal forcé pour ensuite vérifier sa stabilité.
Exercice Exemples de filtres
On peut construire un filtre artificiellement pour de multiples usages.
Un système mécanique est commandé par un signal électrique. Ce système mécanique est censé fonctionner à des fréquences comprises entre 0 et 10Hz. De plus, au dessus de 100Hz, les vibrations rapides du systèmes peuvent endommager l’appareil. On se propose donc de créer un filtre passe-bas coupant les fréquence supérieures à 10Hz.
Le secteur délivre une tension dont les fréquences sont autour de 50Hz (à 2 Hz) près. Pour éviter des parasites gênant dans le son délivré par un haut-parleur, on désire “couper” les fréquences comprises entre 45Hz et 55Hz.
Certains systèmes peuvent avoir des effets de filtrages non désirés ou naturels:
Un pont soumis au vent est un système mécanique réagissant différemment à des excitations périodiques de fréquences différentes. Il arrive ainsi qu’ils possèdent une fréquence de résonance à laquelle ils vont vibrer plus fortement (pont de Tacoma).
Les atomes et molécules soumis à un rayonnement électromagnétiques réagissent différemment suivant la fréquence du rayonnement: au maximum de vibration, il absorbent un maximum d’énergie. C’est la base des analyses de spectre (IR, UV… )
Caractéristiques générales d’un filtre¶
Important
Définition : Gain réel, argument et gain en décibel
Les caractéristiques d’un filtre sont:
son module \(G = \frac{s_m}{e_m}\), appelé gain réel: il correspond au rapport des amplitudes réelles
sa argument ou phase: il va correspondre au déphasage que va avoir la sortie sur l’entrée.
son gain en décibel défini par \(G_{db} = 20 \log \frac{s_m}{e_m}\) (attention: c’est une grandeur réelle): on verra que c’est une manière plus pratique de se représenter le rôle et l’efficacité d’un filtre.
Remarque
Intensité en sortie
Par convention, la fonction de transfert d’un filtre est toujours calculée avec une intensité sortant du filtre nulle.
Il faut noter que si dans les conditions d’utilisation l’intensité en sortie n’est pas nulle, cela peut modifier le comportement du filtre. (cf. suite)

Types de filtres¶
Les filtres sont de différents types suivant leur finalité. Nous ne présentons ici que les types de filtres les plus utilisés (et ceux que vous devez connaître). Dans le cadre du programme, on peut associer à chaque type de filtre des comportements haute et basse fréquence précis. C’est en étudiant ces comportements qu’on déterminera le type de filtre.
Important
Fondamental : Types de filtres
les filtres dit passe-bas: leur but est de laisser passer les basses fréquences et de couper les hautes fréquences. Normalement, on utilise ces filtres pour laisser passer une gamme de fréquence jusqu’à une fréquence voulue (qu’on appellera fréquence de coupure) et couper les fréquence plus rapides.
On reconnaît les filtres passe-bas par un comportement basse fréquence non-nul et un comportement haute-fréquence nul.
les filtres dit passe-haut: leur but est de laisser passer les hautes fréquences et de couper les basses fréquences. Normalement, on utilise ces filtres pour laisser passer une gamme de fréquence à partir une fréquence voulue (qu’on appellera fréquence de coupure) et couper les fréquence plus lentes.
On reconnaît les filtres passe-haut par un comportement basse fréquence nul et un comportement haute-fréquence non-nul.
les filtres dit passe-bande: leur but est de laisser passer une bande de fréquence entre deux fréquences choisies (qui sont appelées fréquences de coupure).
On reconnaît les filtres passe-bande par un comportement basse fréquence et un comportement haute-fréquence nul.
les filtres dit coupe-bande (ou réjecteur de bande): leur but est de couper une bande de fréquence entre deux fréquences choisies (qui sont appelées fréquences de coupure).
On reconnaît les filtres coupe-bande par un comportement basse fréquence et un comportement haute-fréquence non-nul et égaux. Il existe (et surtout) aussi une fréquence pour laquelle le gain s’annule.
Exemple
Utilisation d’un filtre passe-bas: On peut s’en servir pour extraire une valeur moyenne ou pour filtrer les parasites d’un signal (quand ils sont haute-fréquence).
Utilisation d’un filtre passe-haut: On peut l’utiliser pour supprimer une valeur moyenne. Le mode AC de l’oscilloscope (et du multimètre) utilise un filtre passe-haut sur la voie où le mode est choisi.
Utilisation d’un filtre passe-bande: Comme on le signalait en introduction, elle peuvent être utilisée en acoustique pour “découper” le son en plusieurs bandes de fréquence qu’on va amplifier de manière différentes. Les filtres passe-bande sont aussi utilisée en analyse spectrale, pour la sélection des radios…
Utilisation d’un filtre coupe-bande: L’exemple donné en introduction: quand on veut supprimer la fréquence 50Hz du secteur qui peut bruiter un signal.
Filtres idéaux
Pour comprendre le principe d’un filtre, nous allons partir sur des exemples de filtres “idéaux” tel qu’on voudrait les concevoir. Un filtre idéal est en général basé sur le principe du “tout-ou-rien”. On laisse passer la fréquence, ou on la coupe.
En théorie, on essaie d’avoir un filtre idéal, c’est-à-dire laissant passer les fréquences dans une gamme de fréquence voulue avec un gain constant et avoir un gain nul pour les fréquences qu’on veut filtrer. On donne ci-dessous l’allure du gain des filtres idéaux correspondants aux filtres usuels cités ci-dessous : (a) filtre passe-bas, (b) filtre passe-haut, (c) filtre passe-bande, (d) filtre coupe-bande.
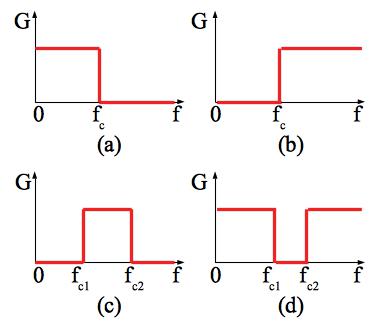
Le problème est qu’on ne peut en pratique réaliser de tels filtres (d’où le nom… ). C’est pourquoi, on va créer des filtres qui se rapprochent plus ou moins du comportement idéal. Nous allons voir comment étudier de tels filtres.
Diagramme de Bode¶
Important
Définition : Diagramme de Bode
Le diagramme de Bode est la représentation graphique utilisée pour les filtres linéaires. Il consiste à représenter le gain en décibel et la phase du filtre en fonction de \(\log(\omega)\).
Remarque
Pulsation réduite
Pour l’étude d’un filtre linéaire, on peut souvent faire apparaître une grandeur \(\omega_0\) homogène à une pulsation telle qu’on pour en comparant la pulsation d’excitation \(\omega\) à cette pulsation différencier les faibles pulsations (faibles fréquences) des fortes pulsations (fortes fréquences). On appelle cette grandeur une pulsation propre. On définit alors la pulsation réduite: \(x= \frac{\omega}{\omega_0}\).
Lorsqu’on trace des diagrammes de Bode théoriques, on les trace souvent en fonction de \(\log(x)\) au lieu de \(\log(\omega)\).
Décade
Une décade est un intervalle de pulsation \([\omega_1;\omega_2]\) (ou de pulsation réduite \([x_1;x_2]\), ou encore de fréquence \([f_2;f_2]\)) tel que \(\frac{\omega_2}{\omega_1}=\frac{x_2}{x_1}=\frac{f_2}{f_1} = 10\). Autrement dit, quand on avance d’une décade, on multiplie par dix la pulsation.
Sur un diagramme de Bode, une décade correspond à un écart \(\Delta(\log(x)) = 1\).
Remarque
Diagramme semi-logarithmique
En général, on représente les diagrammes de Bode sur des papier semi-log qui représentent les valeurs de x (ou de \(\omega\)) en absisses et non \(\log(x)\).
Méthode: Etude d’un filtre¶
Exercice
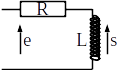
Déterminer le type de filtre par une étude haute et basse fréquence.
Déterminer la fonction de transfert du filtre et en déduire son gain réel, son gain en décibel, sa phase. On introduira la pulsation propre \(\omega _0\) telle que:
On veut tracer le diagramme de Bode. Montrer que:
Le gain réel est strictement croissant
Il est maximal à haute fréquence. Préciser sa valeur.
La fonction \(G_{dB}(\log(x))\) possède une asymptote oblique en \(\log(x) \to - \infty\) de pente \( + 20 \rm{dB/decade}\).
La phase est strictement décroissante. On déterminera ses valeurs asymptotiques.
Correction
Type de filtre
A basse fréquence la bobine est assimilable à un fil, la tension s est donc nulle.
A haute fréquence, la bobine se comporte comme un interrupteur ouvert. L’intensité circulant dans la résistance est donc nulle et la tension à ses bornes aussi. Il vient (loi des mailles) que s = e.
Le filtre a une fonction de transfert nulle à basse fréquence et non nulle à haute fréquence. C’est un filtre passe-haut.
Fonction de transfert
La bobine et la résistance forment un pont diviseur de tension. La tension aux bornes de la bobine est donc:
Il vient que la pulsation propre est \(\omega_0 = \frac{R}{L}\).
Il vient que les caractéristiques du filtre sont:
Diagramme de Bode
Le gain réel se met sous la forme \(G = \frac{1}{\sqrt{1 + \frac{1}{x^2}}}\). Il vient immédiatement que le gain réel est strictement croissant.
On en déduit la fonction atteint son maximum en \(x = + \infty\). Le gain réel vaut alors 1 et le gain en décibel vaut 0. Il vient que le diagramme de Bode possède une asymptote horizontale \(G_{dBa,asymp}= 0\) en \(x \to + \infty\) (en \(\omega \to + \infty\), c’est-à-dire à haute fréquence).
A très basse fréquence (\(\omega \to 0 \Longrightarrow x \to 0 \Longrightarrow \log x \to - \infty\)), le gain réel se réécrit \(G \approx x\) soit un gain en décibel \(G_{dB} \approx 20 \log x\). Le gain en décibel s’appproche donc d’une droite en fonction de \(\log(x)\) de pente +20. Le gain en décibel s’exprime en… décibel et l’abscisse \(\log(x)\) se compte en décade. Le gain en décibel possède donc, sur un diagramme de Bode une asymptote oblique à basse fréquence de pente \(+20 \rm{dB/decade}\).
La fonction arctan étant croissante, la phase est décroissante. Ses valeurs limites sont \(\pi/2\) et 0.
On peut donc tracer le diagramme de Bode:
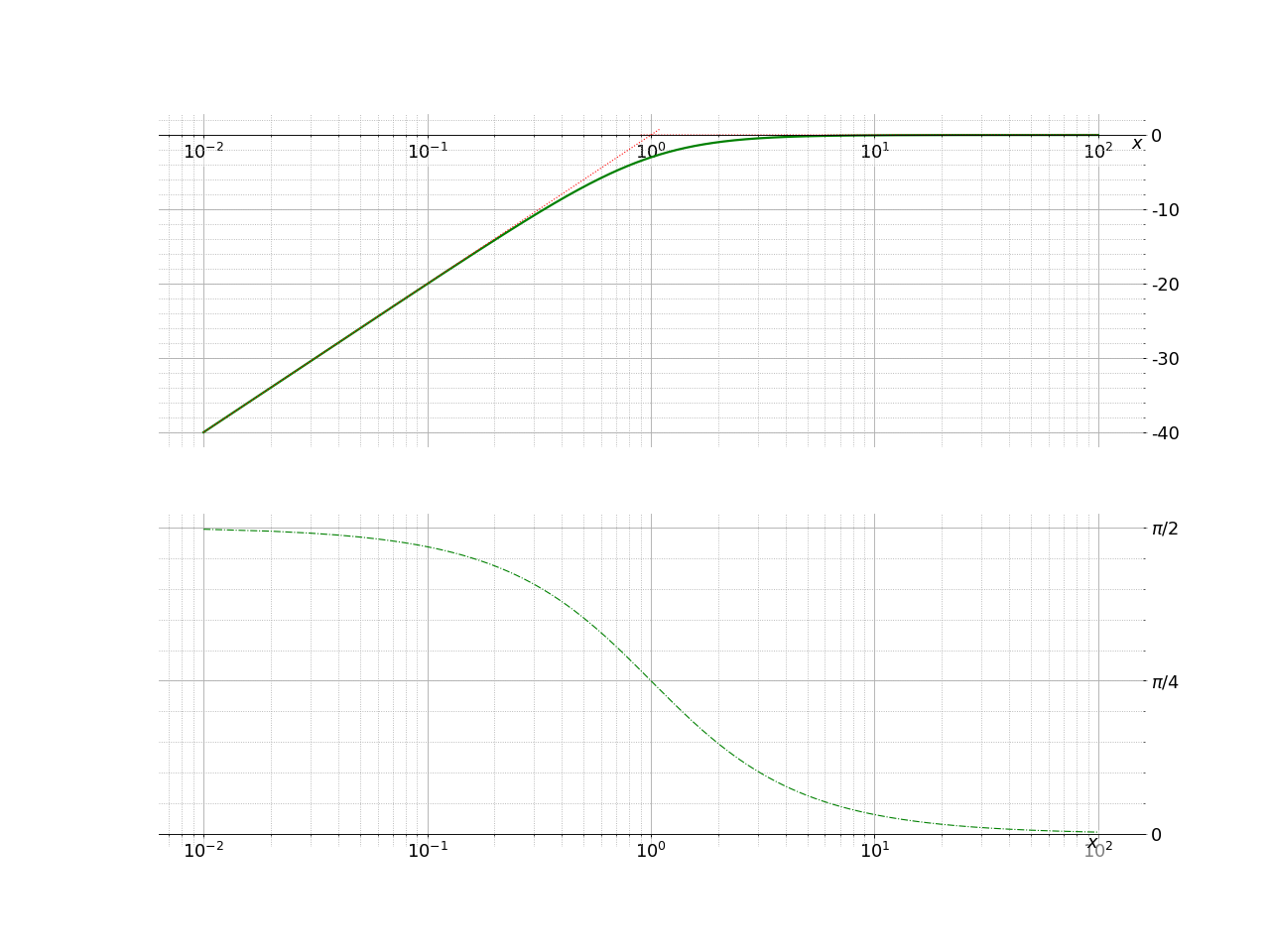
Etude fréquentielle d’un filtre: Bilan¶
Bilan
Etudier un filtre permet de prévoir son comportement face à une réponse quelconque (cf. suite) mais aussi de choisir les composants pour réaliser tel ou tel type de filtrage. Lors d’une étude fréquentielle d’un filtre peut:
Déterminer le type de filtre, soit par une étude des limites de la fonction de transfert, soit par une étude rapide du circuit à haute et basse fréquence.
Déterminer la fonction de transfert. On peut alors déterminer la phase du filtre ainsi que son gain réel.
Etudier le gain réel pour déterminer le comportement du filtre (résonance, bande passante, type, ordre… )
Tracer le diagramme de Bode pour pouvoir retrouver/obtenir les caractéristiques précédentes. On peut aussi y figurer le comportements asymptotiques (sous forme d’asymptotes horizontales ou obliques). Nous verrons que cette étude asymptotique peut être très utile pour étudier la réponse d’un filtre.