Régime transitoire et régime forcé¶
Comme tout système physique, un circuit électrique répond aux contraintes qu’on lui impose de l’extérieur. En général, cette contrainte est une tension d’entrée qui peut soit être créée volontairement avec une forme particulière, soit provenir d’un capteur de mesure.
Dans tous les cas, le circuit va finir par se placer dans un état qu’on appellera régime forcé par le régime d’entrée.
Lorsqu’un système est dans un régime forcé et qu’une perturbation se produit en entrée (modification de la tension envoyée par le capteur ou modification volontaire de la grandeur d’entrée), le système va évoluer vers un nouveau régime forcé. L’évolution entre le premier et le second régime forcé est appelé régime transitoire.
Il est en général important de pouvoir distinguer le régime transitoire du régime forcé, de pouvoir analyser les caractéristiques du régime transitoire, de pouvoir déterminer quel sera le prochain régime forcé…
Régimes de fonctionnement: régime transitoire et régime forcé¶
Préambule: Système stable
Un système est dit stable si les grandeurs du système ne divergent pas lorsqu’il est laissé à lui-même.
Un système instable tend à saturer ou à se détériorer. Nous supposerons ici que nos systèmes sont toujours stables et nous verrons par la suite des méthodes pour vérifier la stabilité d’un système.
Important
Définition : Régime forcé
Lorsqu’un système stable est soumis à une grandeur d’entrée, les grandeurs du systèmes vont tendre vers un état dépendant:
du système lui-même et de la grandeur considérée
de la grandeur d’entrée.
En général, la forme mathématique des grandeurs du système tend à prendre une forme similaire à la forme mathématique de la grandeur d’entrée. On parle alors de régime forcé.
Exercice Exemples de régimes forcés
Si la grandeur d’entrée est une tension constante, alors toutes les grandeurs d’un système stable vont tendre vers une valeur constante. Dans ce chapitre, nous nous limiterons principalement à ce type de régime forcé.
Si la grandeur d’entrée est une tension sinusoïdale, alors toutes les grandeurs d’un système stable vont tendre vers une forme sinusoïdale de même pulsation. Ce sera l’objet du prochain chapitre.
Important
Définition : Régime transitoire
Lorsque la grandeur d’entrée varie brusquement pour passer d’une forme à une autre, le système (ses grandeurs) va évoluer durant un temps fini (non nul) pour tendre (s’il est stable) vers un nouveau régime forcé par la nouvelle grandeur d’entrée.
L’évolution entre le régime forcé précédent et le nouveau régime forcé est appelé régime transitoire.
Exercice Repérer les régimes sur une évolution temporelle
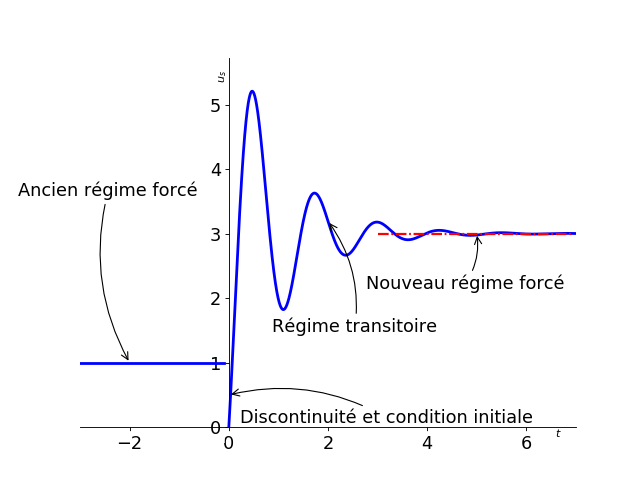
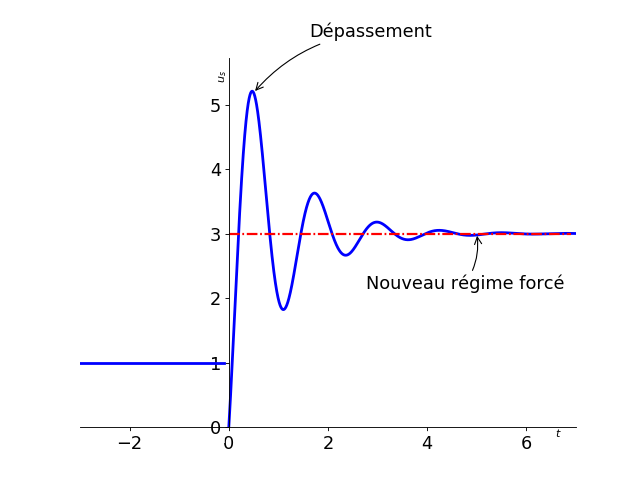
On observe sur le graphique précédent (la tension \(u_s\) est une des grandeurs du système) les différents régimes lors de l’évolution d’un système. Notons plusieurs points importants:
On remarque une discontinuité qui correspond au moment où la grandeur d’entrée change brusquement de valeur. La présence possible de discontinuité impose la recherche de conditions initiales (valeurs à \(t = 0^+\)) pour pouvoir résoudre les équations mises en jeu (des équations différentielles).
En général, on atteint pas mathématiquement le nouveau régime forcé car le régime transitoire est un fonction qui tend vers 0: elle ne s’annule pas rigoureusement à un moment donné.
Il faut donc un critère (temps de réponse) pour décider quand l’écart au nouveau régime forcé est négligeable: ce sera le moment où l’on considère le régime transitoire comme fini. Le critère choisi dépend des besoins en précision du système par exemple. Nous verrons par la suite que l’on peut déterminer un ordre de grandeur de cette durée qu’on appellera temps caractéristique.
Etude d’un circuit en régime forcé indépendant du temps¶
Nous allons étudier le cas du régime forcé indépendant du temps. Il s’agit là de l’un des deux types de régime forcé que nous étudierons cette année. On parlera aussi de régime permanent indépendant du temps.
Dans ce régime, toutes les grandeurs ne varient plus au cours du temps.
Condensateur et bobine en régime indépendant du temps¶
Important
Fondamental : Condensateur en régime indépendant du temps
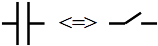
En régime indépendant du temps, un condensateur est équivalent à un interrupteur ouvert.
Démonstration
Comme étudié dans le chapitre précédent, remarquons qu’en régime indépendant du temps, la dérivée de la tension est nulle. Il vient:
L’intensité étant toujours nulle, le dipôle est assimilable à un interrupteur ouvert.
Important
Fondamental : Bobine en régime indépendant du temps
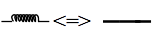
En régime indépendant du temps, une bobine est équivalent à un fil.
Démonstration
Comme étudié dans le chapitre précédent, remarquons qu’en régime indépendant du temps, la dérivée de l’intensité est nulle. Il vient:
La tension étant toujours nulle, le dipôle est assimilable à un fil.
Etude d’un circuit en régime indépendant du temps
Les deux propriétés précédentes permettent d’étudier les circuits en régime forcé indépendant du temps. Il suffit de remplacer les condensateurs et bobines par des interrupteurs ouverts et par des fils puis d’étudier le circuit avec les règles des chapitres précédents.
Méthode : étude d’un régime indépendant du temps.¶
Cette exercice explique la méthode d’étude d’un régime indépendant du temps
Exercice
Étudier le circuit suivant en régime indépendant du temps lorsque l’interrupteur est ouvert. On déterminera toutes les intensités.
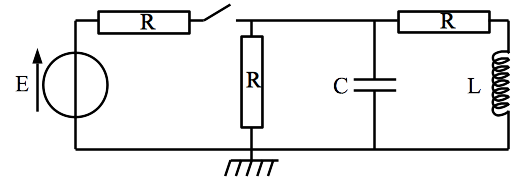
Correction
Mise en équation
On oriente toutes les intensités vers le haut dans chaque branche et on note respectivement \(i_e, i_r, i_c, i_l\) les intensités qui circulent dans la source, la résistance seule dans sa branche, le condensateur, la bobine.
Dessiner le circuit équivalent en régime indépendant du temps
Tout d’abord, on redessine le circuit en utilisant les modèles équivalents au condensateur et à la bobine en régime indépendant du temps.
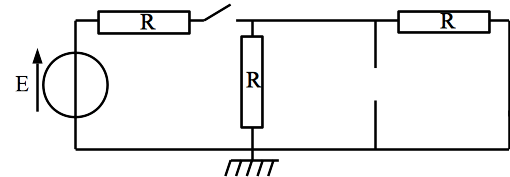
Il suffit ensuite d’étudier le circuit. Il vient directement \(i_e = i_c = 0\) à cause des interrupteurs ovuerts.
On a donc \(i_r + i_l = 0\) et \(R i_r - R i_l = 0\) soit \(i_l = i_r = 0\)
Remarquons que seules deux tensions sont non nulles: la tension de la source (E) et la tension aux bornes de l’interrupteur de gauche (E ou -E suivant l’orientation).
Attention
Tension aux bornes d’un condensateur
Profitons de cette remarque pour signaler que la tension aux bornes d’un interrupteur ouvert n’est a priori pas nulle.
Exercice
Etudier le circuit précédent en régime indépendant du temps lorsque l’interrupteur est fermé. On déterminera toutes les intensités.
Correction
Tout d’abord, on redessine le circuit en utilisant les modèles équivalents au condensateur et à la bobine en régime indépendant du temps.
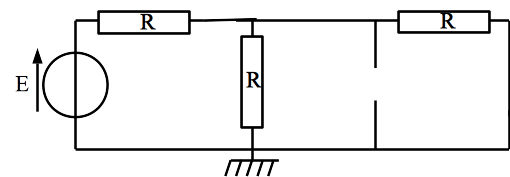
Il suffit ensuite d’étudier le circuit. Il vient directement \(i_c = 0\) à cause des interrupteurs ouverts.
Écrivons les lois de Kirchhoff (on pourrait aussi utiliser la loi des noeuds en terme de potentiels):
Il vient immédiatement \(i_r = i_l\) et donc \(i_e = - 2 i_r\). La première loi des mailles s’écrivant alors \(E + 3 R i_R = 0\), il vient:
Analyse des résultats
Homogénéité: Les intensités sont bien homogènes à des tensions sur des résistances.
Sens physique: Assez logiquement l’intensité \(i_e\) est positive (si E est positive car elle dans le sens de E) tandis que les deux autres sont négatives (sens inverse de E).
On a un pont diviseur de courant avec deux résistances identiques, on trouve logiquement l’égalité des intensités \(i_l = i_r\) et le fait que l’intensité \(i_e\) est le double des deux autres.
Généralités sur les caractéristiques des régimes transitoires¶
Etudier un régime transitoire: la réponse indicielle¶
Réponse indicielle
Comme nous le verrons par la suite, le régime transitoire d’un système possède:
des caractéristiques qui dépendent du contexte extérieur (tension d’entrée) et de la grandeur considérée
des caractéristiques qui dépendent de l’état initial du système
des caractéristiques qui ne dépendant que du circuit considéré
Un manière d’étudier un système et notamment de déterminer ces caractéristiques propres au système est d’étudier sa réponse indicielle, c’est-à-dire sa réponse à un échelon de tension.
Echelon de tension
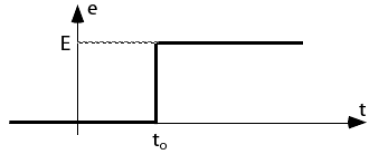
Un échelon de tension est un passage brusque d’une tension \(E_0\) à une tension \(E_1\).
Un échelon de tension permet de simuler une brusque variation de la tension d’entrée.
Très souvent les échelons étudiés correspondent à un passage de 0 à E.
Attention
Discontinuité
Un échelon de tension introduit une discontinuité à un instant t (\(t=0\) ou \(t=t_0\) plus généralement). Celà signifie qu’en ce point, les grandeurs physiques ne sont plus nécessairement continues.
A l’image des traitements mathématiques, cela nécessite de traiter chaque partie (avant et après la discontinuité séparément) et de procéder à des recollements. Nous verrons les méthodes d’études propres à la physique par la suite. __Il faut néanmoins déjà retenir qu’on ne peut écrire a priori \(u(t=t_0^-) = u (t=t_0^+)\) pour n’importe quelle grandeur du circuit __s’il y a une discontinuité du circuit imposée.
Nous verrons que certaines (deux) grandeurs sont toujours continues par propriétés fondamentales.
Simulation d’un échelon de tension
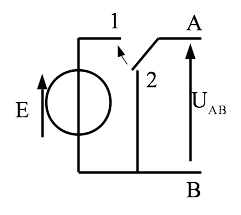
Pour simuler un échelon de tension, on utilise très souvent une source E (pile par exemple) et un interrupteur 3 points.
Le basculement de l’interrupteur de 2 vers 1 permet de simuler un échelon.
A l’inverse le basculement de 1 et vers 2 simule un régime libre, c’est-à-dire un régime dans lequel toutes les sources sont éteintes.
Remarque
Simulation en entrée
Nous simulons ici l’entrée par un passage d’une valeur constante à une autre valeur constante. Nous étudions donc la réponse indicielle. Cette dernière est particulièrement adaptée à l’étude du régime transitoire.
Il faut noter qu’on peut simuler d’autres entrées. Nous verrons par exemple dans le prochain chapitre l’analyse fréquentielle basée sur la simulation d’une entrée sinusoïdale. Dans ce cas, on s’intéresse moins au régime transitoire mais beaucoup plus au régime forcé qu’on finit par obtenir.
Caractéristique d’un régime transitoire: dépassement¶
Dépassement
Si le régime forcé visé est un régime indépendant du temps, on peut s’intéresse à l’existence ou l’absence de dépassement, c’est-à-dire regarder si le signal va dépasser la valeur finale.
En physique, savoir repérer graphiquement l’existence d’un dépassement est suffisant.
Intérêt
Dans certains cas les dépassements ne sont pas souhaitables car ils peuvent détériorer le système.
Rapidité d’un système: temps caractéristique et temps de réponse¶
Rapidité d’un système
On considère qu’un système est rapide s’il atteint rapidement (!) le nouveau régime permanent après que la perturbation s’est produite…
En pratique, les équations mathématiques prévoit qu’on atteint rigoureusement le nouveau régime permanent que lorsque t tend vers l’infini (nous verrons que des exponentielles tendant vers 0 interviennent dans nos systèmes).
On s’intéresse donc au moment où l’écart au régime permanent reste suffisamment faible.
On distinguera deux types de temps pour caractériser la rapidité d’un système:
les temps de réponse basés sur des définitions précises.
les temps caractéristiques donnant un ordre de grandeur de la rapidité du système.
Temps de réponse
Un temps de réponse à N% est l’écart de temps entre l’instant de la perturbation et l’instant à l’écart entre le signal étudié et le nouveau régime permanent va rester inférieur à (100-N)% de l’écart initial entre le signal et le nouveau régime permanent.
Remarque: Cette définition n’est pas à connaître, d’autant qu’il faut l’adapter à des cas où la grandeur dans l’état initial et l’état final a la même valeur. Vous pouvez être amener à calculer de tels temps si on vous donne la définition.
Remarque: les temps de réponses les plus utilisés sont les temps de réponse à 95% et à 99%.
Remarque
Du temps de réponse au temps caractéristique
L’inconvénient du temps de réponse est qu’il peut dépendre des conditions initiales et aussi du pourcentage choisi. Néanmoins, les études montrent que pour un système donné, les temps de réponses ont toujours le même ordre de grandeur quelque soient les conditions initiales ou le pourcentage choisi (nous le verrons sur un exemple).
On peut alors, à partir des équations mathématiques, exhiber une grandeur homogène à un temps qu’on appellera temps caractéristique et qui donnera cet ordre de grandeur du temps de réponse du système.
Remarque: nous verrons sur des exemples concrets comment déterminer un temps caractéristique et comment celui-ci peut-être relié à un temps de réponse.
Etude du temps de réponse sur une évolution temporelle.¶
On se propose de déterminer graphiquement un temps de réponse à 95% sur le graphique suivant:
Exercice
Déterminer le temps de réponse à 95% pour le signal dont l’évolution est représentée ci-dessous.
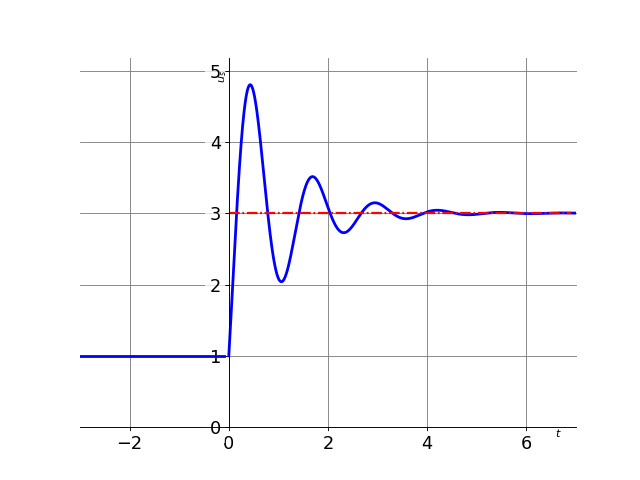
Correction
Détermination du temps de réponse
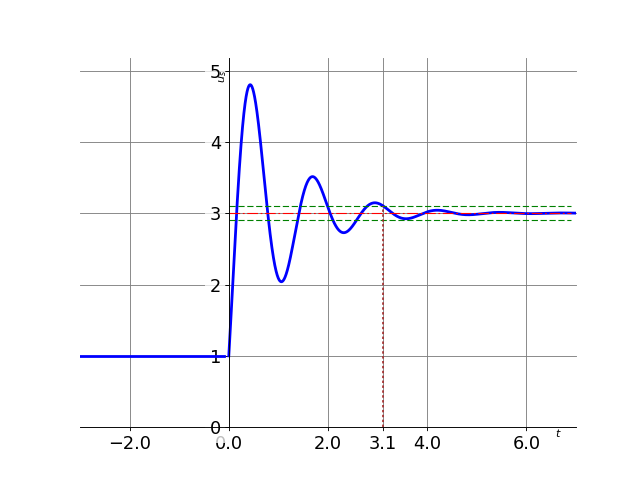
On détermine dans un premier temps l’écart initial: on commence à 1V et on finit à 3V. L’écart de 5% est donc de \((3 - 1 ) * 0.05 \% = 0.1V\) on regarde donc quand l’écart entre le signal et la valeur finale reste inférieur à 0.1V soit compris 2.9V et 3.1V
L’instant correspond est de 3.1s. La perturbation arrivant à 0s, le temps de réponse est de 3.1s
Méthode : Détermination d’un temps caractéristique¶
Exercice
On considère le signal ci-après.
\begin{enumerate}
Déterminer le temps de réponse à N%. L’exprimer pour N=95 puis pour N=99
En déduire un temps donnant l’ordre de grandeur du temps caractéristique pour une exponentielle décroissante.
Correction
1.
La valeur initiale est \(e_m\) et la valeur finale 0. On cherche donc un écart à la valeur finale de \(\frac{N}{100}(e_m - 0)\) soit :
Pour 95%, on trouve \(t = 3 \tau\) etpour 99%, on trouve \(t = 5 \tau\).
Important
Fondamental : 2. Temps caractéristique d’une exponentielle décroissante
On voit que le temps caractéristique est toujours de l’ordre de \(\tau\). __Lorsqu’on est en présence d’une exponentielle décroissante de la forme \(\exp(-t/\tau\), on prendra comme temps caractéristique : \(\tau\). C’est pour des temps grands devant \(\tau\) que l’argument de l’exponentielle devient proche de \(-\infty\) et donc que l’exponentielle devient proche de 0.
Exercice
On considère le signal suivant:
Déterminer une estimation du temps caractéristique après avoir préciser l’état final.
Correction
Ecart à l’état final
Le régime forcé s’obtient en passant simplement à la limite l’expression du signal. Il vient \(u_{s,force} = 3e_m\)
L’écart est donc:
L’écart initial étant de \(2 e_m\), il faut analyser la fonction:
Remarque
Cas du temps de réponse
Pour un temps de réponse à 95%, c’est la fonction f(t) précédente qu’il faudrait utiliser pour déterminer l’instant à partir duquel \(f(t) < 0.05\) tout le temps.
De telles études analytiquement seront réalisées dans des cas plus simples, la résolution de ce cas étant hors-programme (on pourrait - dans une exercice conjoint informatique-physique - essayer de réaliser une analyse numérique pour déterminer ce temps caractéristique).
Rappel : Pour une exponentielle seule \(\exp^{-t/\tau}\), le temps caractéristique au bout duquel on peut considérer qu’elle est négligeable devant 1 est \(\tau\)
Temps caractéristique du signal considéré.
Ici, il y a deux exponentielles décroissantes (si elles sont croissantes, le système diverge et il n’y a pas de temps caractéristique mais un système instable !).
On va donc considérer que l’écart devient négligeable lorsque les deux exponentielles sont négligeables.
Et le temps caractéristique du système complet sera gouverné par l’exponentielle la plus lente donc celle qui possède le temps caractéristique le plus long.
Ici la première exponentielle possède un temps caractéristique T/2 et la seconde un temps caractéristique T/5. La première est la plus lente et le temps caractéristique du signal total est donc T/2.
Remarque
Étude rapide
Remarquons que toute la première partie permettant de ramener la fonction à un écart relatif à l’état final est en réalité superflu pour la recherche d’un temps caractéristique. L’étude des facteurs de dilatation des exponentielles suffit.
Etude d’un portrait de phase¶
Nous avons jusqu’à présent étudier les évolutions graphiquement au moyen des évolutions temporelles. On peut obtenir d’autres informations en utilisant une représentation particulière appelée portrait de phase.
Portrait de phase¶
Important
Définition : Portrait de phase
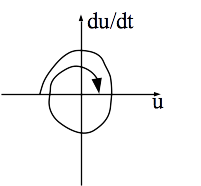
Un portrait de phase est la représentation de la dérivée de la grandeur \(\dot u(t)\)en ordonnée en fonction de la grandeur \(u(t)\). C’est un tracé orienté (temporellement).
On trace par exemple i en fonction de q pour un condensateur. On parle du portrait de phase du condensateur.
Quelques fois, on représente l’intensité en fonction de la tension et l’on parle aussi de portrait de phase lorsque l’intensité est proportiionnelle à la dérivée de la tension (condensateur).