TD Electrocinétique 3: Régimes de fonctionnements¶
Circuit d’ordre 1¶
Exercice
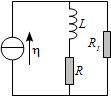
Calculer i, l’intensité qui circule dans la bobine. On donne \(i(t=0)=0\).
En déduire \(i_1\) et \(u_1\) (tension aux bornes de \(R_1\) et courant circulant dans \(R_1\)).
Tracer i et \(i_1\) en fonction du temps.
Eléments de réponse (sans justification)
\(i(t) = \frac{R_1}{R_1 + R}\eta\left ( 1 - e^{- \frac{(R_1 + R)t}{L}}\right )\)
Deux condensateurs¶
Exercice
On considère le circuit électrique de la figure ci-après. A t=0, \(q_1 = Q_1\) et \(q_2 = 0\). Donner l’évolution ultérieure (tensions et intensité) et faire un bilan énergétique.
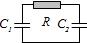
Eléments de réponse (sans justification)
\(q_1(t) = Q_1 \frac{C_1}{C_1 + C_2} + Q_1 \frac{C_2}{C_1 + C_2}e^{-\frac{(C_1 + C_2)t}{RC_1 C_2}}\)
L’énergie stockée dans les deux condensateurs a globalement diminuée: elle correspond à l’énergie dissipée dans la résistance.
Circuit soumis à une rampe.¶
Exercice
On branche en parallèle une bobine d’inductance \(L=10 \rm{mH}\) (non parcourue par un courant avant t=0), une résistance \(R = 1 \rm{k \Omega}\) et un générateur idéal de courant qui fournit une rampe de courant \(\eta\) de pente \(\lambda\) en partant de 0A et jusqu’à un courant \(I_0 = 1 \rm{A}\) (atteint pour un temps \(t_0\)) puis reste constant.
Établir l’équation d’évolution de \(i(t)\) le courant qui traverse la bobine quand le générateur débite une rampe de courant. Que vaut \(i(0^{+})\)?
Pour \(t < t_0\), chercher une solution particulière sous la forme \(i_O(t) = \alpha t + \beta\). En déduire \(i(t)\) pour \(t < t_0\) de l’équation.
Calculer \(t_0\) en fonction de \(\lambda\) et \(I_0\). Discuter suivant les valeur de \(\lambda\) et \(I_0\) les parts relatives données au régime transitoire et au régime “permanent” — on définira ces deux régimes.
On prend \(\lambda = 1 \rm{A.s^{-1}}\), quelle approximation peut-on faire? Que vaut \(i(t_0)\)? En déduire l’évolution de \(i(t)\) après \(t=t_0\).
Calculer l’énergie délivrée par le générateur pendant les deux périodes \(\left[0;t_0\right]\) et \(\left[t_0;+\infty\right]\). La comparer avec l’énergie délivrée par un générateur délivrant un échelon de courant \(I_0\) branché en parallèle à R et L. Commenter.
Eléments de réponse (sans justification)
Toutes les intensités sont orientées vers le bas.
\(\frac{\rm{d}i}{\rm{dt}} + \frac{R}{L} i = \eta\).
\(i(t) = \lambda (t - \tau) + \lambda \tau e^{-t/tau}\)
On doit comparer \(t_0\) à \(\tau\).
On peut considérer l’exponentielle négligeable dans la condition initiale en \(t = t_0\). \(i(t > 0) \approx I_0 - \lambda \tau e^{\frac{t_0 - t}{\tau}}\)
L’énergie trouvée est deux fois moins importante.
Oscillateur faiblement amorti¶
Exercice
On considère un circuit RLC série en régime libre. A \(t=0\), l’intensité circulant dans le circuit est \(I_0\) et la tension aux bornes du condensateur et nulle.
On suppose de plus que \(RC \ll \frac{L}{R}\).
Préciser le type de régime pour le système.
Dans l’approximation proposée, simplifier l’expression de la pseudo-pulsation.
Comparer le temps caractéristique du réigme transitoire et la pseudo-période du signal. En déduire l’allure graphique de q(t).
Déterminer l’expression complète de q(t).
Eléménts de réponse (sans justification)
C’est un régime pseudo-périodique et la pseudo-pulsation est à peu près égale à la pulsation propre. Le temps caractéristique \(\frac{2Q}{\omega_0}\) est donc grand devant la pseudo-période (Q grand) donc on observe de nombreuses oscillations et une enveloppe exponentielle qui décroit lentement.
Protection d’un interrupteur¶
Exercice
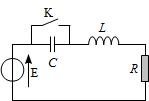
Dans le circuit ci-dessous, l’interrupteur K est fermé et à t=0, on l’ouvre.
Expliciter la tension \(u(t)\) aux bornes de K dans le cas où \(L/R>>RC\).
On donne \(L = 10 \rm{mH}, E = 5 \rm{V}, R = 50 \rm{\Omega}\). Évaluer la valeur maximale de \(u(t)\) en l’absence du condensateur (l’interrupteur a alors une propre capacité de 10pF). On attend de l’initiative dans les calculs.
Justifier l’emploi d’un condensateur. Déterminer la valeur de celui-ci pour limiter la valeur maximale de \(u(t)\) à 500V.
Eléments de réponse (sans justification)
\(u(t) \approx e^{\frac{-\omega_0 t}{2Q}} (- E \cos(\omega_0 t) + QE\sin \omega_0 t) + E\) (à fort facteur de qualité, on doit trouver que la pseudo-pulsation égale la pulsation propre en première approximation).
\(u_{\max} \approx QE\) La tension obtenue est très grande: risque d’arc électrique. Le condensateur en parallèle augmente la valeur de C et diminue la surtension.