Contents

Réponse d’un filtre linéaire

Nous allons étudier ici les différents méthodes pour obtenir la réponse d’un filtre à une entrée donnée. Nous verrons qu’à nouveau on utilise le principe de linéarité. Après avoir étudié la réponse exacte d’un filtre nous verrons que souvent l’étude de réponses approchées donne des informations suffisantes. Nous verrons deux types d’étude: l’assimilation à un filtre idéal et l’assimilation aux comportement asymptotique

Méthode: Réponse d’un filtre à un sinusoïde

Exercice

On reprend le filtre précédent dont la fonction de transfert est \(\underline{H} = \frac{jx}{1 + jx}\) avec \(x = \frac{\omega}{\omega_0}\) et \(\omega_0 = \frac{R}{L}\).

  1. Nous allons commencer par établir la réponse exacte du filtre.

    1. Exprimer le signal de sortie \(s(t)\) pour un signal d’entrée sinusoïdal de pulsation \(\omega\) et d’amplitude \(e_m\).

    2. On considère un signal d’entrée \(e(t) = e_1 \cos \omega_1 t + e_2 \cos \omega_2 t\) avec \(\omega_1 = 0.1 \omega_0\) et \(\omega_2 = 10 \omega_0\). Exprimer la réponse exacte du filtre.

  2. Nous allons maintenant assimiler la réponse du filtre à sa version idéale.

    1. Pour des fréquences faibles devant \(\omega_0\), simplifier l’expression du gain et de la phase à l’ordre 0.

    2. Pour des fréquences hautes devant \(\omega_0\), simplifier l’expression du gain et de la phase à l’ordre 0.

    3. On considère un signal d’entrée \(e(t) = e_1 \cos \omega_1 t + e_2 \cos \omega_2 t\) avec \(\omega_1 = 0.1 \omega_0\) et \(\omega_2 = 10 \omega_0\). Dans le cadre d’approximation par un filtre idéal, exprimer la tension de sortie.

    4. Comparer graphiquement les représentations graphiques de la réponse exacte et de la réponse “tout-ou-rien” qui vient d’être établie.

  3. Nous allons maintenant assimiler la réponse du filtre à ses comportements asymptotiques établies lors du tracé du diagramme de Bode.

    1. A basse fréquence, on rappelle qu’on a montré que la fonction de transfert peut se réécrire \(\underline{H} = j x\). En déduire la relation temporelle entrée-sortie à basse-fréquence. Comment se comporte le filtre pour un signal dont le spectre est entièrement inférieur à la bande fréquence \(\omega_0\) ?

Correction

Réponse exacte

\[\begin{align*} s(t) &= \frac{e_m \frac{\omega}{\omega_0}}{\sqrt{1 + {\left(\frac{\omega}{\omega_0}\right)}^2}}\cos \left(\omega t + \frac{\pi}{2} - \arctan \frac{\omega}{\omega_0}\right)\\ s(t) &= \frac{0.1 e_1}{\sqrt{1.01}}\cos \left(0.1 \omega_0 t + \frac{\pi}{2} - \arctan 0.1\right) + \frac{10 e_1}{\sqrt{101}}\cos \left(10 \omega_0 t + \frac{\pi}{2} - \arctan 10\right) \end{align*}\]

Réponse idéale
A basse fréquence, la fonction de transfert est se résume à \(\underline{H} = 0\) d’où un gain de 0 et à haute fréquence, elle se résume à \(\underline{H} = 1\) d’où un gain de 1.

Dans le cadre d’approximation par un filtre idéal, on va associer le gain maximal aux fréquences conservées (ici les hautes fréquences, c’est un filtre passe haut) et un gain nul pour les autres (ici les basses fréquences). A haute fréquence la phase est aussi quasi nulle. Il vient donc que: \(s(t) = e_2 \cos \left ( 100 \omega_0 t \right )\).

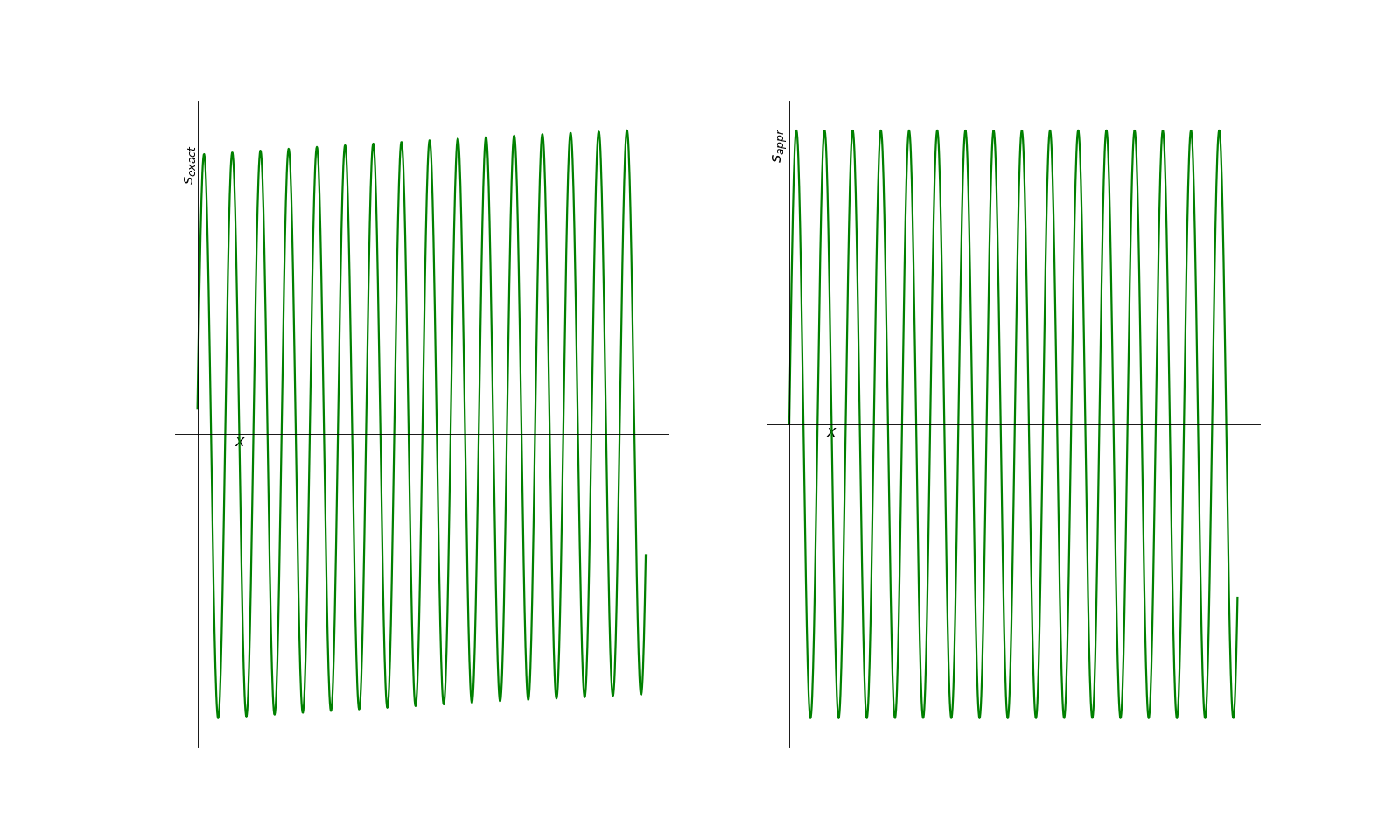
On a représenté ci-dessous la réponse exacte (gauche) et la réponse approchée (droite).On observe que les signaux sont à peu près identiques. L’utilisation du modèle idéal est ici plutôt valable car les fréquences sont suffisamment loin de la fréquence propre pour que la fonction de transfert soit proche de sa valeur limite HF et BF.

../_images/filtre_rl_somme.png

Réponse asymptotique
A basse fréquence, la relation se réécrite \(\underline{s} = \frac{j \omega}{\omega_0} \underline{e}\) soit en temporel \(s(t) = \frac{1}{\omega_0}\frac{\rm{d}e}{\rm{dt}}(t)\). Pour les basses fréquences, le filtre se comporte comme un dérivateur. (On parlera de pseudo-dérivateur car il ne se comporte comme dérivateur que pour une partie du spectre).

Cas d’un signal d’entrée périodique

Exercice

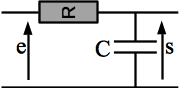
On considère le filtre ci-dessous.

  1. Déterminer rapidement le type de filtre puis la fonction de transfert. En déduire le gain réel et la phase. On mettra la fonction de transfert sous la forme \(\underline{H} = \frac{A}{1 + j x}\) avec x la pulsation réduite.

  2. Justifier que le gain réel est strictement décroissant. Montrer que la représentation du gain en décibel sur un diagramme de Bode \(G_{dB}(\log(x))\) admet une asymptote oblique à haute fréquence de pente \(- 20 \rm{dB/decade}\)

  3. On définit la bande passante du filtre comme la gamme de fréquence où le gain réel est supérieur au gain maximal divisé par \(\sqrt{2}\). Déterminer la bande passante.

../_images/elec_rc_passe_bas.jpg
Correction

A basse fréquence, le condensateur se comportant comme un interrupteur ouvert, il impose une intensité nulle. La loi des mailles donne donc s = e. A haute fréquence, le condensateur se comportant comme un fil, il vient s=0. Il s’agit donc d’un filtre passe-haut.

La résistance et le condensateur forment un pont diviseur de tension (on rappelle qu’on étudie le filtre avec une intensité sortante nulle) donc: \(\underline{s} = \frac{1}{1 + j RC \omega} \underline{e}\). Il vient une pulsation propre \(\omega_0 = \frac{1}{RC}\).

Le gain réel est donc \(G = \frac{1}{\sqrt{1 + x^2}}\) et la phase \(\phi = - \arctan x\)

La décroissance du gain réel est triviale. A haute fréquence, la fonction de transfert devient \(\underline{H} \approx \frac{1}{jx}\) soit un gain en décibel \(G_{dB} \approx -20 \log x\). Il vient bien une pente de \(- 20 \rm{dB/decade}\).

../_images/filtre_rc_bode.png

Le gain réel étant strictement décroissant, le gain maximal est le gain à fréquence nulle (gain statique) soit ici 1. On cherche donc à résoudre l’inégalité:

(108)\[\begin{equation} \frac{1}{\sqrt{1 + x^2}} \geq \frac{1}{\sqrt{2}} \Longrightarrow x\leq 1 \Longrightarrow \omega \leq \omega_0 \end{equation}\]

Remarque: La (les) pulsation(s) réalisant l’égalité sont les limites de la bande passante, on les appelle les pulsations de coupure. Ici, la pulsation de coupure égale la pulsation propre. Ce n’est pas une généralité.

Exercice

On considère le filtre précédent et on envoie en entrée un signal créneau d’amplitude E. On admet que la décomposition spectrale du signal créneau est:

(109)\[\begin{equation} e(t) =\frac{4E}{\pi} \sum\limits_{k=0}^{\infty}\frac{\sin \left((2k+1)2\pi f t\right)}{2k+1} \end{equation}\]

  1. Donner la réponse exacte du filtre pour une fréquence du créneau \(f = f_0\) avec \(f_0\) la fréquence propre associée à la pulsation propre.

  2. Donner une réponse approchée du filtre en assimilant sa réponse à celle d’un filtre idéal lorsque \(f = f_0/2\).

  3. Déduire de la fonction de transfert la relation temporelle entrée-sortie à haute fréquence. Quel comportement possède le filtre dans ce domaine spectral ? En déduire une réponse approchée du filtre en utilisant ses comportements asympotiques lorsque \(f = 10 f_0\)

Correction

Réponse exacte

(110)\[\begin{equation} s(t) =\frac{4E}{\pi} \sum\limits_{k=0}^{\infty}\frac{1}{\sqrt{1 + {\left(2k+1\right)}^2}} \frac{\sin \left((2k+1)2\pi f t - \arctan (2k+1) \right)}{2k+1} \end{equation}\]

Réponse idéale
Nous avons trouver que la bande passante correspond aux fréquences inférieures à \(f_0\). Dans un filtre idéal, le gain dans la bande passante serait le gain maximale soit ici 1. Hors de la bande passante, ce serait un gain nul. Pour \(f = f_0/2\), seul le fondamental de fréquence \(f_0/2\) est dans la bande passante, la fréquence de l’harmonique suivant étant \(3f_0/2\). Il vient que le signal de sortie approché se résume à \(s(t) \approx \frac{4E}{\pi} \sin\left (\pi f_0 t\right )\)

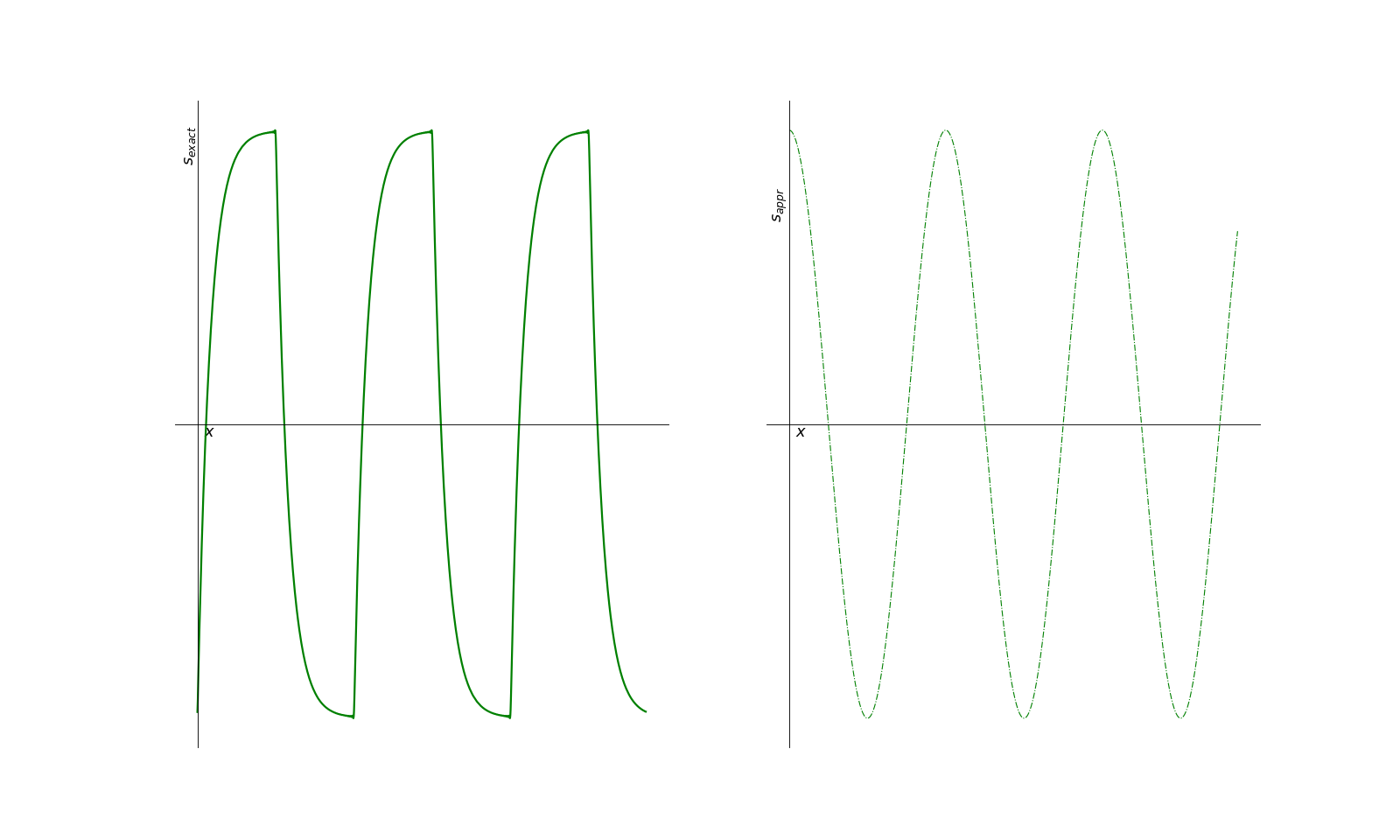
On représente ci-dessous la réponse exacte (gauche) calculée pour le même signal et la réponse approchée (droite).On remarque que l’utilisation du modèle idéal n’est PAS valable ici. Celà vient du fait qu’un filtre d’ordre 1 n’attenue pas suffisamment les composantes hors de la bande passante qui son proche de la pulsation de coupure: elle influent donc sur l’allure du signal. Cela n’invalide pas l’étude demanière approchée dans le cas général. Nous l’utiliserons souvent mais il faut garder à l’esprit que pour des fréquences trop proches du passage passant-filtré et pour des ordres de filtre faible, cette approximation peut s’écarter de la réponse exacte.

../_images/filtre_rc_exact_app.png

Réponse asymptotique
La fonction de transfert à haute fréquence s’écrit \(\underline{H} \approx \frac{1}{j \frac{\omega}{\omega_0}}\) soit en temporelle \(s(t) = \omega_0 \int e(t)\). Le filtre se comporte à haute fréquence comme un intégrateur (on parlera de pseudo-intégrateur car il n’intègre pas tout le signal).

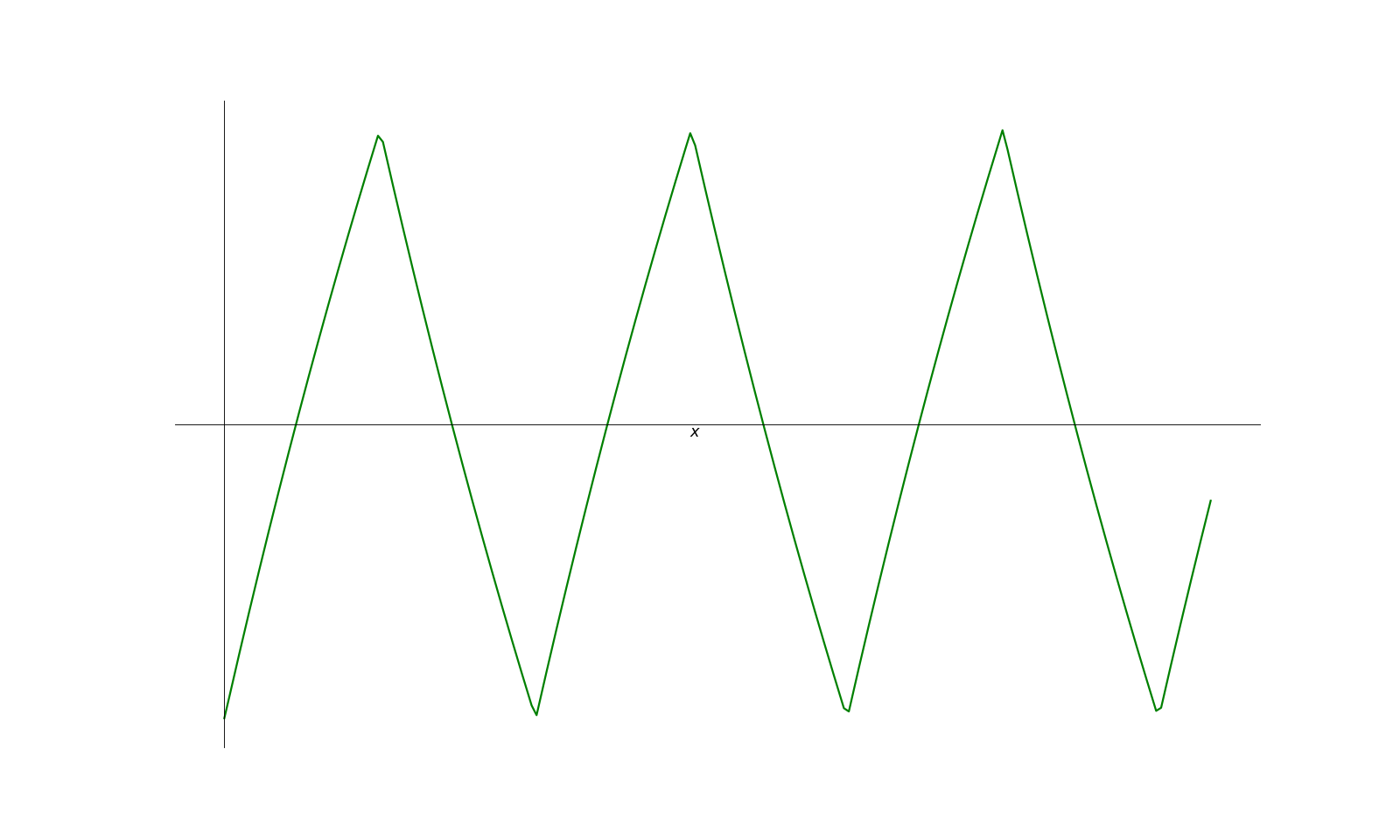
Le créneau que l’on envoie possède tout son spectre dans la partie intégrée. Il vient que le signal est intégré. Celà donnera en sortie un signal triangulaire (intégration de parties constantes).

On représente ci-dessous la réponse exacte. On observe qu’effectivement le signal est intégré. La qualité de l’approximation tient du fait qu’une approximation par les asymptotes est plus fine qu’une approximation “tout ou rien” et que les fréquences sont suffisamment éloignées de la fréquence propre pour être considérées comme haute fréquence.

../_images/filtre_rc_integ.png

Méthode: Analyse d’un diagramme de Bode

Exercice

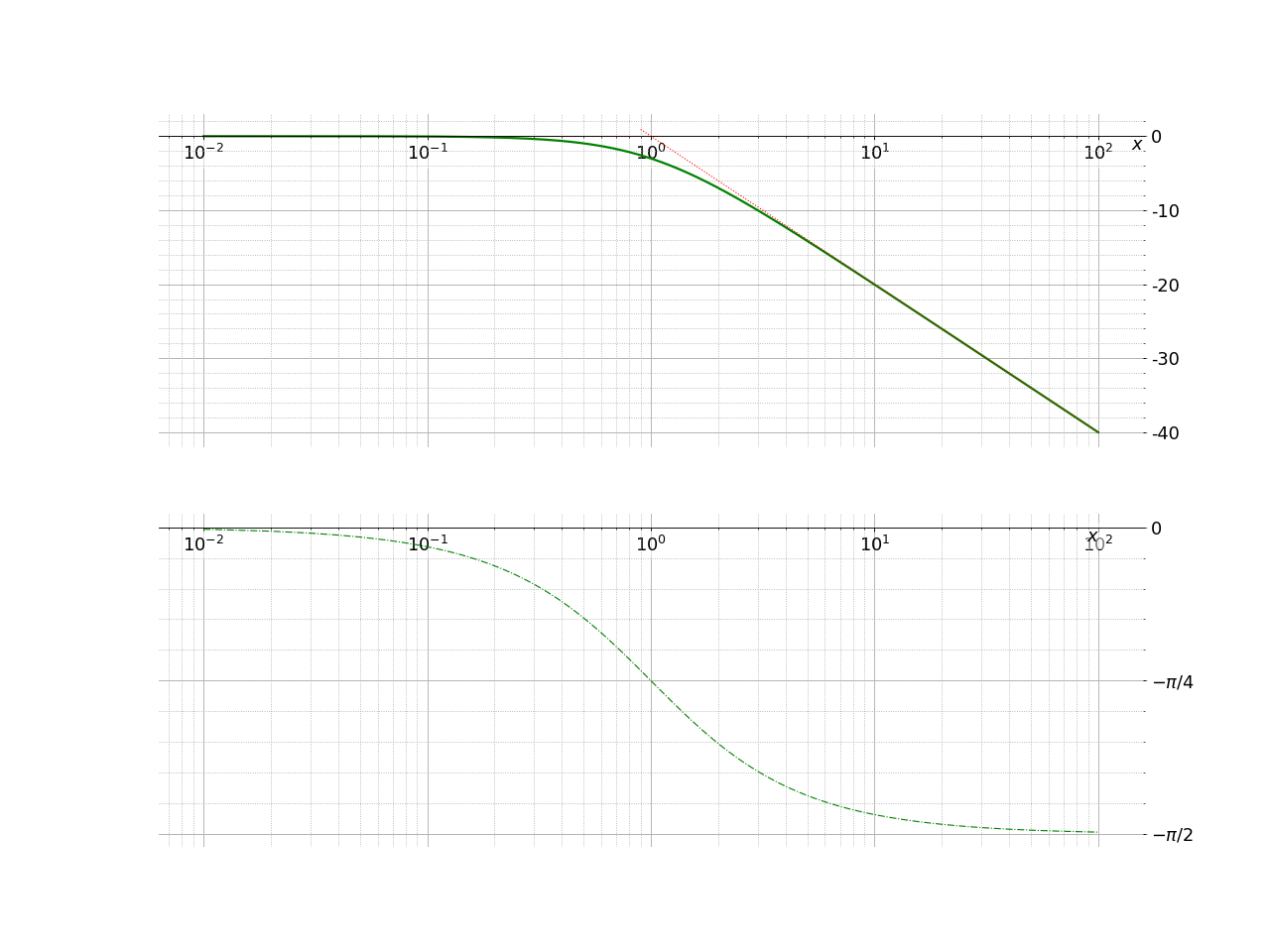
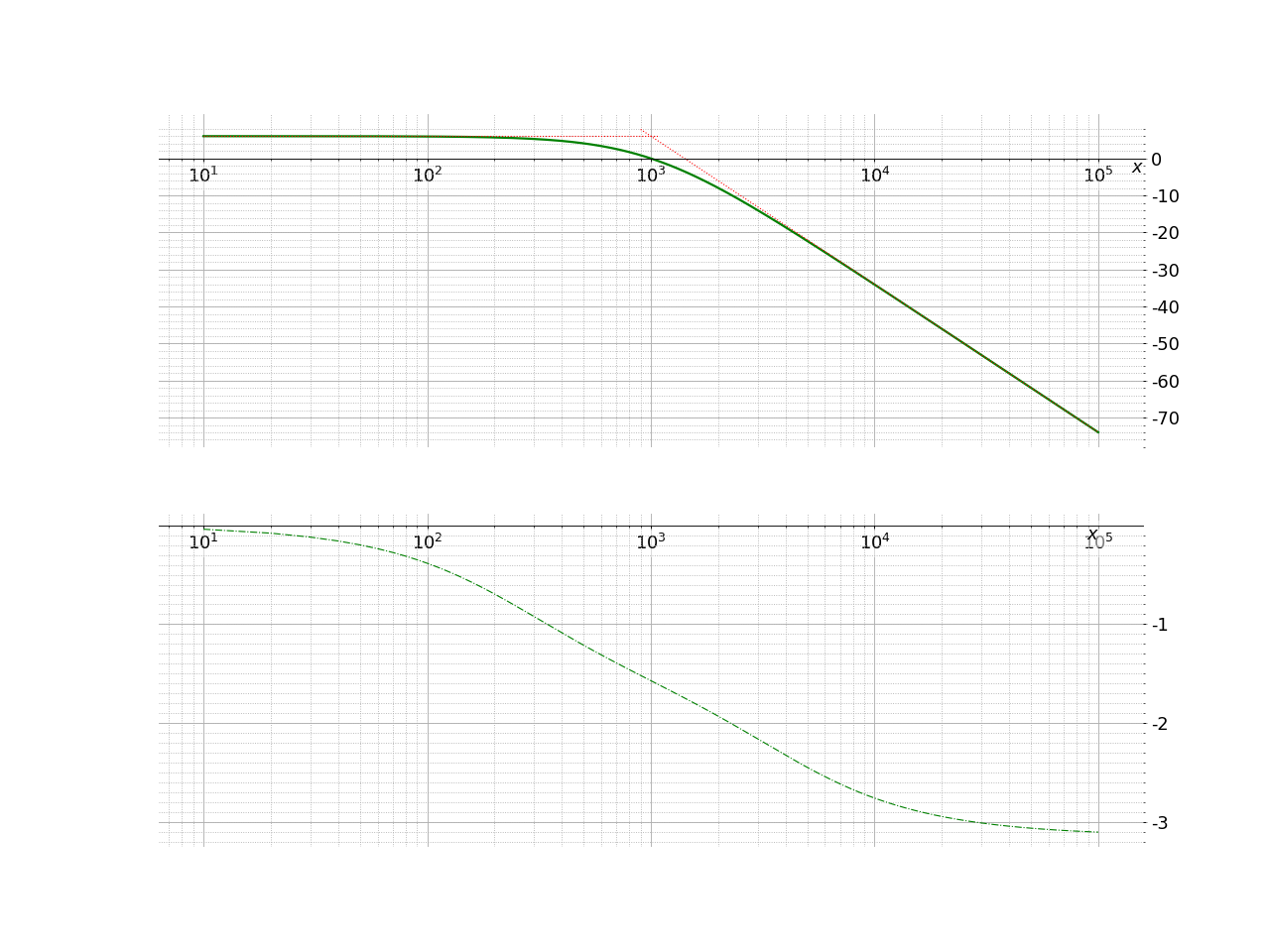
On considère un filtre dont le diagramme de Bode (tracé en fonction de \(\log(\omega)\))est donné ci-après.

  1. Préciser le type de filtre.

  2. On peut déterminer graphiquement la pulsation propre de deux manières: elle se trouve à l’intersection des asymptotes haute et basse fréquence du filtre et pour ce filtre, la phase à la pulsation propre vaut \(- \pi/2\). Déterminer la pulsation propre par les deux méthodes et vérifier la cohérence des deux résultats.

  3. Déterminer l’équation de l’asymptote oblique à la représentation \(G_{dB}(log(\omega))\) sur le diagramme de Bode en gain. En déduire, dans cette zone la relation temporelle approchée entre la sortie et l’entrée.

  4. On définit une fréquence de coupure comme une fréquence pour laquelle le gain est égal au gain maximal divisé par \(\sqrt{2}\). Déterminer numériquement la valeur de la pulsation de coupure.

../_images/filtre_graphique_bode.png
Correction

Le gain en décibel est non nul à basse fréquence (quand \(\log(x)\) tend vers \(-\infty\)) et nul à haute fréquence (le gain en décibel tend vers \(-\infty\)). Il s’agit donc d’un filtre passe-haut.

On trouve \(\omega_0 \approx 10^3 \rm{rad.s^{-1}}.\)

On trouve une pente de \(-40dB/decade\). L’ordonnée pour \(\log(\omega) = \log(\omega_0)\) est 6. L’équation de l’asymptote est donc \(Asymp(\log(\omega)) = 6 - 40 \log(\omega/\omega_0)\). On peut remarquer que la phase est presque égale à \(-\pi\). On peut donc considérer que la fonction de transfert est un réel négatif soit: \(\underline{H} \approx - \frac{2}{{(\frac{\omega}{\omega_0})}^2}\). En temporelle, celà donne: \(s(t) = 2 \omega_0^2 \int (\int (e(t)))\): c’est un comportement double intégrateur.

On veut un gain réel égal à \(G_{\max}/\sqrt{2}\) soit un gain en décibel égal à \(G_{dB,\max} - 3dB\) soit 3dB. On trouve \(\omega_c = 6 * 10 ^ 2 \rm{rad.s^{-1}}\).

Remarque

Voici un exemple où la pulsation propre et la pulsation de coupure ne sont pas égales.

Les graduations données ici correspondent à un diagramme semi-logarithmique, c’est-à-dire que les graduations correspondent à x et non à \(\log(x)\).

previous

Filtre: définition et caractéristiques

next

Caractéristiques générales