.ipynb .md .pdf

Binder

Contents

Méthode d’étude d’un régime sinusoïdal forcé

Représentation complexe des signaux sinusoïdaux

Comme nous allons le voir, l’étude d’un régime sinusoïdal forcé est largement simplifiée par l’introduction des grandeurs complexes et plus précisément des représentations complexes des signaux sinusoïdaux. Nous allons commencer par définir ces grandeurs et voir leur propriétés.

Représentation complexe d’un signal sinusoïdal

Définition : Représentation complexe d’un signal sinusoïdal

Considérons un signal sinusoïdal de la forme \(s(t) = s_m \cos (\omega t + \varphi)\). On définit la représentation complexe \(\underline s(t)\) du signal \(s(t)\) par la grandeur:

(88)\[\begin{equation} \underline{s}(t) = s_m \exp j\left(\omega t + \varphi\right) \end{equation}\]

On définit aussi l’amplitude complexe \(\underline{s_m}\) du signal \(s(t)\) par la grandeur:

(89)\[\begin{equation} \underline{s}(t) = s_m \exp \left(j \varphi\right) = \frac{\underline{s}(t)}{\exp j \omega t} \end{equation}\]

Important

Fondamental : Relation complexe-réel

On a les relations suivantes:

\[\begin{align*} \textrm{Grandeurs réelle :} &s(t) = \Re \left (\underline{s(t)} \right) \\ \textrm{Amplitude (réelle) :} &s_m = \left\vert \underline{s_m} \right\vert = \left\vert \underline{s(t)} \right\vert \\ \textrm{Phase à l'origine :} &\varphi = \arg(\underline{s_m}) \end{align*}\]

Ces relations sont fondamentales car elles permettent de déduire les caractéristiques (amplitude et phase à l’origine) du signal réel (ce qui nous intéresse au final) connaissant la grandeurs complexes associées (ce qu’on déterminera en premier).

Opérations sur les grandeurs complexes

Important

Fondamental : Combinaison linéaire

La représentation complexe de la combinaison linéaire de deux signaux de même pulsation est égale à la même combinaison linéaire des représentations complexes de deux mêmes signaux:

(90)\[\begin{equation} s = \lambda_1 s_1 + \lambda_2 s_2 \Longrightarrow \underline{s} = \lambda_1 \underline{s_1} + \lambda_2 \underline{s_2} \textrm{ avec } (\lambda_1;\lambda_2) \in \mathbb{R}^2 \end{equation}\]

Important

Fondamental : Dérivation et intégration

La représentation complexe de la dérivée d’un signal sinusoïdal de pulsation \(\omega\) est égale à la représentation complexe du même signal sinusoïdal multiplié par \(j \omega\):

(91)\[\begin{equation} \underline{\frac{\rm{d}s}{\rm{dt}}} = j \omega \underline{s} \end{equation}\]

La représentation complexe de la primitive - de valeur moyenne nulle - d’un signal sinusoïdal de pulsation \(\omega\) est égale à la représentation complexe du même signal sinusoïdal divisé par \(j \omega\):

(92)\[\begin{equation} \underline{\int_s dt} = \frac{\underline{s}}{j \omega} \end{equation}\]

Démonstration (pour l’intégration)
On pose \(u(t) = A \cos \omega t + \phi\)

\[\begin{align*} \int u(t)dt &= \frac{A \sin(\omega t + \phi)}{\omega} = \frac{A \cos(\omega t + \phi - \frac{\pi}{2})}{\omega}\\ &\textrm{soit:}\\ \underline{\int u(t)dt} &= \frac{A e^{j(\omega t + \phi - \frac{\pi}{2})}}{\omega} = \frac{A}{j \omega} e^{j(\omega t + \phi)} = \frac{\underline{u}}{j \omega} \end{align*}\]

Ces dernières relations sont très utiles car nous allons pouvoir transformer l’étude d’équations différentielles en étude de polynômes.

Intérêt des grandeurs complexes

Nous allons voir à travers l’étude du cas présenté précédemment l’intérêt de la grandeur complexe. Essayer de le résoudre avec les grandeurs réelles (on rappelle qu’on sait que le régime forcé est un régime sinusoïdal de même pulsation que l’entrée) puis passer à la correction pour voir l’utilisation des complexes.

Exercice

On rappelle qu’on étudie le circuit ci-après. Le point qui reste à prouver est l’étude fréquentielle, c’est-à-dire l’étude du régime sinusoïdal forcé par un sinusoïde quelconque de pulsation \(\omega\). On rappelle que le but est prouver que la tension aux bornes du condensateur pour une entrée de la forme \(e(t) = e_m \cos \omega t\)est de la forme:

(93)\[\begin{equation} \frac{e_m}{\sqrt{1 + {\left(RC \omega\right)}^2}} \cos\left(\omega t - \arctan \left(RC \omega\right) \right) \end{equation}\]

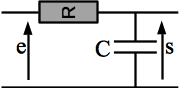
Correction

Méthode 1: Passer l’équation différentielle en représentation complexe
Nous verrons par la suite qu’on peut directement étudier le circuit au moyen des représentations complexes. Pour l’instant, nous allons voir une première méthode, pas la plus efficace mais déjà plus performante que de rester avec les grandeurs réelles. Les méthodes plus directes seront présentées par la suite.

1. Obtention de l’équation différentielle: une loi des mailles en utilisant \(u_R = Ri = RC \frac{\rm{d}s}{\rm{dt}}\) donne: \(RC \frac{\rm{d}s}{\rm{dt}} + s = e\)

2. Passage aux grandeurs complexes: l’égalité des représentations complexes implique l’égalité de leurs parties réelles. On va donc prendre la représentation complexe de chaque terme de l’équation différentielle en gardant l’égalité. Résoudre cette égalité donnera une grandeur complexe dans la partie réelle est la solution cherchée. On va donc résoudre l’équation: \(\underline{RC \frac{\rm{d}s}{\rm{dt}} + s} = \underline{e}\), \(\underline{e}\) étant la représentation complexe de e, elle a pour expression \(e_m \exp j \omega t\). Remarquons au passage qu’on a ici choisit l’origine des phases pour l’ensemble du système: c’est la tension d’entrée.

3. Utilisation des propriétés des représentations complexes: on utilise les propriétés de linéarité et de la dérivée. L’équation se réécrit: \(j RC \omega \underline{s} + \underline{s} = \underline{e}\)

4. Résolution complexe: On obtient \(\underline{s} = \frac{\underline{e}}{1 + j RC \omega}\)

5. Passage aux grandeurs réelle: On obtient l’amplitude du signal en prenant le module de la représentation complexe: \(s_m = \frac{e_m}{\sqrt{1 + {(RC \omega)}^2}}\).

6. Passage à la grandeur réelle: On obtient la phase à l’origine en prenant l’argument de la représentation complexe: \(\varphi = - \arctan RC \omega\).

7. Passage à la grandeur réelle: La solution est donc: \(s(t) = \frac{e_m}{\sqrt{1 + {(RC \omega)}^2}} \cos (\omega t - \arctan RC \omega)\)

Remarque

Phase à l’origine et déphasage
On a pris comme “origine des phases”, c’est-à-dire comme signal dont la phase à l’origine est nulle le signal d’entrée. C’est une pratique très fréquente (on ne peut le faire qu’avec un seul signal). Dès lors la phase à l’origine des autres grandeur (ici s) correspond au déphasage de cette grandeur par rapport à la tension d’entrée.

Non-méthode: Utilisation des réelles.
Insistons sur le fait que cette méthode n’est PAS à utiliser. Elle est présentée ici pour montrer que la résolution avec les complexes est plus simple.

On cherche un régime forcé sous la forme \(s(t) = s_m \cos \omega t + \varphi\). On l’introduit dans l’équation différentielle, ce qui donne:

(94)\[\begin{equation} - RC \omega s_m \sin (\omega t + \varphi) + s_m \cos \omega t + \varphi = e_m \cos \omega t \end{equation}\]

soit en linéarisant:

(95)\[\begin{equation} s_m \left(- RC \omega \cos \varphi - \sin \varphi\right) \sin \omega t + s_m \left(\omega \cos \varphi - RC \sin \varphi\right) \cos \omega t = e_m \cos \omega t \end{equation}\]

L’égalité étant vraie pour tout t, il vient que les coefficients devant chaque sinus et cosinus doivent être les mêmes:

\[\begin{align*} &\begin{cases} s_m \left(- RC \omega \cos \varphi - \sin \varphi\right) &= 0\\ s_m \left(\omega \cos \varphi - RC \omega \sin \varphi\right) &= e_m \end{cases}\\ &\Longrightarrow \\ &\begin{cases} s_m \cos \varphi \left( {\left(RC\omega \right)}^2 + 1 \right) &= e_m\\ s_m \sin \varphi \left( {\left(RC\omega \right)}^2 + 1 \right) &= - RC \omega e_m \end{cases}\\ \Longrightarrow \\ &\begin{cases} s_m^2 \left( {\left(RC\omega \right)}^2 + 1 \right)^2 &= e_m^2\\ \tan \varphi &= RC \omega \end{cases}\\ \end{align*}\]

La résolution des dernières équations redonne bien les mêmes solutions.

Simplicité des complexes
En conclusion, l’intérêt de l’introduction des grandeurs complexes et bien sa grande simplicité (qui va être encore simplifiée par l’étude directe du circuit avec les grandeurs complexes). On détermine en effet une seule inconnue (la représentation complexe ou l’amplitude complexe) au lieu de deux (amplitude et phase à l’origine) en utilisant des systèmes d’équations linéaires et non des égalités de fonctions trigonométriques.

Impédances complexes

Nous avons vu comment, à partir de l’équation différentielle, obtenir un équation à une variable linéaire à résoudre simplement et comment de la représentation complexe ainsi déterminée remonter aux caractéristiques (phase à l’origine et amplitude) du régime sinusoïdal forcé.

Nous allons maintenant voir comment on peut “se passer” de l’établissement de l’équation différentielle en travaillant directement avec les grandeurs complexes. On obtiendra ainsi un système d’équations linéaire faisant intervenir les représentations complexes des grandeurs.

Pour ce faire, nous allons introduire la notion d’impédance.

Impédances complexes

Position du problème
Soit un dipôle linéaire passif. Dans un circuit en régime permanent sinusoïdal, il est parcouru par un courant \(i(t)=i_m \cos(\omega t + \phi_i)\) dont la représentation complexe est: \(\underline{i}(t)=i_m e^{j \phi_i} e^{j \omega t}\) et la tension à ses bornes est \(u(t) = u_m \cos(\omega t +\phi_u)\) dont la représentation complexe est: \(\underline{u}(t)=u_m e^{j \phi_u} e^{j \omega t}\).

Définition : Impédance complexe

On définit l’impédance complexe d’un dipôle par la grandeur:

(96)\[\begin{equation} \underline{Z} = \frac{\underline{u}}{\underline{i}} = \frac{\underline{u_m}}{\underline{i_m}} \end{equation}\]

Elle ne dépend pas du temps mais peut dépendre de la pulsation du circuit.

Important

Définition : Admittance complexe

On définit l’admittance complexe comme l’inverse de l’impédance complexe:

(97)\[\begin{equation} \underline{Y} = \frac{1}{\underline{Z}} = \frac{\underline{i}}{\underline{u}} = \frac{\underline{i_m}}{\underline{u_m}} \end{equation}\]

Ecriture complexe
On peut écrire: \(\underline{Z} = R + jX\) avec R et X réels. R est appelée la résistance du dipôle et X la réactance.

On peut écrire: \(\underline{Y} = G + jB\) où G et B sont des réels. G est appelé la conductance et B la susceptance.

On appelle impédance réelle \(Z\) le module de \(\underline{Z}\) et admittance réelle \(Y\) le module de \(\underline{Y}\).

Fondamental : Interprétation de l’impédance complexe

L’argument de l’impédance complexe définit le déphasage de la tension \(u\) par rapport à l’intensité \(i\).

Le module de l’impédance complexe est le rapport des amplitudes réelles des deux grandeurs.

Attention

On a \(\underline{Y} = \frac{1}{\underline{Z}}\) mais a priori \(R \neq \frac{1}{G}\) et \(X \neq\frac{1}{B}\)

Important

Fondamental : Intérêt des impédances

L’intérêt des impédances est qu’on peut traiter un circuit électrique en appliquant les lois de Kirchhoff directement avec les représentations complexes (car les lois de Kirchhoff sont linéaires) et en y introduisant des relations intensités-tension sous la forme \(\underline{u} = \underline{Z} \underline{i}\).

On pourra de même écrire: la loi des noeuds en terme de potentiels avec les représentations complexes des potentiels et les impédances(donc avec des condensateurs et bobines - cf. suite), les ponts diviseurs de tension et courant avec les impédances (donc avec des condensateurs et bobines dans les ponts) et on pourra associer des impédances comme on associe des résistances en série ou en parallèle.

Impédances des dipôles usuels

Important

Fondamental : Impédances usuelles

• Cas d’une résistance: \(\underline{Z} = R\)

• Cas d’une bobine: \(\underline{Z} = j L \omega\)

• Cas d’un condensateur: \(\underline{Z} = \frac{1}{jC \omega}\)

Démonstration
Le cas de la résistance est triviale.

Pour la bobine, l’équation d’évolution s’écrit: \(u = L \frac{\rm{d}i}{\rm{dt}}\) soit en complexe \(\underline{u} = j L \omega \underline{i}\)

Pour le condensateur, l’équation d’évolution s’écrit: \(i = C \frac{\rm{d}u}{\rm{dt}}\) soit en complexe \(\underline{i} = j C \omega \underline{u}\)

Remarque

On remarquera que l’impédance d’un condensateur est un imaginaire pur négatif. Les dipôles plus complexes qui possèderont une partie imaginaire négative seront dit à “effet capacitif”.

On remarquera que l’impédance d’une bobine est un imaginaire pur positif. Les dipôles plus complexes qui possèderont une partie imaginaire positive seront dit à “effet inductif”.

On remarquera que l’impédance d’une résistance est un réel pur positif. La partie réelle des dipôles plus complexes représentera les effets résistifs.

Méthode: Etude d’un circuit RLC série

Nous allons voir ici comment utiliser directement les représentations complexes sur un circuit.

Exercice

On considère un dipôle RLC série relié à une source idéale de tension délivrant une tension \(e(t) = e_m \cos \omega t\). Déterminer la tension aux bornes du condensateur et l’intensité traversant le dipôle en régime sinuoïdal forcé.

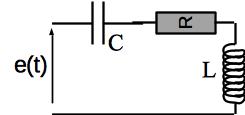
Correction

Méthode 1: Utilisation des lois de Kirchoff
La lois des mailles s’écrit: \(u_R + u_L + u_C = e\) et reste vraie avec les représentations complexes. En régime sinusoïdal forcé, on utilise les impédances: \(\underline{u_R} = R \underline{i}; \underline{u_L} = j L \omega \underline{i}; \underline{u_C} = \frac{\underline{i}}{jC \omega}\). Il vient:

(98)\[\begin{equation} \left(R + j L \omega + \frac{1}{j C \omega}\right) \underline{i} = \underline{e} \Longrightarrow \underline{i} = \frac{\underline{e}}{R + j L \omega + \frac{1}{j C \omega}} \end{equation}\]

On déduite la tension \(u_C\):

(99)\[\begin{equation} \underline{u_C} = \frac{\underline{i}}{jC \omega} = \frac{\underline{e}}{jRC \omega - LC \omega^2 + 1} \end{equation}\]

Méthode 2: Pont diviseur
R, L et C forment un pont diviseur de tension, il vient que:

\[\begin{align*} \underline{u_C} = \frac{\underline{Z_C}}{\underline{Z_R} + \underline{Z_L} + \underline{Z_C}} \underline{e} = \frac{\underline{e}}{jRC \omega - LC \omega^2 + 1}\\ \underline{i} = \frac{1}{\underline{Z_R} + \underline{Z_L} + \underline{Z_C}} \underline{e} = \frac{\underline{e}}{R + j L \omega + \frac{1}{j C \omega}} \end{align*}\]

Passage aux grandeurs réelles
On ne va travailler ici que sur l’intensité.

Amplitude réelle:

(100)\[\begin{equation} i_m = \left\vert \underline{i} \right\vert = \frac{e_m}{\sqrt{R^2 + {\left(L \omega - \frac{1}{C \omega}\right)}^2}} \end{equation}\]

Phase à l’origine:

(101)\[\begin{equation} \phi_i = \arg \underline{i} = \arg \underline{e} - \arg \left(R + j \left(L \omega - \frac{1}{C \omega}\right)\right) = - \arctan \frac{1}{R}\left(L \omega - \frac{1}{C \omega}\right) \end{equation}\]

Vérification du résultat.

En régime sinusoïdal forcé, on peut remarquer que \(C \omega\) est homogène à l’inverse d’une résistance et que \(L \omega\) est homogène à une résistance. Vous pouvez vérifier aisément que les grandeurs calculées sont homogènes (on rappelle qu’une phase est sans dimension).

D’autres vérification seront possibles lorsque nous aurons étudié les comportements asymptotiques.

Méthode: Etude d’un circuit.

Nous allons voir sur un exemple l’utilisation de la loi des noeuds en terme de potentiel.

Exercice

On considère le circuit ci-dessous où E est la tension d’entrée. Déterminer la tension \(\underline{s}\) aux bornes du condensateur en régime sinusoïdal forcé.

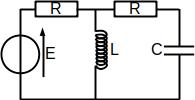
Correction

Paramétrage du problème.
On va utiliser la loi des noeuds en terme de potentiel donc on va nommer les potentiels et choisir une référence des potentiels. Remarquons qu’on sait que \(\underline{V_A} = \underline{E}\) et on cherche \(\underline{V_D} = \underline{u_C} + 0\).

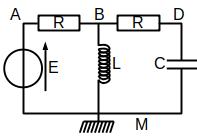
Application de la loi des noeuds en terme de potentiel
On va écrire deux lois des noeuds en termes de potentiel: en B et en D.

\[\begin{align*} &\begin{cases} \frac{\underline{V_B} - \underline{V_A}}{R} + \frac{\underline{V_B} - \underline{V_M}}{\underline{Z_L}} + \frac{\underline{V_B} - \underline{V_D}}{R} &= 0\\ \frac{\underline{V_D} - \underline{V_B}}{R} + \frac{\underline{V_D} - \underline{V_M}}{\underline{Z_C}} &= 0 \end{cases}\\ &\Longrightarrow \\ &\begin{cases} \frac{\underline{V_B} - E}{R} + \frac{\underline{V_B}}{j L \omega} + \frac{\underline{V_B} - \underline{V_D}}{R} &= 0\\ \frac{\underline{V_D} - \underline{V_B}}{R} + jC \omega \underline{V_D} &= 0 \end{cases}\\ &\Longrightarrow \\ &\begin{cases} \underline{V_B} = \left(1 + j RC \omega\right) \underline{V_D}\\ \left(2 + \frac{R}{jL\omega}\right)\underline{V_B} - \underline{V_D} = E \end{cases}\\ &\Longrightarrow \left(1 + j \left(2 RC\omega - \frac{R}{L\omega}\right) + \frac{R^2 C}{L}\right) \underline{V_D}= E\\ &\Longrightarrow \underline{s} = \underline{V_D} = \frac{E}{1 + j \left(2 RC\omega - \frac{R}{L\omega}\right) + \frac{R^2 C}{L}} \end{align*}\]

Vérification du résultat.

En régime sinusoïdal forcé, on peut remarquer que \(C \omega\) est homogène à l’inverse d’une résistance et que \(L \omega\) est homogène à une résistance. Vous pouvez vérifier aisément que les grandeurs calculées sont homogènes (on rappelle qu’une phase est sans dimension).

D’autres vérification seront possible lorsque nous aurons étudié les comportements asymptotiques.

Passage fréquentiel-temporel

Passage réel-complexe

On parle aussi de passer du temporel au fréquentiel et inversement.

Rappel : Passage du temporel au fréquentiel. On rappelle que si l’on a établit une équation différentielle reliant des grandeurs du système, on peut passer à la relation entre les grandeurs complexes correspondantes en remplaçant chaque dérivée temporelle par \(j\omega\).

Passage du fréquentiel au temporel

On peut aussi faire l’inverse et déduire d’une étude des grandeurs complexes, l’équation différentielle qui le relit. Il faut (pour deux grandeurs s et e reliée):

1. mettre le rapport \(\frac{\underline{s}}{\underline{e}}\) sous forme d’une fraction de deux polynômes en \(\omega\): \(\frac{P(j\omega)}{Q(j \omega)}\).

2. mettre l’égalité sous la forme\(Q(j \omega) \underline{s} = P(j \omega)\underline{e}\).

3. Remplacer chaque facteur \((j\omega)^n\) par la dérivée \(\frac{\rm{d^n}}{\rm{dt^n}}\)

Attention

Attention aux signes lorsqu’on passe du fréquentiel au temporel. En effet, le signe - pour le monôme de degré 2 vient en de \(j^2\) et doit disparaître (cf. exercice).

Méthode: Du fréquentiel au temporel

Exercice

On considère un système dont la relation entrée sortie entre les grandeurs complexes (on parle de fréquentiel) est:

(102)\[\begin{equation} \frac{\underline{s}}{\underline{e}} = \frac{1 - jRC \omega}{1 - LC \omega^2 + j RC \omega} \end{equation}\]

Déterminer l’équation différentielle qui relie les grandeurs \(s(t)\) à \(e(t)\).

Correction

On commence par exprimer l’équation sous forme \(P(j\omega) \underline{s} = Q(j \omega) \underline{e}\) où P et Q sous des polynômes en \(j \omega\):

(103)\[\begin{equation} \underline{s} - LC \omega^2 \underline{s} + j RC \omega \underline{s} = \underline{e} - jRC \omega \underline{e} \end{equation}\]

On remplacer chaque terme en \(j \omega\) par une dérivée temporelle:

(104)\[\begin{equation} s + LC \frac{\rm{d^2}s}{\rm{dt^2}} + RC \frac{\rm{d}s}{\rm{dt}} = e - RC \frac{\rm{d}e}{\rm{dt}} \end{equation}\]

Etude fréquentielle: Méthode et résultats importants

Exemple utilisé

Exercice Exemple de circuit utilisé

Dans toute la suite du chapitre, l’étude fréquentielle d’un circuit sera basée sur l’exemple du circuit RLC série. Il s’agit d’un exemple très classique qu’il faut maîtriser complètement.

On considèrera donc le circuit ci-dessous. On veut étudier le comportement fréquentiel de certaines grandeurs. On rappelle qu’il s’agit d’étudier les caractéristiques du régime sinusoïdal forcé pour une entrée sinusoïdale quelconque.

Etude haute et basse fréquence d’un circuit

Il est important de pouvoir analyser le comportement asymptotique d’un système, c’est-à-dire les comportements haute et basse fréquence. On peut pour celà utiliser deux méthodes:

• Etablir les équations et étudier le comportement limites des expressions complexes quand la pulsation tend vers 0 (basse fréquence) et vers l’infini (haute fréquence).

• Analyser directement le circuit en remplçant les condensateurs et bobines par des équivalents haute et basse fréquence. On parle d’étude rapide et l’on va préciser cette méthode.

Important

Fondamental : Comportements basse fréquence de C et L

A basse fréquence, un condensateur se comporte comme un interrupteur ouvert et une bobine comme un fil.

Démonstration
A haute fréquence, l’impédance du condensateur tend vers l’infini et celle de la bobine tend vers 0.

Important

Fondamental : Comportements haute fréquence de C et L

A haute fréquence, un condensateur se comporte comme un fil ouvert et une bobine comme un interrupteur.

Démonstration
A haute fréquence, l’impédance du condensateur tend vers 0 et celle de la bobine tend vers l’infini.

Remarque

Quantifier HF et BF.
En général dans les systèmes en physique, on arrive à exhiber une pulsation (et donc une fréquence) caractéristique appelée pulsation (fréquence) propre. Elle apparaît en général lorsqu’on veut mettre l’expression d’une grandeur sous une forme canonique (cf. suite).

On considère généralement qu’une haute fréquence est une fréquence grande devant la fréquence propre.

On considère généralement qu’une basse fréquence est une fréquence petite devant la fréquence propre.

Relecture

Les études hautes et basses fréquences sont utiles aussi pour la relecture. En effet, l’expression analytique d’une représentation complexe doit être cohérente avec ses comportements haute et basse fréquence. Si l’on trouve par une étude du circuit qu’une tension est nulle à haute fréquence, alors sa représentation complexe doit tendre vers 0 quand la pulsation tend vers l’infini par exemple. Il est conseillé (après avoir traité l’exemple donné ci-après) de reprendre les exemples traités précédemment et de faire l’analyse asymptotique du circuit. Vous vérifierez alors que les expressions trouvées sont cohérentes.

Méthode: Etude haute et basse fréquence

Exercice

Etudier la réponse haute et basse fréquence de l’intensité circulant dans le circuit et de la tension aux bornes du condensateur pour le circuit RLC série présenté précédemment.

Correction

Etude basse fréquence
A basse fréquence, le condensateur se comporte comme un interrupteur ouvert et la bobine comme un fil. Le circuit est donc assimilable au circuit suivant:

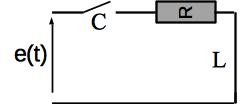
Il vient que l’intensité est nulle.

La loi des mailles s’écrit alors \(u_C = e - Ri = e\).

Etude haute fréquence
A haute fréquence, le condensateur se comporte comme un fil et la bobine comme un interrupteur ouvert. Le circuit est donc assimilable au circuit suivant:

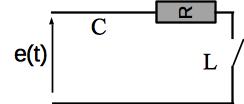
Il vient que l’intensité est nulle et la tension aux bornes du condensateur est nulle aussi (tension aux bornes d’un fil).

Intérêt
Nous allons voir que l’étude des comportements haute et basse fréquence permettent de prévoir le type de comportement fréquentiel ainsi que la forme canonique à donner à la représentation complexe de la grandeur étudiée.

Etude fréquentielle: Formes canoniques

L’expression des représentations complexes peuvent se mettre sous des formes de fractions de polynômes en \(j \omega\). On remarquera que la puissance maximale de ces polynômes correspond à l’ordre du système. Nous nous limiterons à des systèmes d’ordre 1 et 2.

On peut alors mettre la fraction sous une forme canonique faisant intervenir les caractéristiques du système: la pulsation propre et le facteur qualité pour un système d’ordre 2 par exemple.

Nous présenterons ici deux formes canoniques qui seront complétées par les formes canoniques des filtres dans le prochain chapitre.

Il faut pouvoir déterminer quelle forme est applicable à la grandeur étudié puis mettre l’expression calculée sous la forme en identifiant les élements caractéristiques (pulsation propre et facteur de qualité). Pour choisir la forme à appliquer, il faut connaître l’ordre du système et les comportements haute et basse fréquence.

Important

Fondamental : Comportement passe-bas d’ordre 2

Pour une grandeur d’un système d’ordre 2 dont le comportement haute fréquence est nul et le comportement basse fréquence non nul, sa représentation complexe peut se mettre sous la forme:

(105)\[\begin{equation} \underline{s} = \frac{A}{1 - {\left(\frac{\omega}{\omega_0}\right)}^2 + j \frac{\omega}{Q\omega_0}} = \frac{A}{1 - x^2 + j\frac{x}{Q}} \end{equation}\]

où \(x = \frac{\omega}{\omega_0} \) est appelée pulsation réduite (attention, elle est sans dimension!).

Important

Fondamental : Comportement passe-bande d’ordre 2

Pour une grandeur d’un système d’ordre 2 dont le comportement haute et basse fréquence est nul, sa représentation complexe peut se mettre sous la forme:

\[\begin{align*} \underline{s} &= \frac{A}{1 + j Q \left(\frac{\omega}{\omega_0} - \frac{\omega_0}{\omega}\right)} = \frac{A}{1 + jQ \left(x - \frac{1}{x}\right)}\\ &= \frac{A j\frac{\omega}{\omega_0 Q}}{1 - {\left(\frac{\omega}{\omega_0}\right)}^2 + j \frac{\omega}{\omega_0 Q}} = \frac{A j \frac{x}{Q}}{1 - x^2 + j \frac{x}{Q}} \end{align*}\]

où \(x = \frac{\omega}{\omega_0} \) est appelée pulsation réduite (attention, elle est sans dimension!).

Interprétation
Les termes passe-bas et passe-bande seront expliqué plus en détail au prochain chapitre mais on pourra déjà remarquer dans les études à venir qu’un passe-bas laisse passer les basses fréquences et qu’un passe-bande laisse passer une bande de fréquences.

previous

Régime sinusoïdal forcé

next

Activités d’application