Dipôles électriques: Généralités¶
Point de fonctionnement et caractéristique statique¶
Important
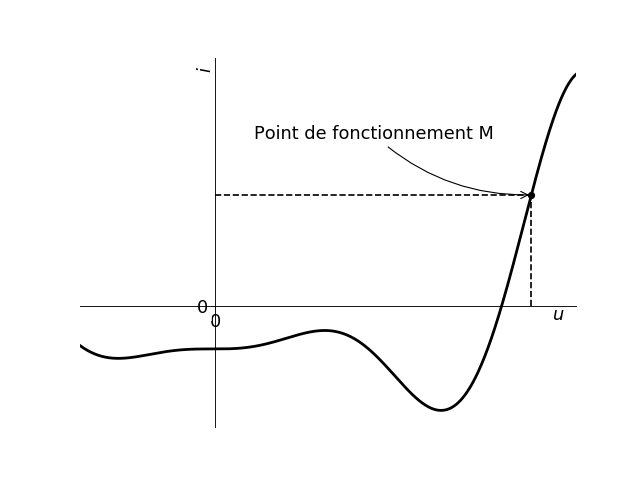
Définition : Point de fonctionnement
Un point de fonctionnement d’un dipôle est un couple \((U;I)\) de tension et intensité pouvant exister pour le dipôle en fonctionnement indépendant du temps.
Important
Définition : Caractéristique statique
La caractéristiques statique d’un dipôle est l’ensemble des points de fonctionnement du dipôle.
Attention
Caractère statique
Il s’agit d’un ensemble d’états statiques possibles regroupés sur le même graphique. Le système ne passe pas dynamiquement d’un point de fonctionnement à un autre puisque ces points sont établis dans un régime indépendant du temps.
Une caractéristique statique permet simplement de visualiser l’ensemble des états statiques possibles d’un dipôles.
Remarque
Dépendance vis-à-vis d’un paramètre
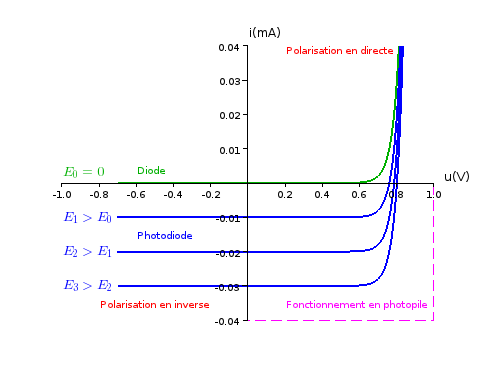
Fig. 8 Caractéristique statique d’une photodiode.¶
La caractéristique statique peut dépendre d’un paramètre extérieur.
Exemple: Une thermistance possède une caractéristique statique qui dépend de sa température et une photodiode possède une caractéristique qui dépend de l’éclairement (E). Souvent de tels dipôles sont utilisés comme capteur (de température pour le cas de la thermistance, de luminosité pour la photodiode… )
Typologie des dipôles¶
Important
Définition : Dipôle symétrique ou polarisé
Un dipôle symétrique est un dipôle dont la caractéristique statique est symétrique par rapport à l’origine (0;0).
En conséquence, un dipôle symétrique peut-être branché dans les deux sens sans changer son fonctionnement.
Un dipôle qui n’est pas symétrique est un dipôle polarisé
Le sens de branchement d’un dipôle polarisé a son importance.
Important
Définition : Dipôle passif ou actif
Un dipôle passif est un dipôle dont la caractéristique passe par l’origine.
Si la caractéristique ne passe pas par l’origine, on dit que le dipôle est actif.
Equation d’évolution¶
Important
Définition : Equation d’évolution
L’intensité qui traverse un dipôle est relié à la tension entre ses bornes par une équation mathématique appelée équation d’évolution du dipôle
Attention
Convention d’orientation
Souvent, les équations d’évolution sont données (ou à connaître) avec une certaine convention.
Exemple Equation d’évolution d’une diode
Pour une diode, l’équation d’évolution est en convention récepteur: \(i(u) = I_0 \left ( \exp ^{u/V_S} - 1\right )\)
Exemple Equation d’évolution d’une bobine
Pour une bobine, l’équation d’évolution est en convention récepteur: \(u(i) = L \frac{di}{dt}\)
Dipôle linéaire¶
Important
Définition : Dipôle linéaire
Un dipôle est dit linéaire si son équation d’évolution est une équation différentielle linéaire.
L’ordre de l’équation différentielle est le rang de la dérivée la plus grande.
Circuit linéaire
Un circuit linéaire est un circuit composé uniquement de composants linéaires.
Caractéristique statique des dipôles linéaires¶
Important
Fondamental : Caractéristique statique des dipôles linéaires
La caractéristique statique d’un dipôle linéaire est une droite dont l’équation s’écrit \(a_0 U - b_0 I = F_0\).
Démonstration
Pour déterminer la caractéristique statique, il faut éliminer toute variation temporelle de l’équation d’évolution. Dans l’équation d’évolution d’évolution d’un dipôle linéaire, cela revient à annuler toutes les dérivées temporelles (il ne reste que \(a_0 u(t)\) et \(b_0 i(t)\)) et ne garder que le terme constant de F(t).
Remarque
Dipôles linéaires passifs et actifs
Si \(F_0 = 0\) le dipôle est passif. Il est alors aussi symétrique.
Si \(F_0 \neq 0\) il est actif (on parle de source).
Attention
Caractéristique statique et évolution temporelle
Seule la caractéristique statique est une droite. On rappelle qu’il s’agit du regroupement de l’ensemble des états possibles dans des cicuits en régime indépendant du temps.
On peut aussi tracer l’évolution (u(t);i(t)) (on parle de caractéristique dynamique) pour un dipôle dans un circuit donné. Il ne s’agit alors pas nécessairement d’une droite.