.ipynb .md .pdf

Binder

Contents

Association de résistances

Dipôle équivalent

Définition : Dipôle équivalent

Deux dipôles sont équivalents s’ils ont la même équation d’évolution

Méthode : Démontrer une équivalence

Comme l’indique la définition, la méthode principale pour démontrer ou déterminer une équivalence est de déterminer l’équation d’évolution des deux dipôles et de procéder à une identification des termes.

Nous verrons aussi des cas d’équivalence à connaître qui peuvent être utilisés directement.

Résistances en série

Important

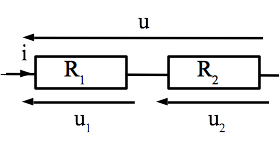
Fondamental : Résistance équivalente à deux résistances en série Deux résistances $R_1$ et $R_2$ en série sont équivalentes à une seule résistance de valeur $R_{eq} = R_1 + R_2$

Démonstration
Comme expliqué précédemment, il suffit d’exprimer l’équation d’évolution. Ici, les deux résistances étant en série, la tension aux bornes de l’ensemble est la somme des tensions aux bornes de chaque dipôle: $u = u_1 + u_2 = R_1 i + R_2 i = (R_1 + R_2) i$

L’équation d’évolution d’une résistance étant $u = R_{eq} i$, on peut identifier les deux expressions avec $R_{eq} = R_1 + R_2$.

Complément : Généralisation

N résistances de valeurs $\{R_i \vert i \in [\![1;n]\!]\}$ en série sont équivalentes à une seule résistance de valeurs $R_{eq} = \sum_{i=1}^{i=n} R_i$

Résistances en parallèle

Important

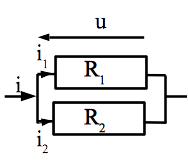
Fondamental : Résistance équivalente à deux résistances en parallèle

Deux résistances $R_1$ et $R_2$ en parallèle sont équivalentes à une seule résistance de valeur $R_{eq} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2}}$ (soit de conduction $G_{eq} = G_1 + G_2$)

Démonstration
Comme expliqué précédemment, il suffit d’exprimer l’équation d’évolution. Ici, les deux résistances étant en parallèle, l’intensité qui entre dans le dipôle complet est la somme des intensités circulant dans chaque dipôle: $i = i_1 + i_2 = \frac{u}{R_1} + \frac{u}{R_2} = u (\frac{1}{R_1} + \frac{u}{R_2}) i$

L’équation d’évolution d’une résistance étant $i = u\frac{1}{R_{eq}}$, on peut identifier les deux expressions avec $\frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2}$.

Complément : Généralisation

N résistances dont les conductances sont $\{G_i \vert i \in [\![1;n]\!]\}$ en parallèle sont équivalentes à une seule résistance dont la conductance est $G_{eq} = \sum_{i=1}^{i=n} G_i$

Méthode: Dipôle équivalent par les équations d’évolution

On se propose ici de voir comment déterminer un dipôle équivalent plus simple (une résistance ) à partir d’un maillage. On verra aussi l’utilisation des symétries.

Exercice

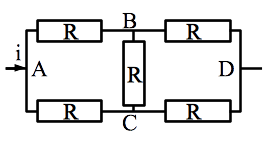
Déterminer la résistance équivalente au réseau de résistance ci-contre.

Exemple d’application

On va déterminer la relation tension-intensité. Mais pour simplifier le problème, remarquons que le maillage est symétrique par rapport à l’axe du fil. Cela implique que toutes le grandeurs sont symétrique. Ainsi, le potentiel au point B et au point C sont égaux et les intensités circulant dans les branches AB et AC (ou BD et CD) sont égales.

La loi des noeuds en A et D implique immédiatement que $i_{AB} = i_{AC} = i/2 = i_{BD} = i_{CD} = i/2$ (on a orienté les intensités en cohérence avec l’ordre des indices).

On peut maintenant calculer la tension entre A et D en fonction de i en passant par un chemin (par exemple le chemin ABD):

$u_{AD} = u_{AB} + u_{BD} = R i/2 + R i/2 = R i$

Par identification ($u = R_{eq} =i$), il vient que la résistance équivalente au maillage est R.

Méthode: Dipôle équivalent par manipulation des schémas

On se propose ici de voir comment déterminer un dipôle équivalent plus simple (une résistance ) à partir d’un maillage. Nous utilisons cette fois des transformations successives des circuits basés sur les résistances équivalentes établies précédemment.

Exercice

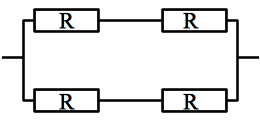
Déterminer la résistance équivalente au réseau de résistance ci-contre.

Exemple d’application

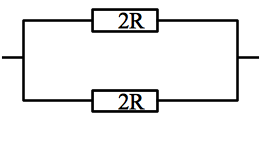
On remarque que dans chaque branche, les deux résistances R sont en série, donc équivalente à une résistance 2R.

On remarque que dans chaque branche, les deux résistances 2R sont en parallèle, donc équivalente à une résistance $R_{eq} = \frac{1}{\frac{1}{2R}+\frac{1}{2R}} = R.$

Donc le dipôle est équivalent à une seule résistance de valeur R.

Dipôles linéaires passifs Dipôles linéaires actifs