Dipôles linéaires actifs¶
Sources idéales¶
Important
Définition : Source idéale de tension
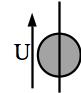
Fig. 12 Schéma d’une source idéale de tension¶
Une source idéale de tension est un dipôle dont la tension est une caractéristique propre du dipôle et ne varie pas, quelque soit l’intensité qui la traverse.
On appelle la tension à ses bornes force électromotrive (f.e.m.)
Important
Définition : Source idéale de courant
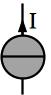
Fig. 13 Schéma d’une source idéale de courant¶
Une source idéale de courant est un dipôle dont l’intensité est une caractéristique propre du dipôle et ne varie pas, quelque soit la tensionà ses bornes.
On appelle l’intensité qui la traverse courant électromoteur (c.e.m.)
Attention
Source: dipôle polarisé
Les sources sont des dipôles polarisés. Il est important de préciser le sens dans lequel est orienté la f.e.m. ou le c.e.m.
Caractéristique statique
La caractéristique statique d’une source idéale de tension de fem E est une droite verticale d’équation u = E
La caractéristique statique d’une source idéale de courant de cem I est une droite horizontale d’équation i = I
Source réelle: Electromoteur¶
Comportement réels des sources
En pratique, une source de tension ne délivre la fem voulue E qu’à vide, c’est-à-dire quand aucun courant ne sort.
Lorsqu’on commence à demander une intensité en sortie (donc de la puissance), la fem u tend à diminuer.
Expérimentalement, on observe qu’on peut modéliser cette chute par un modèle linéaire: u = E - Ri. C’est le modèle des électromoteurs.
Important
Définition : Electromoteur
Un électromoteur linéaire est une modélisation d’une source donc la relation tension-intensité est:
\(u = E - Ri\) ou \(i = \eta - G u\)
E est la fem (à vide) de l’électromoteur et R sa résistance interne.
\(\eta\) est le cem (à vide) de l’électromoteur et G sa conductance interne.
Lien entre les grandeurs
On peut passer d’une équation à l’autre puisque les grandeurs \(E, \eta, R\) et G peuvent être reliées entre elles.
Important
Fondamental : Modélisation de Thévenin d’un électromoteur
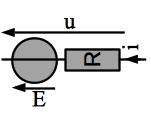
Un électromoteur peut être modélisé par une source idéale de tension de fem E en série avec une résistance R
Démonstration
Comme à chaque fois pour prouver/déterminer l’équivalence de deux dipôles, nous allons exprimer la relation intensité tension. Dans le cas de l’électromoteur, on a déjà \(u = E - Ri\)
La tension aux bornes du modèle proposé est (la résistance est orientée en convention générateur): \(u = E + u_R = E - R i\)
On a bien identification des équations d’évolution, donc l’électromoteur est modélisable par le modèle de Thévenin.
Attention
C’est une modélisation
Le modèle est Thévenin est comme son nom l’indique une modélisation, c’est-à-dire qu’elle permet d’étudier mathématiquement le comportement de la source réelle mais ne traduit pas la composition physique de la source (qui est bien plus complexe).
Méthode: Déterminer un modèle de Thévenin équivalent¶
Cet exercice propose d’apprendre à montrer qu’un dispositif peut être remplacé par un modèle de Thévenin en déterminant ses caractéristiques. Nous étudierons deux méthodes: l’établissement de l’équation d’évolution comme utilisé précédemment pour la détermination d’un dipôle équivalent et le calcul de deux points particuliers.
Exercice
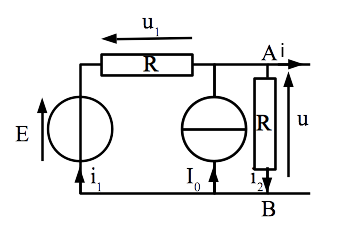
Montrer que le circuit ci-dessous est équivalent à un modèle de Thévenin entre les bornes A et B dont on déterminera les caractéristiques.
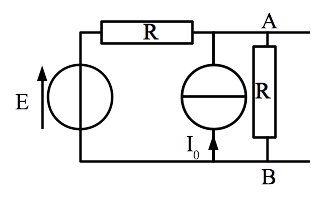
Correction
On commence par paramétrer le circuit et à bien réfléchir aux grandeurs:
qu’on doit chercher. Ici on veut exprimer la relation tension-intensité. On va donc chercher u en fonction de i ou i en fonction de u. Pour des raisons totalement arbitraires, on décide chercher u en fonction de i.
qu’on connaît: la fem E, le cem \(I_0\), la valeur de résistance R. L’intensité i devient aussi une grandeur qu’on “connait” puisqu’on veut exprimer u en fonction de i.
les grandeurs qui restent doivent être éliminées (il n’est même pas utile de les déterminer en fonction des données du problème puisqu’elle ne sont pas utiles à l’étude demandée). En général, ce sont des grandeurs que nous avons introduites, ici \(i_1, u_1, i_2\)
On a donc 4 inconnnues (\(u, i_1, u_1, i_2\)). Il faudra donc quatre équations.
Remarque
Orientation des grandeurs
On a orienté i et u en convention générateur de manière à pouvoir identifier la relation u(i) à la relation attendue du modèle de Thévenin en convention générateur \(u = E_{Th} - R_{Th} i\)
On a orienté \(i_2\) de cette façon pour que la résistance soit en convention récepteur. Le but est de pouvoir utiliser directement la loi d’Ohm (écrite en convention récepteur) sans se tromper dans les signes. Encore une fois, le choix de la convention étant arbitraire, on aurait pu choisir une convention générateur. Il est judicieux de choisir une convention récepteur, non pas pour des raisons physiques, mais pour ne pas se tromper dans les formules…
On réalise la mise en équation (nous utilisons ici les lois des mailles et des noeuds mais il est vivement conseillé de s’entraîner à cet exercice en appliquant la loi des noeuds en terme de potentiel):
Avec les deux lois d’Ohm \(u_1 = R i_1\) et \(u = R i_2\) on dispose de 4 équations donc d’autant d’équations que inconnues.
Remarque : Sur la loi des noeuds
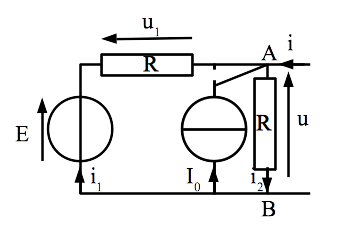
La loi des noeuds peut sembler à certains étranges puisque les intensités ne semble pas courir en un noeud. Néanmoins, on rappelle que sur un fil de connexion, le potentiel est identique partout et le point de raccordement du noeud importe alors peu. On a reproduit ci-contre le schéma équivalent au précédent permettant de faire apparaître le noeud où l’on applique la loi de Kirchhoff.
La règle principale est d’éliminer les grandeurs qui ne nous intéresse pas ET DE GARDER JUSQU’AU BOUT LA GRANDEUR QU’ON VEUT CALCULER.. Ici, on va éliminer \(u_1\) et \(i_2\) en utilisant les lois d’Ohm. Il vient :
En multipliant par R la première équation et en sommant, il vient:
Par identification, on trouve:
Correction - Autre méthode
On propose d’utiliser une autre méthode pour déterminer les caractéristiques du modèle de Thévenin équivalent. Le principe est basé sur le fait qu’une caractéristique statique d’un dipôle linéaire est une droite. Il suffit donc de connaître deux points de la droite pour connaître ses caractéristiques.
On va choisir deux points simples à étudier:
Le cas où l’on impose i = 0 (on parle de coupe-circuit). On cherche u.
Le cas où l’on impose u = 0 (on parle de court-circuit). On cherche i.
Cas i = 0
La loi des noeuds s’écrit \(i_1 + i_0 = i_2 = \frac{u}{R}\)
La loi des mailles s’écrit: \(E - R i_1 = u\)
Une combinaison linéaire pour éliminer \(i_1\) donne \(E + R i_0 = 2 u\)
Cas u = 0
La loi des noeuds s’écrit \(i_1 + i_0 = i + i_2 = i\)
La loi des mailles s’écrit: \(E - R i_1 = u = 0\)
Une combinaison linéaire pour éliminer \(i_1\) donne \(E + R i_0 = R i\)
La droite du modèle de Thévenin doit donc passer par les points \((0;\frac{E}{R} + i_0)\) et \((\frac{E + R i_0}{2}; 0)\)
On cherche une droite de la forme \(u = E_{Th} - R_{Th} i\) passe par les deux point précédents (attention les coordonnées sont (u ; i)).
Une recherche mathématique classique du coefficient directeur donne \(R_{Th} = R / 2\).
La valeur de la fem est directement donnée au point i=0.