Décrire la conduction électrique à notre échelle : Courant et Tension¶
Charge électrique¶
Important
Définition : Charge électrique
La charge électrique est une propriété fondamentale de la matière qui lui permet d’interagir avec les champs électromagnétiques.
L’unité usuelle de mesure de la charge électrique est le Coulomb (C).
Important
Fondamental : Conservation de la charge
La charge est une grandeur qui se conserve, c’est-à-dire qu’elle ne peut ni être détruire, ni être produite.
Important
Fondamental : Quantification de la charge
On observe1 que la charge Q de tout système est un multiple entier de la charge élementaire \(e = 1.609 \times 10^{-19} \rm{C}\).
Exercice Exemple de particules chargées
Les particules chargées sont:
les électrons (de charge -e)
les protons (charge e) et noyaux
les ions (cations et anions)
Conduction et courant¶
Phénomène de conduction¶
Conduction
Le phénomène de conduction correspond au déplacement de charges dans un matériau (solide ou liquide).
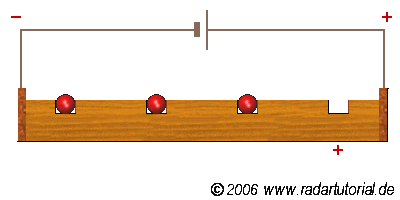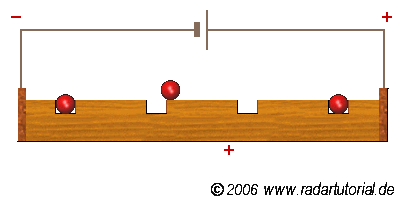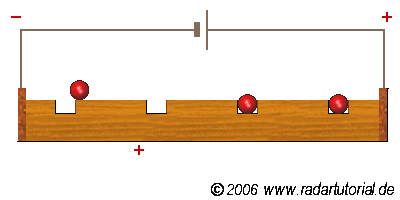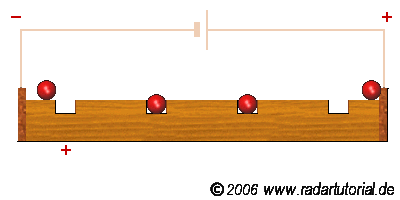
Fig. 1 Conduction par lacune électronique¶
Les charges de conduction peuvent être de natures diverses.
des électrons
des ions
des lacunes électroniques, c’est-à-dire le déplacement de proche en proche d’un manque d’électrons.
Important
Définition : Courant électrique et intensité.
Le courant électrique à travers une section S orienté arbitrairement correspond au passage des charges de conduction à travers cette section par unité de temps.
La grandeur mesurant le courant électrique est l’intensité du courant. Elle se définit comme le débit de charge à travers la surface, c’est-à-dire la quantité de charge traversant la surface S par unité de temps.
Attention
Caractère algébrique de la charge
Pour chaque charge q traversant la section S, la charge q est ajoutée au bilan de quantité de charges si elle se déplace dans le sens d’orientation de la surface S et est enlevée au bilan si elle se déplace dans l’autre sens.
Mais les charges sont algébriques : elles peuvent être positives ou négatives. Donc si une charge négative traverse la surface dans le “bon sens” c’est-à-dire dans le sens d’orientation de S, elle va diminuer la valeur de l’intensité et non l’augmenter.
Si l’on considère sur le schéma que toutes les charges représentées vont traverser la surface S durant 1 seconde, alors la charge \(\Delta Q\) qui va traverser S est :
\(Q_{Tot} = Q_1 + Q_2 + Q_3 - Q_4 - Q_5 - Q_6\)
\( = -3 + 0.25 + 1.5 - 2.5 - (-0.25) - 2 = - 5.5 C\)
d’où une intensité \(i = \frac{Q_{Tot}}{\Delta t} = - 5.5 A\).
Remarque : Cette valeur est très grandeur et les charges des porteurs de charge sont en réalité beaucoup plus faibles.
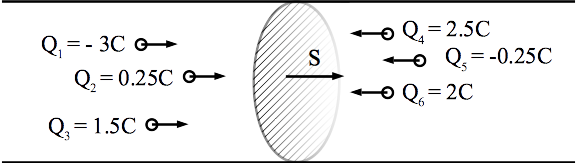
Fig. 2 Caractère algébrique des charges¶
Remarque
Orientation de l’intensité
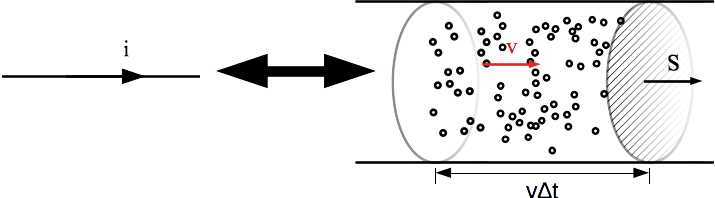
Fig. 3 Représentation de l’intensité dans un circuit normalisé¶
L’orientation de la surface correspond dans les schémas électriques habituels à l’orientation de l’intensité. Cette orientation est arbitraire.
Dans ces représentations, on ne tient pas compte de l’épaisseur du fil.
Attention
Caractère algébrique
L’orientation de l’intensité dans un fil est arbitraire. C’est la personne qui fait l’étude (ou qui pose la question… ) qui choisit l’orientation. Il n’est pas nécessaire qu’elle correspondent au phénomène réel de conduction. Il n’y a donc pas à réfléchir physiquement à ce qui se passe dans le circuit pour orienter i.
Trouver une intensité négative n’est PAS une erreur. Cela veut simplement dire que le débit de charge est positivement dans l’autre sens.
Remarque : Comme dans la plupart des études que nous ferons la conduction sera assurée par des électrons, le débit des porteurs de charge sera en général inverse en sens d’une intensité positive.
Intensité et intensité moyenne¶
Intensité moyenne
L’intensité moyenne consiste à mesurer le débit de charge pendant un temps \(\Delta t\) fini. On divise alors la quantité de charge (algébrique) par la durée pour obtenir l’intensité moyenne.
Intensité
L’intensité qu’on calcule générale est l’intensité instantanée, c’est-à-dire la mesure du débit en faisant tendre la durée \(\Delta t\) vers 0. En utilisant les notations différentielles, on a alors :
avec q la quantité de charge traversant la surface orientée.
Méthode : Calculer une intensité par des considérations microscopiques.¶
Cette méthode ne sera pas souvent utilisée dans ces chapitres mais est très utile pour comprendre le passage du microscopique au macroscopique.
Exercice
Estimer le nombre d’électrons par unité de volume pouvant participer à la conduction électrique. On donne :
Masse molaire du cuivre : \(M_{Cu} = 63.5 \rm{g.mol^{-1}}\)
Masse volumique du cuivre : \(\rho_{Cu} = 9 \times 10^3 \rm{kg.m^{-3}}\)
Correction
Les atomes de cuivre qui composent le métal ne perdent en général qu’un ou deux électrons pour former des ions. On peut donc considérer qu’il y a pour un atome de cuivre, un électron de conduction. La densité d’électron de conduction est donc du même ordre de grandeur que la densité d’atomes de cuivre.
\(n_{e} = n_{Cu} = N_A \frac{\rho_{Cu}}{M_{Cu}} = 6 \times 10^{23} \times \frac{9 \times 10^3}{63.5 \times 10^{-3}} = 10^{29} \rm{electrons.m^{-3}}\)
Exercice
On considère un fil de cuivre de section \(S = 1 \rm{mm^2}\) parcourue par une intensité \(I = 1 \rm{A}\). Estimer la vitesse des électrons en considérant qu’ils ont tous la même vitesse. Commenter cette vitesse.
Correction
Comptons combien d’électrons traversent une section \(S\) durant un temps \(\Delta t\)
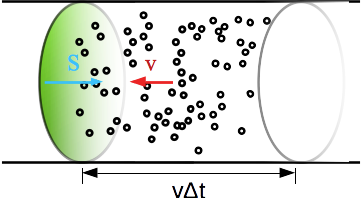
Fig. 4 Quantité de charge¶
Considérons l’instant initial \(t\) et cherchons quelles sont les caractéristiques d’un électron qui va traverser la surface S entre t et \(t + \Delta t\). Il doit (avec les conventions de vitesse choisis sur le schéma - inverser la vitesse des électrons ne changerait pas la valeur de i en valeur absolue, cela ne ferait que changer le signe) :
être à droite (sur le schéma) de la section S
être à une distance inférieure à \(v \Delta t\) de la section S car la distance qu’il va parcourir est \(v \Delta t\)
Si ces deux conditions sont réunis, l’électron va immanquablement traverser la section S donc tous les électrons qui se trouvent dans le cylindre de base S et de hauteur \(v \Delta t\) à l’instant t traverseront la section S entre t et \(t + \Delta t\).
Utilisons la question précédente, la quantité d’électrons est : \(N_{e-} = -n_{e} S v \Delta t\) (le signe - vient du fait que les électrons se déplacent dans le sens inverse de l’orientation de la section) donc l’intensité est :
\(i = \frac{\Delta q}{\Delta t} = \frac{- (-e) n_{e} S v \Delta t}{\Delta t} = n_e e S v\)
Il vient une vitesse :
\(v = \frac{i}{n_e e S} = \frac{1}{\times 10^{29} \times 1.6 \times 10^{-19} \times 10^{-6}} = 6 \times 10^{-5} m.s^{-1}\)
Remarque
On remarque que la vitesse est très faible, surtout comparée aux vitesses d’agitation thermique qui sont de l’ordre de plusieurs centaines de mètre par seconde. La conduction thermique correspond donc plutôt à une lente dérive des électrons tandis qu’ils s’agitent dans tous les sens.
Ordres de grandeur des courants électriques¶
Voici l’ordre de grandeur de intensités qu’on peut rencontrer :
Circuits étudiés en TP de physique : quelques mA au maximum.
Courant pouvant provoquer une paralysie : 10mA
Limite officielle de fuite de courant : 30mA
Ampoule à incandescence : 1A
Radiateur électrique: 10A
Eclair : 10-100kA
Potentiel électrique et tension¶
Sans excitation extérieur, ils n’y a pas de mouvement d’ensemble des charges, c’est-à-dire de conduction électrique. Pour ce faire, il faut mettre les charges en mouvement. Comme toujours en mécanique, la mise en mouvement nécessite une force. Ici c’est le champ électrique (créé directement ou indirectement par la source : un générateur ou une pile) qui exerce une force sur les charges de conduction.
Potentiel électrique¶
Action d’un champ électrique sur une particule chargée
Lorsqu’un champ électrique2 \(\overrightarrow{E}\) est établi dans un milieu, les charges \(q\) du milieu subissent une force \(\overrightarrow{F} = q \overrightarrow{E}\).
Important
Définition : Potentiel électrique
La force qu’exerce un champ électrique sur une charge \(q\) dérive d’une énergie potentielle. Si l’on note \(E_{p,el}\) l’énergie potentielle associée à cette force sur une charge q en un point A du circuit, on définit le potentiel électrique \(V_A\) du circuit au point A par \(V_A = \frac{E_{p,el}}{q}\).
Indépendance vis-à-vis des charges de conduction.
Le potentiel électrique dépend du point du circuit considéré et évidemment des composants du circuit. Mais il ne dépend pas de la charge qui assure la conduction. Ainsi, on peut parler du potentiel électrique d’un point du circuit et non de la charge.
Ce point est important car il permet de commencer à étudier un circuit grâce à deux paramètres accessibles à notre échelle (l’échelle macroscopique) sans se préoccuper des phénomènes microscopiques et de leur complexité :
l’intensité du courant en chaque point du circuit.
le potentiel électrique de chaque point du circuit.
Comme nous le verrons par la suite, nous pourrons encore diminuer le nombre de paramètres nécessaires.
Important
Définition : Référence des potentiels - Masse
Comme l’énergie potentielle, le potentiel est défini à une constante près. On peut donc choisir le point du circuit où le potentiel électrique est nul. On parle de référence des potentiels ou masse.
Fig. 5 Symbole d’un point de masse dans le schéma d’un circuit électrique¶
Important
Définition : Tension (différence de potentiel)
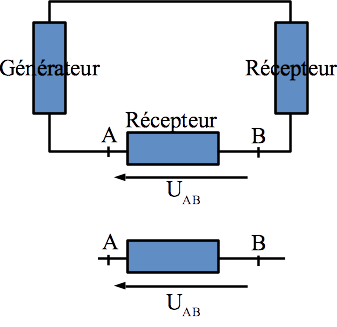
Fig. 6 Représentation d’une tension sur un circuit¶
On appelle tension \(U_{AB}\) (ou différence de potentiel entre deux points A et B) la différence \(U_{AB} = V_A - V_B\).
Dans un schéma de circuit électrique, elle est représentée par une fléche pointant vers le premier point (ici A).
Interprétation de la tension.
Pour une charge \(q\) passant d’un point A à un point B sa variation d’énergie potentielle est \(\Delta E_p = q (V_B - V_A) = - q U_{AB}\) : il s’agit de l’énergie perdue (ou gagnée suivant les signes de q et \(U_{AB}\)) au passage dans un composant. Ce point de vue est important pour la suite car il permettra de décrire les échanges énergétiques entre un composant (on parlera de dipôle) et le reste du circuit.
Remarque
Additivité des tensions.
Considérons trois points du circuit A,B et C. On peut utiliser l’additivité des tensions : \(U_{AC} = U_{AB} + U_{BC}\) en effet \(U_{AC} = V_A - V_C = V_A - V_B + V_B - V_C\)
Analogie entre un circuit hydraulique et un circuit électrique¶
Pour comprendre le principe général d’un circuit électrique et le rôle de l’intensité et du potentiel électrique, on peut faire l’analogie entre un circuit d’eau entièrement fermé et un circuit électrique.
L’analogie est présentée sous forme d’exercices mais les méthodes utilisées ne sont pas à connaître. Il s’agit surtout de comprendre le fonctionnement physique d’un circuit électrique.
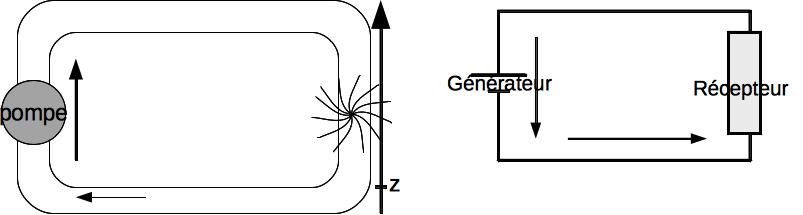
Fig. 7 Analogie circuit hydraulique et circuit électrique¶
Grandeurs analogue ?
Questions :
Comment appelle-t-on la grandeur qui caractérise le déplacement d’eau dans la conduite ?
Dans un circuit hydraulique, quelle énergie est gagnée/perdue par les petits “blocs” d’eau lorsqu’ils se déplacent dans le circuit ?
Réponses :
Dans le circuit hydraulique, c’est le débit massique d’eau qui est analogue à l’intensité électrique.
Dans le circuit hydraulique, les “blocs” d’eau (on parlera de particules de fluide) gagnent ou perdent de l’énergie potentielle de pesanteur. Elle est analogue à l’énergie potentielle électrique des charges. On pourra associer à cette énergie potentielle un potentiel de pesanteur (\(E_{p,pes} / m = g z\)) qui ne dépend que de la Terre (du champ de pesanteur terrestre) et de la position dans le circuit et pas de la masse d’eau considérée. Elle est analogue au potentiel électrique.
Échanges énergétiques
Questions :
Quel est le rôle de la pompe ?
En circuit fermé et en régime stationnaire, comment évolue le débit d’eau le long du circuit ?
En déduire un bilan d’énergie pour l’eau avant et après la turbine (composant à droite). Faire l’analogie avec la traversée du récepteur.
Réponses :
La pompe prend de l’eau à faible hauteur pour l’amener à une hauteur importante : elle donne de l’énergie aux “blocs” d’eau mais ne crée pas de l’eau. De même un générateur ne crée pas des charges,__ il leur donne de l’énergie__. Attention quand même, les électrons libérées au pôle (-) ne sont pas les mêmes que les électrons absorbées au pôle (+) (On pourra penser à une pile électrochimique). Le bilan se fait sur l’ensemble des électrons de conduction du circuit, pas sur un électron pris tout seul (un peu comme un circuit hydraulique où la pompe prélèverait et rendrait l’eau à une rivière).
Le débit d’eau ne peut varier car l’eau est incompressible. Un volume qui avance dans la conduite pousse le volume qui le précède qui avance de la même manière : dans toutes les sections de la conduite, le débit étant le même, l’énergie cinétique ne varie pas le long du circuit. Il en est de même pour les charges électrique en régime stationnaire : l’intensité du courant est la même tout au long du circuit. Attention, cela suppose un circuit à une voie, il ne doit pas y avoir de bifurcation.
En passant dans la turbine, l’eau garde la même énergie cinétique mais perd de l’énergie potentielle : elle perd donc de l’énergie. Cette énergie est apportée à la turbine pour la faire tourner : la turbine reçoit de l’énergie (qu’elle transforme en une autre forme d’énergie, ici de l’énergie cinétique). Si l’échange se fait avec le fluide du circuit, on peut faire abstraction du fluide et considérer qu’il y a un échange d’énergie entre la pompe et la turbine. Il en est de même dans un circuit électrique. Les électrons, au passage dans le récepteur perdent de l’énergie (puisque leur énergie potentielle \(-eV\) diminue - V augmente - et que leur énergie cinétique reste identique), cette énergie est reçue par le récepteur. On peut considérer que les électrons de conduction servent de transfert : le générateur fournit de l’énergie qui est reçue par le récepteur.
Ordre de grandeurs des tensions¶
Voici quelques ordres de grandeur des tensions qu’on peut rencontrer :
En TP : De quelques mV à plusieurs V
Piles : Entre 1.5 et 9V et Batteries : 6 à 24V (tension indépendante du temps)
Réseau de distribution EDF : Valeur efficace : 220V (tension sinusoïdale)
Ligne haute tension : 150 à 500 kV
Foudre : 100000 à 500000 kV
Approximation des régimes quasi-stationnaires¶
Nous avons vu que la description d’un circuit électrique passe par un nombre restreint de paramètres :
l’intensité circulant dans les branches (nous préciserons ce point dans le paragraphe)
le potentiel électrique aux différents points du circuit (ou les tensions entre les différents points du circuits)
Nous étudierons des régimes indépendants du temps, c’est-à-dire dans lequel toutes les grandeurs (tensions et intensités) ne dépendant pas du temps. Néanmoins, souvent, des perturbations dans le circuit (allumage/extinction du générateur par exemple) pourront survenir et les grandeurs vont pouvoir varier dans le temps. \end{intro}
Ondes électriques dans les circuits¶
Propagation des perturbations dans un circuit. Célérité.
Lorsqu’on perturbe un point du circuit (en modifiant par exemple le potentiel électrique ou l’intensité en un point du circuit), cette perturbation se transmet le long du circuit. On peut parler d’onde électrique.
La célérité des ondes électriques dans un circuit est de l’ordre de la célérité de la lumière \(c = 3 \times 10^8 m.s^{-1}\).
Exercice Temps de propagation
Question : Dans un circuit de TP, quel temps une perturbation met pour se propager à l’ensemble du circuit.
Réponse : Les circuits de TP ont une taille de l’ordre de 1m, donc la durée de propagation est \(1/(3\times 10^{8}) = 3 \times 10^{-9} s\).
Exercice Différence entre célérité de l’onde et déplacement des électrons
Il faut bien faire la différence entre la célérité de l’onde (\(3 \times 10^8 m.s^{-1}\)) qui correspond à la vitesse de transmission d’une information le long d’un circuit et la vitesse de dérive des électrons (moins d’un mm par seconde) dans le circuit.
On peut faire l’analogie suivante : on lâche un petit morceau de bois dans une rivière qui s’écoule doucement. Le bois va flotter et être emporté à la même vitesse que la rivière. Au moment d’entrée dans l’eau, le bois crée des remous qui vont se propager : il naît une onde à la surface de l’eau.
La célérité de l’onde à la surface (qui transporte l’information : “le bois est entré dans l’eau et a mis en mouvement la surface” comme l’onde électrique propagée de proche en proche dans le fil transporte l’information de la perturbation initiale) est en général beaucoup plus rapide que la vitesse de l’eau dans la rivière (qu’on peut matérialiser par le mouvement du bois et qui correspond au mouvement des électrons dans l’eau).
Au passage, cette analogie peut continuer si l’on observe que le mouvement de l’eau se décompose en deux parties : le mouvement de dérive qui correspond à l’écoulement global de la rivière et un mouvement chaotique des petites molécules d’eau dans la rivière. Le premier est visible à l’oeil nu comme l’intensité électrique est mesurable (grâce à un ampèremètre) alors que le second est invisible à notre échelle (comme l’est l’agitation des électrons)
Approximation des régimes quasi-stationnaires (ARQS)¶
Important
Définition : Approximation des régimes quasi-stationnaires (ARQS)
Un circuit dans lequel le temps de propagation des perturbations est très faible devant le temps de variation des grandeurs en un point du circuit est un circuit fonctionnant dans l’approximation des régimes quasi-stationnaires.
On peut alors considérer que les phénomènes de propagation sont instantanés et que les grandeurs du circuits (potentiel et intensités) varient en même temps sous l’effet d’une perturbation.
Attention : le fait qu’elles varient en même temps ne signifie pas qu’elles varient de la même manière.
C’est bien la variation spatiale associée à la propagation de l’onde électrique qui est négligée, pas la variation temporelle des grandeurs : en un point (et donc en tout point) du circuit, tension et intensité peuvent varier.
Exercice Analogie avec la voix
Pour comprendre le principe de l’ARQS, on peut faire l’analogie avec le son. Considérons une classe dans laquelle le professeur parle près du tableau. Il s’adresse à l’ensemble de la classe : aux premiers rangs comme aux derniers rangs.
Théoriquement, le son se propage à une vitesse finie (environ 340 m/s) donc les premier rangs entendent et réagissent (!!) aux paroles de l’enseignant avant les élèves du derniers rangs. Néanmoins, on peut considérer que la réaction des élèves se fera à peu près en même temps (ou du moins qu’elle dépend des caractéristiques propre à l’élève comme son temps de réaction et non sa position dans la classe). On considère donc dans cet exemple que le temps de propagation du son est très petit devant :
le temps du débit de parole (les records de débit sont de l’ordre d’une dizaine de mots par seconde et si le professeur parlait à cette vitesse, personne ne comprendrait… )
le temps de réaction de l’élève (… )
On peut donc considérer que l’ARQS s’applique à une conversation dans une classe.
Exercice ARQS dans un circuit de TP
Question : En suivant l’analogie précédente, estimer les fréquences acceptables pour le spectre d’un signal électrique (tension, intensité) tel qu’on puisse négliger la propagation et se placer dans l’ARQS.
Réponse : On a vu que la durée de propagation dans un circuit de TP est de l’ordre de \(10^{-9} \rm{s}\), donc tant que les temps caractéristiques associées à chaque composante spectrale sont grands devant ce temps, on peut considérer qu’on est dans l’ARQS. Soit des fréquences très inférieures à 1GHz.
Remarque : En TP, on dépassera rarement le MHz en terme de fréquence.
Exercice ARQS ou pas
On peut considérer un autre exemple où l’ARQS s’applique et … ne s’applique pas suivant ce qu’on considère : l’orage.
Considérons l’éclair, donc la propagation d’une onde lumineuse. La vitesse de la lumière dans l’air est de l’ordre de \(3 \times 10^8 \rm{m/s}\). Pour un éclair qui se produit à quelques kilomètres, le temps qu’il arrive à notre oeil est de l’ordre de \(10^{-5} \rm{s}\): ce temps est très faible devant la persistance rétinienne (\(10^{-1} \rm{s}\)). On peut donc appliquer l’ARQS et considérer que le moment où l’éclair se produit coïncide avec le moment où on le voit.
Considérons le tonnerre (qui accompagne l’éclair), donc la propagation d’une onde sonore. Cette fois, la vitesse du son est de l’ordre de \(340 \rm{m/s}\). Pour le tonnerre qui se produit à quelques kilomètres, le temps de propagation du son est de l’autre de 1 à 10 secondes. Ce temps est de l’ordre (voire plus grand) que le temps de réaction humain au son. Donc cette fois, on doit tenir compte de la propagation et on ne peut pas se placer dans l’ARQS.
Définitions utiles¶
Définitions utiles
Voici quelques éléments de vocabulaire utiles quand étudie un circuit électrique.
Fil de connexion : Un fil de connexion est un élément du circuit où tous les points ont le même potentiel.
Exemple : \(V_A = V_C = V_D\)
Conséquence : Cela réduit énormément le nombre d’inconnues.
Question : Combien y a-t-il de points de potentiel différents dans le circuit ci-contre ? Combien sont inconnu ?
Réponse : Ils y a 3 points de potentiels différents. Il y a donc 2 potentiels inconnus. En effet, le potentiel étant défini à une constante près, on peut choisir l’origine des potentiels électriques (par exemple poser \(v_E = 0\), ce choix est arbitraire).
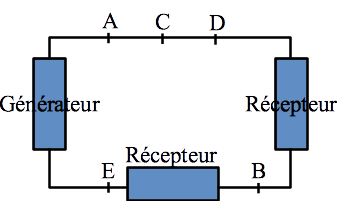
Bornes (ou pôles) : Point de potentiel reliant un composant électronique au circuit.
Dipôles : Composants électroniques composés de deux bornes. Ce seront les composants que nous étudierons principalement.
Maille : Ensemble de dipôles reliées entre eux par des fils de connexion et formant une boucle fermée.
Noeud : Un noeud est un point où se rencontrent au moins trois fils : le débit d’électrons se sépare (ou converge) donc en ce point.
Exemple : Sur le circuit ci-contre, il y a trois mailles différentes, quatre dipôles, trois points de potentiels différents et deux noeuds.
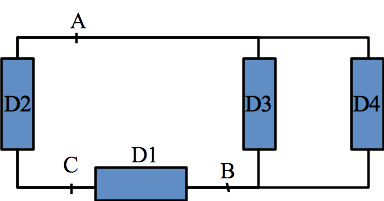
Important
Définition : Dipôles en série et en parallèle
Deux dipôles sont en série lorsqu’ils sont reliées entre eux par un fil de connexion et qu’il n’y a pas de noeud au niveau de cette liaison.
Deux dipôles sont en parallèle lorsque leurs bornes sont reliées deux à deux.
Exemple : Dipôles en série et en parallèle

Dans le circuit ci-conctre :
D1 et D2 sont en série
D1 et D3 ne sont pas série ni en parallèle (D2 et D3 non plus)
D1 et D4 ne sont pas série ni en parallèle (D2 et D4 non plus)
D3 et D4 sont en parallèle
Un ensemble de dipôles en série forme une branche.
Intensité dans une branche dans l’ARQS¶
Important
Fondamental : Intensité dans une branche dans l’ARQS
Dans l’ARQS, l’intensité est la même en tout point d’une même branche (c’est-à-dire d’un ensemble de dipôles et fils de connexion sans noeud).
Démonstration
L’ARQS suppose qu’il n’y a pas de phénomène de propagation. Une conséquence est l’absence de phénomène d’accumulation de charge en un point (car sinon cela produirait un phénomène de rééquilibrage et donc une réponse du circuit différente en chaque point).
Cela signifie que pour une portion de fil, le débit de charge entrant (l’intensité en entrée) égale le débit de charge sortant (l’intensité en sortie). Comme on peut prendre n’importe quelle portion de fil, il vient que l’intensité est la même en tout point du fil et par extension en tout point d’une branche.
Exercice

Dans ce circuit en ARQS, il y a donc :
2 potentiels inconnus (ou trois tensions à déterminer)
3 intensités inconnues puisqu’il y a 3 branches
Il reste à déterminer des équations reliant les différentes grandeurs (il en faut donc 5/6 a priori - à moins qu’on connaisse par hypothèse certaines de ces grandeurs) pour pouvoir résoudre le circuit, c’est-à-dire déterminer toutes les grandeurs. On distinguera deux types d’équations :
les équations qui relient les grandeurs de mêmes types (tensions/potentiel ou intensité). Ce seront les lois fondamentales de l’électrocinétique : les lois de Kirchhoff.
les équations qui relient l’intensité qui circule dans un dipôle à la tension à ses bornes. On parle d’équation d’évolution d’un dipôles. Elles sont propres à un type de dipôle (source de tension, résistance, bobine… ) et seront traitées dans le chapitre suivant.
- 1
Expérience de Millikan —La quantification de la charge a été observée par Millikan (1909) en étudiant la suspension de gouttes d’huile sous l’effet d’un champ électrostatique.
- 2
Origine du champ électrique —Dans un circuit électrique, une source (pile ou générateur) créé un champ électrique. Le lien entre la source et le champ électrique crée est très complexe et sa compréhension n’est pas nécessaire ici.