Etude d’un circuit linéaire¶
Méthode: Etudier un circuit électrique linéaire¶
Le but de cet exercice est d’apprendre à mettre en application tout ce qui a été vu précédemment. Nous utiliserons ici la loi des noeuds en terme de potentiel. On pourra néanmoins s’entraîner à reprendre l’exercice en utilisant des tensions et la loi des mailles.
Exercice
On considère le circuit ci-dessous. Déterminer l’intensité i circulant dans la résistance \(R_1\).
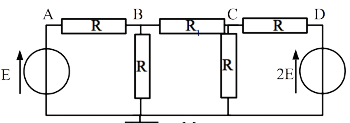
Correction
Comme d’habitude, on commence par paramétrer le système. On a au passage choisi une référence des potentiels (masse) au point M puisqu’on compte utiliser la loi des noeuds en terme de potentiel.
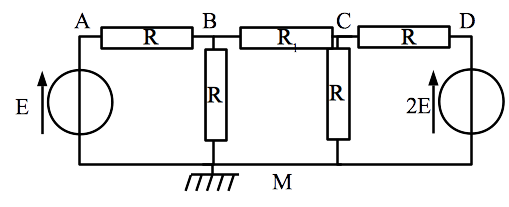
On sait déjà que \(V_A = E\) et \(V_D = 2E\)
Les lois des noeuds aux points B et C (s’entraîner à les établir impérativement) s’écrivent:
Résolution du système.
Ici, on doit chercher \(V_C\) et \(V_B\) puisque l’intensité recherché s’écrit \(\frac{V_B - V_C}{R_1}\). Réorganisons le système pour le résoudre.
soit en résolvant le système (s’entraîner impérativement à le faire):
d’où une intensité:
Vérification du résultat
Homogénéité: On a bien une tension sur une résistance, soit une intensité.
Sens physique: Les résistances étant symétriques, seules les fem sont différentes. Comme celle de droite est plus grande, on attend une intensité au centre qui est positive de droite à gauche. D’où le signe -.
Pont diviseur de tension¶
Important
Fondamental : Pont diviseur de tension
Considérons N résistances en série dont les résistances sont \(\{R_i \vert i \in [\![1;n]\!]\}\) aux bornes de laquelle la tension est u.
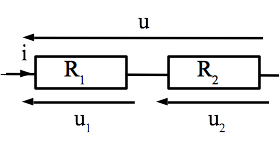
L’intensité circulant dans l’ensemble est:
Et la tension u se divise dans chaque dipôle. La tension aux bornes de la résistance \(R_k\) est:
Démonstration
On peut utiliser l’additivité des tensions: \(u = \sum_{i=1}^{i=n} u_k = \sum_{i=1}^{i=n} R_k i = \) d’où l’expression de l’intensité.
De \(u_k = R_k i\), on obtient l’expression de la tension.
Pont diviseur de courant¶
Important
Fondamental : Pont diviseur de courant Considérons N résistances en parallèle dont les conductances sont \(\{G_i \vert i \in [\![1;n]\!]\}\) dans laquelle entre une intensité totale i.
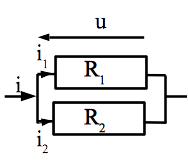
La tension aux bornes de l’ensemble est:
Et le courant i se divise dans chaque branche. L’intensité aux bornes de la résistance \(R_k\) est:
Démonstration
On peut écrire une loi des noeuds: \(i = \sum_{i=1}^{i=n} i_k = \sum_{i=1}^{i=n} G_k u = \) d’où l’expression de la tension.
De \(i_k = G_k u\), on obtient l’expression de l’intensité.
Méthode: Repérer et utiliser un pont diviseur de tension¶
Le but de cet exercice est d’apprendre à utiliser un pont diviseur de tension. La méthode peut s’appliquer aussi au cas d’un pont diviseur de courant.
Exercice
Déterminer la condition reliant les résistance pour que la tension \(U_{AB}\) soit nulle (on dit que le pont est alors équilibré).
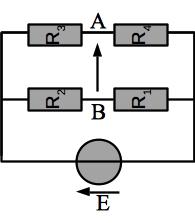
Fig. 14 Pont de Wheatstone¶
Correction
Analyse du problème.
La grandeur qu’on doit exprimer est ici la tension \(U_{AB}\). On doit l’exprimer en fonction des grandeurs connues à savoir les résistances et E.
Il n’y a pas obligation d’utiliser un pont diviseur de tension mais le but est ici de montrer comment on l’applique.
On a (on a orienté toutes les tensions \(U_{Ri}\) de la droite vers la gauche comme E) : \(U_{AB} = U_{R4} - U_{R1}\). C’est pour calculer ces deux tensions qu’on peut utiliser des ponts diviseurs de tension.
Application d’un pont diviseur de tension.
On doit :
Repérer les résistances qui sont en série et repérer la tension au bornes du pont.
Repérer la résistance dont on veut déterminer la tension et appliquer la formule du pont diviseur de tension. Attention à l’orientation des tensions car la tensions \(U_k\) doit être orientée dans le même sens que la tension globale (ici E) pour appliquer la formule du pont.
Les résistance \(R_1\) et \(R_2\) sont en série : elles forment un pont diviseur de tension dont la tension aux bornes est E. Cela nous permet de calculer \(U_{R1}\):
Les résistance \(R_3\) et \(R_4\) sont en série : elles forment un pont diviseur de tension dont la tension aux bornes est E. Cela nous permet de calculer \(U_{R4}\):
Équilibre du pont
Il vient :
Le pont est donc équilibré quand :
Modélisation des appareils complexes : Résistance d’entrée et résistance de sortie¶
Important
Fondamental : Résistance d’entrée d’un instrument de mesure Un instrument de mesure comme un multimètre ou un oscilloscope possède ses propres caractéristiques électriques. Du point de vue du reste du circuit, ce comportement, en régime indépendant du temps, peut-être modélisé par une résistance qu’on appelle résistance d’entrée de l’appareil.
Important
Fondamental : Résistance de sortie d’un générateur, d’une source Lorsqu’on utilise un générateur (GBF comme générateur basse fréquence en TP) en pratique, on règle la tension qu’il doit délivrer. Cela revient à régler la fem de la source étudiée précédemment. Néanmoins, dans une source réelle, l’intensité demandée occasionne une chute de tension qu’on modélise par une résistance en série avec la fem (modèle de Thévenin). Cette résistance est appelée résistance de sortie du générateur.
Influence de la résistance d’entrée et de sortie
Comme tout dipôle électrique, la résistance d’entrée d’un voltmètre ou d’un oscilloscope et la résistance de sortie d’un générateur influe sur le reste du circuit. Nous allons voir dans l’exercice à venir quelle propriété doit avoir une résistance de sortie ou une résistance d’entrée pour perturber le circuit le moins possible.
D’un point de vue pratique, on peut retenir que si la tension de sortie du GBF n’est pas la tension réglée sur le GBF, c’est probablement que la résistance de sortie du GBF influe sur le circuit de manière non négligeable.
Exercice Résistance de sortie d’un GBF
La résistance de sortie d’un GBF est une donnée constructeur. Elle peut être affichée sur la face avant du générateur (comme sur la photo suivante), ou donnée dans une notice ou encore réglable.

Attention
C’est une modélisation
On rappelle que la constitution réelle d’un générateur et d’un oscilloscope est bien plus complexe que ne laisse penser sa modélisation. Il s’agit simplement ici de proposer un schéma électrique __simple __correspondant au comportement intensité-tension du dipôle.
Autrement dit, vu du reste du circuit, le dipôle se comporte comme…
Complément : Résistance et impédance
En régime variable, le comportement d’un oscilloscope (ou d’un GBF) n’est plus tout à assimilable à une résistance seule. Une modélisation plus complète utilise des condensateurs voire des bobines. L’ensemble est alors appelée impédance d’entrée (ou de sortie pour un GBF).
La nécessité d’améliorer la modélisation dépend des conditions d’utilisation mais c’est la raison pour laquelle, on trouvera en général le terme d’impédance dans les notices et non de résistance (même si l’unité est toujours des \(\Omega\)).
Complément : Les quadripôles
Comme leur non l’indique, les quadripôles sont des composants électroniques possédant 4 bornes. Ils sont en général utilisé comme des dispositifs entrée-sortie : ils reçoivent une tension (d’entrée) sur deux de leur bornes (bornes d’entrée) et fournissent une tension (de sortie) sur les deux autres bornes (bornes de sortie).
Un exemple de quadripôle très fréquent est l’amplificateur : son rôle est de recevoir une tension d’entrée \(U_e\) et de fournir en sortie une tension \(U_s = K U_e\) multiple du signal d’entrée (il s’agit d’un modèle simple de l’amplificateur dont le comportement réel peut-être plus complexe).
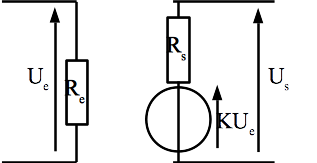
Un amplificateur est en général un dispositif relativement complexe (il nécessite souvent des transistors et une alimentation auxiliaire) mais du point de vue des circuits auxquels il est branché (circuit d’entrée (ou primaire) qui fournit \(U_e\) et circuit de sortie (ou secondaire) qui reçoit la tension \(U_s\) amplifiée) comme :
une résistance (ou plus généralement impédance) d’entrée pour le circuit primaire
un modèle de Thévenin composée d’une fem \(K U_e\) et d’une résistance (ou plus généralement impédance) de sortie pour le circuit secondaire
Ainsi, et malgré la complexité du montage réel, l’amplificateur peut être modélisé dans le circuit sous la forme du circuit ci-contre.
Remarque : On dit que la source \(K U_e\) est une source liée car sa fem est liée au reste du circuit.

Fig. 15 Amplificateur (en rouge : l’entrée, en vert : la sortie)¶
Utilisation des ponts diviseurs pour étudier l’influence des résistances d’entrée et de sortie.¶
Le but est autant d’apprendre à utiliser les ponts diviseurs que d’observer théoriquement l’influence des résistances d’entrée et de sortie et d’en déduire les valeurs optimales de ces grandeurs.
Dans les deux exercices posés ici, les circuits ne sont pas dessinés. Il est vivement conseillé de s’entraîner à les dessiner.
Exercice
On considère un circuit constitué d’un générateur modélisé par la représentation de Thévenin \((E ;R_S)\) et d’une résistance R. L’utilisateur règle sur le générateur la tension E et attend normalement que la tension aux bornes de R soit celle qu’il a réglé.
Exprimer la tension aux bornes \(u_R\) de la résistance R. L’utilisateur obtient ce qu’il attend en toute rigueur.
A quelle condition peut-on considérer que \(u_R \approx E\) ? En déduire la condition que doit vérifier une impédance de sortie pour ne pas influer sur le circuit.
Méthode de la tension de moitié : Si l’on suppose que R est variable, pour quelle valeur de R, la tension \(u_R\) vaudra E/2 ?
Correction
Q1.
R et \(R_S\) sont en série, elles forment un pont diviseur de tension dont la tension aux bornes est E. Il vient que : \(\boxed{u_R = \frac{R}{R + R_S} E}\)
Q2.
Il faut que \(\frac{R}{R+R_S} \approx 1\) soit \(\boxed{R_S << R}\)
Important
Fondamental : Choix de la résistance de sortie
Pour qu’un GBF influe peu sur le circuit, il faut que sa résistance de sortie soit très faible devant les résistances du circuit.
Si cette condition n’est pas réalisée, la tension à la sortie du GBF ne sera pas la tension réglée (sa fem) mais elle sera plus faible.
Q3.
Il vient immédiatement \(R = R_S\). Cette observation permet de mesurer \(R_S\). C’est ce qu’on appelle la méthode de la tension de moitié.
Exercice
On considère une résistance R dont on veut connaître la tension à ses bornes. On branche un voltmètre de résistance d’entrée \(R_e\) en parallèle de R pour mesurer sa tension.
Quelle la résistance équivalente \(R_{eq}\) de l’ensemble des deux résistances ?
On peut considérer que le circuit n’est pas influencé par le voltmètre si la résistance équivalente est à peu près égale à R. A quelle condition sur \(R_e\), cette approximation est valable. En déduire les bonnes caractéristiques d’une résistance d’entrée pour un voltmètre.
On ne place pas dans l’approximation précédente et une intensité i arrive sur l’ensemble résistance+voltmètre. Quelle est la chute d’intensité \(\Delta i = i - i_R\) avec \(i_R\) l’intensité circulant dans la résistance ?
Correction
Q1.
On a deux résistances en parallèle donc : \(\boxed{R_{eq} = \frac{R R_e}{R_e + R}}\)
Q2.
On veut \(\frac{R_e}{R_e+R} \approx 1\) soit \(\boxed{R_e >> R}\).
Important
Fondamental : Choix de la résistance d’entrée
Pour qu’un voltmètre influe peu sur un circuit, il faut que son impédance d’entrée soit grande devant les impédances du circuit.
Attention
Cas d’un ampèremètre
Pour un ampèremètre, la résistance d’entrée doit au contraire être très faible.
Q3.
On a un pont diviseur de courant entre R et \(R_e\) et la chute d’intensité correspond à l’intensité qui circule (loi des noeuds) dans le voltmètre. Il vient :
\(\boxed{\Delta i = \frac{\frac{1}{R_e}}{\frac{1}{R}+\frac{1}{R_e}} i = \frac{R}{R_e+R} i}\)
On retrouve le fait que plus \(R_e\) est grande, plus la chute d’intensité sera négligeable devant i.