Dipôles linéaires passifs¶
Résistance ou conducteur ohmique¶
Description physique
Tout conducteur dissipe de l’énergie par effet Joule (dissipation de l’énergie des électrons par interaction désordonnée avec le cristal du conducteur). Dans une résistance, on cherche à contrôler et augmenter cet effet (qui est très faible voire négligeable dans un fil de connexion).
Important
Définition : Résistance ou conducteur ohmique
Un conducteur ohmique ou résistance est un dipôle dont l’équation d’évolution est en convention récepteur:
où R est appelée résistance. Son inverse \(G = 1 / R\) est appelée conductance
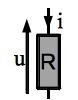
Fig. 9 Schéma d’une résistance¶
Condensateur¶
Description physique d’un condensateur
Une capacitance ou un condensateur est un dipôle construit de la manière suivant: deux conducteurs (des plans, des cylindres… ) se font face. Entre les deux, un isolant empêchent le passage des électrons.
Quand les électrons sont mis en mouvement, ils vont se détacher d’un conducteur (qui se charge positivement) et s’accumuler sur l’autre (qui se charge négativement): la différence de charge créé un champ électrique qui peut mettre en mouvement les charges dans l’autre sens: on crée temporairement une source d’énergie qui peut se décharger dans d’autres dipôles.
Important
Définition : Condensateur et capacité
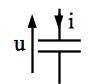
Fig. 10 Schéma d’un condensateur¶
Un condensateur (ou capacitance) est un dipôle linéaire passif constitué de deux armatures métalliques dont l’équation d’évolution est:
\(q(t) = C u(t)\)
où q(t) est la chargée portée par l’armature où pointe la flèche de la tension u(t).
C est appelée capacité du condensateur.
Important
Fondamental : Relation intensité-tension
En convention récepteur, l’équation d’évolution s’écrit aussi:
Démonstration
Il suffit de remarque que la quantité de charge ajoutée dq à l’armature où entre l’intensité pendant un temps dt est la quantité de charge qui a transité dans le fil durant le même temps dt (conservation de la charge et ARQS) soit \(i(t) = \frac{dq}{dt}(t) = C \frac{du}{dt}(t)\)
Remarque
Caractéristique statique
La caractéristique statique d’un condensateur est la droite horizontale i = 0.
Le condensateur est donc assimilable à un interrupteur ouvert en régime indépendant du temps.
Bobine idéale et inductance¶
Description physique d’une bobine
Une bobine est un dipôle dont le fonctionnement est basé sur le phénomène d’induction: un champ magnétique variable engendre un champ électrique. Dans le cas d’une bobine, on enroule beaucoup de fil pour former des spires. L’intensité qui traverse ces spires crée un champ magnétique et si l’intensité est variable, le champ magnétique aussi. Il naît alors une tension aux bornes des spires.
Important
Définition : Bobine ou inductance
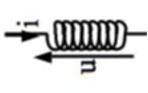
Fig. 11 Schéma d’une bobine¶
Une inductance (ou bobine) est un dipôle dont l’équation d’évolution en convention récepteur est:
Remarque
Caractéristique statique
La caractéristique statique d’une bobine est une droite d’équation u(t) = 0
En régime indépendant du temps, une bobine est donc assimilable à un fil.
Complément : Bobine réelle

Dans les bobines, la longueur des fils et l’utilisation de noyau de fer implique des effets résistifs.
On modélise ces effets par une résistance en série avec l’inductance. On trouvera quelque fois une référence à cette modélisation par une valeur de résistance associée à la valeur de l’inductance.
Puissance perdu par effet Joule¶
Effet Joule
Dans une résistance, la puissance reçue est toujours positive: \(p(t) = R i^2(t) = \frac{u^2(t)}{R}\).
Cette puissance est irrémédiablement perdue par le circuit. On parle d’effet Joule.
Utilisation et problèmes
L’effet Joule est autant un problème qu’un intérêt. Dans les chauffages électriques par exemple, il est le principe même de fonctionnement du système.
A l’inverse, dans de nombreux dispositifs électroniques, les résistances sont utilisées pour contrôler les caractéristiques du circuit et l’effet Joule est une effet supplémentaire non voulu qui tend à chauffer les composants au risque de les dégrader.
Energie stockée dans une bobine ou condensateur¶
Important
Fondamental : Energie stockée dans un condensateur
Lorsqu’on applique une tension u à ses bornes, un condensateur stocke une énergie :
Fondamental : Energie stockée dans une bobine
Lorsqu’un courant i circule dans une bobine, celle-ci stocke une énergie :
Justification
Nous allons montrer que la puissance reçue par la bobine et le condensateur peut se mettre sous la forme \(P = \frac{dE}{dt}\). On observe ainsi qu’on peut exprimer la puissance échangée comme une variation d’énergie. Celle-ci correspondra à la variation d’énergie du dipôle.
La puissance reçue par un condensateur s’écrit (on l’oriente en convention récepteur):
(on a cherche une primitive à la fonction u(t) u’(t)).
La puissance reçue par une bobine s’écrit (on l’oriente en convention récepteur):
(on a cherche une primitive à la fonction i(t) i’(t)).
On trouve bien les expressions des deux énergies données précédemment.
Différence entre effet Joule et énergie stockée
Il est important de comprendre la différence de traitement entre la résistance et le condensateur (la bobine). Dans le premier cas, l’énergie est perdue et ne peut plus être récupérée par le même processus physique. Dans le cas du condensateur (de la bobine), l’énergie est stockée est peut-être redonnée au circuit.
On pourra faire une analogie avec la différence entre l’énergie perdue par frottements et l’énergie stockée (ou rendue) sous forme d’énergie potentielle de pesanteur.