Entrainement : Systèmes centrés#

Ces exercices seront traités en classe.

Le sextant#

Le sextant est un appareil qui était utilisé par les marins pour déterminer la latitude. Pour cela, il mesurait la hauteur d’un astre (Soleil,Lune… ) au dessus de l’horizon. Le sextant est composé de deux miroirs plans M1 et M2 (ce dernier étant semi-réfléchissant) et d’une lunette de visée (que nous n’étudierons pas ici). La direction OC du plan du miroir pointe un repère sur l’arc de cercle gradué AB qui mesure 60∘. Sur la figure, les proportions ne sont pas respectées.

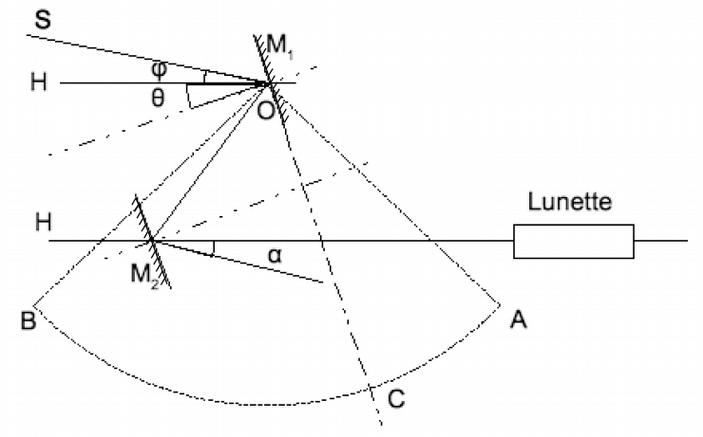
../_images/sextant.jpg

Fig. 11 Sextant#

Avec la lunette, l’observateur vise l’horizon donc l’axe optique de la lunette a la direction horizontale. La normale au plan du miroir M2 est fixe et fait un angle de 30∘. Ce miroir est aussi parallèle à la direction OA où O est le point d’incidence des rayons de l’astre sur le miroir M1 (qu’on peut assimiler au “centre” du miroir plan M1). On note θ l’angle entre la normale à M1 et l’horizontale et ϕ celui de la direction de l’astre par rapport à l’horizontale. On les considère positifs dans la configuration donnée sur le schéma.

Exercice

  1. Déterminer en fonction de ϕ et θ, l’angle α que fait le rayon réfléchi sur M2 avec l’horizontale.

  2. Quel doit-être l’angle θ pour que le rayon réfléchi sur M2 soit selon l’axe optique de la lunette?

  3. Dans ces conditions, déterminer la relation entre l’angle AOC et l’angle SOH où S désigne la position de l’astre et H l’horizon.

Point utile pour cet exercice

Dioptre hémisphérique#

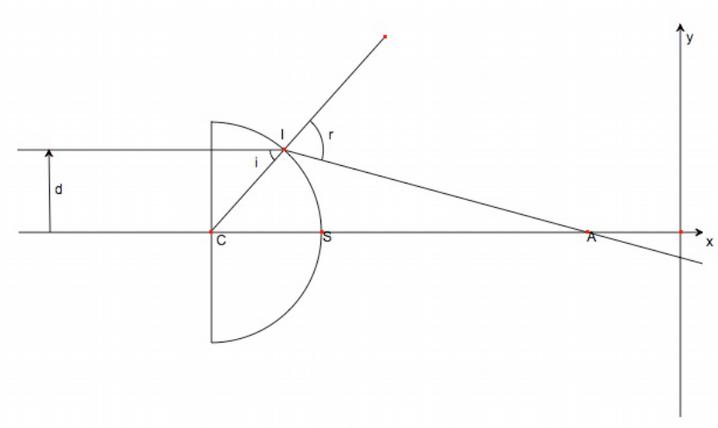
On étudie un dioptre hémisphérique (une lentille) de rayon R et d’indice n plongé dans l’air d’indice 1. On s’intéresse aux phénomène d’aberration. Un faisceau cylindrique (de rayon dmax) de lumière monochromatique arrive sous incidence normale sur la lentille; ce faisceau est donc issu d’un point objet B situé à l’infini dans la direction de l’axe.

../_images/dioptre_hemispherique.jpg

Exercice

  1. On considère un rayon du faisceau de lumière à une distance d de l’axe optique. Établir la relation donnant CA en fonction de R = CS, et des angles i et r.

  2. Montrer que quand on se place dans l’approximation de Gauss (d≪R), on peut considérer que tous les rayons coupent l’axe optique en un même point F’ dont on déterminer la distance à C. F’ est donc l’image de B dans les conditions de Gauss.

  3. Comment appelle-t-on F’?

  4. On n’est plus dans les conditions de Gauss. Quelle est la valeur d0 limite de d max du faisceau incident si l’on veut que tous les rayons du faisceau incident ressortent de la lentille?

  5. Faire l’application numérique pour n = 1,5, R = 5cm.

  6. *Faire un développement limité au second ordre en i de la distance CA. Conclure quant à la possibilité de réaliser l’approximation de Gauss.

Point utile pour cet exercice