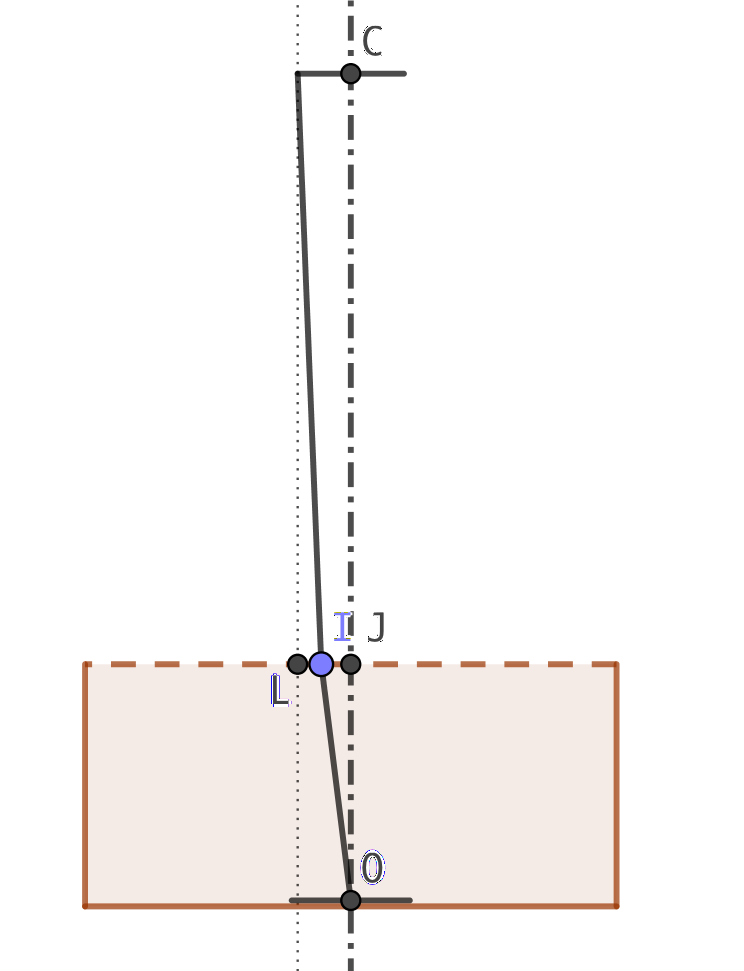
Mise en équation
Notons le point I, le point d’incidence sur le dioptre air-eau pour le rayon extrême du faisceau issu de O et entrant dans la pupille. On note \(i_1\) et \(i_2\) les angles respectivement d’incidence et de réfraction. On a les relations :
\[\begin{align*}
n_{eau} \sin i_1 &= n_{air} \sin i_2\\
\frac{IL}{\tan i_2} &= H_1\\
IL + IJ &= R_1\\
\tan i_1 &= \frac{IJ}{H_0}
\end{align*}\]
On a 4 inconnues (IL, IJ, \(i_1\) et \(i_2\)) et quatre inconnues, on peut donc résoudre le système.
Il est important de voir que la résolution complète ne nous intéresse pas. On veut \(i_1\) qui représente l’ouverture angulaire. On va donc chercher à garder \(i_1\) et éliminer les autres inconnues.
Les grandeurs \(H_0, H_1, R_1\) et les indices sont des grandeurs connues qu’on va garder.
Equation pour l’angle:
Les deux dernières équations permettent d’écrire: \(IJ = H_0 \tan i_1\) et \( IL = R_1 - H_0 \tan i_1\) d’où le système:
\[\begin{align*}
n_{eau} \sin i_1 &= n_{air} \sin i_2\\
\frac{R_1}{\tan i_2} - H_0 \frac{\tan i_1}{\tan i_2}&= H_1
\end{align*}\]
soit en éliminant \(i_2\) (on a directement utilisant \(n_{air} = 1\) - on peut se le permettre car l’indice de réfraction est sans dimension: le changer par sa valeur numérique n’impacte pas l’analyse dimensionnelle):
(1)\[\begin{equation}
\left ( R_1 - H_0 \tan i_1 \right )\sqrt{1 - n_{eau}^2 \sin^2 i_1} = H_1 n_{eau} \sin i_1
\end{equation}\]
On rappelle que \(\theta_0 = i_1\)
Résolution aux petits angles
Nous allons faire une approximation pour résoudre cette équation (sans quoi la résolution devient TRÈS délicate). En effet, la taille de la pupille est de l’ordre du mm (on prendra \(R_1 = 1\rm{mm}\)) et la hauteur de la casserole est de l’ordre de la dizaine de cm. (on prendre \(R_0 = 5\rm{cm}\)). Il vient que les angles à la normale seront nécessairement petit.
On peut avoir un ordre de grandeur en considérant que \(\theta_0 \sim \arctan\frac{R_0}{2H_0} \sim 10^{-2} \rm{rad}\). En pratique, la propagation n’est pas rectiligne mais les angles \(i_1\) et \(i_2\) sont nécessairement du même ordre de grandeur que \(\theta_0\).
Or si \(\theta_0 << 1\), on peut faire les approximations dites des petits angles :
\[\begin{align*}
\sin i &\approx i\\
\tan i &\approx i\\
\cos i &\approx 1\\
\end{align*}\]
On ne conservera pas aussi les puissances au carré des petits angles (on parle d’approximation à l’ordre 1), des précisions seront données sur cette approximation dans des cours ultérieurs. On essaiera déjà d’appréhender la méthode d’utilisation de cette approximation.
Ici l’équation devient :
(2)\[\begin{equation}
\left ( R_1 - H_0 i_1 \right ) = H_1 n_{eau} i_1 \Longrightarrow \theta_0 = i_1 \approx \frac{R_1}{H_0 + H_1} = 10^{-2} \rm{rad}
\end{equation}\]